Чем меньше мощность, тем меньше передатчик, меньше потребляемая энергия источника питания, тем он дешевле.

PошДАМ=1-F(h0/2^1/2)

РошДЧМ=1-F(h0)

РошДФМ=1-F(h0*2^1/2)

Билет 5

1. Передаточная характеристика ЦФ.

ЦФ – это микроЭВМ, которая решает задачу фильтрации средствами вычислительной техники. Описывается разностным уравнением, которое является цифровым эквивалентом аналогового дифференциального уравнения: y_i==∑^L_l=1 a_ly_i-l+=∑^M_m=0 b_mx_i-m. Максимум из L,M определяет порядок фильтра.

Передаточная характеристика ЦФ. Передаточной характеристикой ЦФ k(z) называется отношение z-преобразования выходного процесса y(z) к z-преобразованию входного процесса x(z) K(z)=Y(z)/X(z)

z-преобразование процесса можно записать через его дискретные отсчеты. Пусть дано:x0,x1,x2…тогда x(z)=∑x_kz^-k

z- преобразования это z=exp(jwT_д)=coswT_д+jsinwT_д

Передаточная функция ЦФ 2-го порядка равна:

K(Z)=Y(Z)/X(Z)=b₀+b₁z^-1+b₂z^-2/1-a₁z^-1-a₂ z^-2

До множить на z² тогда K(Z)=Y(Z)/X(Z)= b₀z²+b₁z^-+b₂/z²-a₁z^--a₂

ЦФ называется устойчивым, если при ограниченном воздействии на входе xi<∞ напряжение на выходе также ограничено yi<∞ .

Необходимое и достаточное условие ЦФ является ∑|gi|<∞

Полюса передаточной функции ZP_1,2= (a₁+(-)√a₁²+4a₂ )/2

Цифровой фильтр устойчив, если корни по модулю | ZP_1,2|<1

Также можно получить выражения для АЧХ и ФЧХ фильтра:

АЧХ: |K(jwTд)|=√(Re K1(jwTд))²+(Im K1(jwTд))²/( Re K2(jwTд))²+(Im K2(jwTд))²

ФЧХ: φ(jwTд)=arctg(Im K1(jwTд)/ Re K1(jwTд))-arctg(Im K2(jwTд)/ Re K2(jwTд))

Расчет напряжения на выходе ЦФ. (дискретная свертка)

y(t)=∫x(τ)*y(t-τ)dτ

Для цифрового фильтра ЦФ непрерывное время t заменяется на дискретная время t→i

Интеграл от (0 до Т) заменяется на сумму ∑; Переменная интегрирования τ меняется на k

Цифровая свертка равна y_i =∑x_kg_i-k

2. Помехоустойчивость оптимального приемника.

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью.

Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость

Количественная мера помехоустойчивости называется вероятность ошибки p

---

.

P=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок не верно принятых сообщений )

Высокая помехоустойчивость соответствует маленькой вероятности ошибки, низкая помехоустойчивость соответствует большой вероятности ошибки. Потенциальная помехоустойчивость соответствует минимальной вероятности.

Система связи работает с такими вероятностями: P=10^-1−10^-3 удовл.качество

P=10^-4−10^-6 хорошее качество (используют для передачи речи); P=10^-7−10^-9 отличное.

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Правило работы оптимального приемника может быть только статистическим.

если р(1/z)>p(0/z) решение R=1

если р(1/z)

Пусть в линии связи действует единственная помеха (АБГШ), со спектральной плотность G₀, тогда сравнение условной вероятностей эквивалентно следующему сравнению:

∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1; ∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0

Физическая сущность "0" и "1" зависит от вида модуляции.

1)Двоичная амплитудная модуляция(ДАМ)

U1(t)=UmCosw0t

U0(t)=0

2)Двоичная частотная модуляция(ДЧМ)

U1(t)=UmCosw1t

U0(t)=UmCosw0t

3)Двоичная фазовая модуляция(ДФМ)

U1(t)=UmSinw0t

U0(t)=-UmSinw0t

Полной характеристикой помехоустойчивости является полная вероятность

P=p(1)p(0/1)+p(0)p(1/0)

P(1)=p(0)=0.5 рассчитаем прием 1 при передаче 0

Расчетам вероятность приема 1 при передачи 0: p(1/0)=p{[z(t)-U₁(t)]²dt<[z(t)-U₀(t)]²}=(но мы передавали ноль т.е z(t)=U₀(t)+x(t))=p{[∫x²(t)+2x(t)[U₀(t)-U₁(t)]+[ U₀(t)-U₁(t)]² dt<∫ x²(t)dt} = p{y<-0.5Ep} где Ep= ∫[U₀(t)-U₁(t)]²dt ; y=∫x(t)[U₀(t)-U₁(t)]dt

Билет 6

1.   1   2   3   4   5

---

Оптимальный приемник двоичных сигналов.

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью. Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость, которой соответствует минимальная вероятность ошибки р (р=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок).

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Эта минимальная вероятность ошибки может быть большой, но никакой другой приемник не даст меньшей вероятности ошибки.

р(1/z)-условная вероятность информации передачи 1 если на входе приемника процесс z(t)

р(0/z)-условная вероятность информации передачи 0 если на входе приемника процесс z(t)

Правило работы оптимального приемника может быть только статистическим.

если р(1/z)>p(0/z) решение R=1

если р(1/z)

Пусть в линии связи действует единственная помеха (АБГШ), со спектральной плотность G₀, тогда сравнение условной вероятностей эквивалентно следующему сравнению:

∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1; ∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0


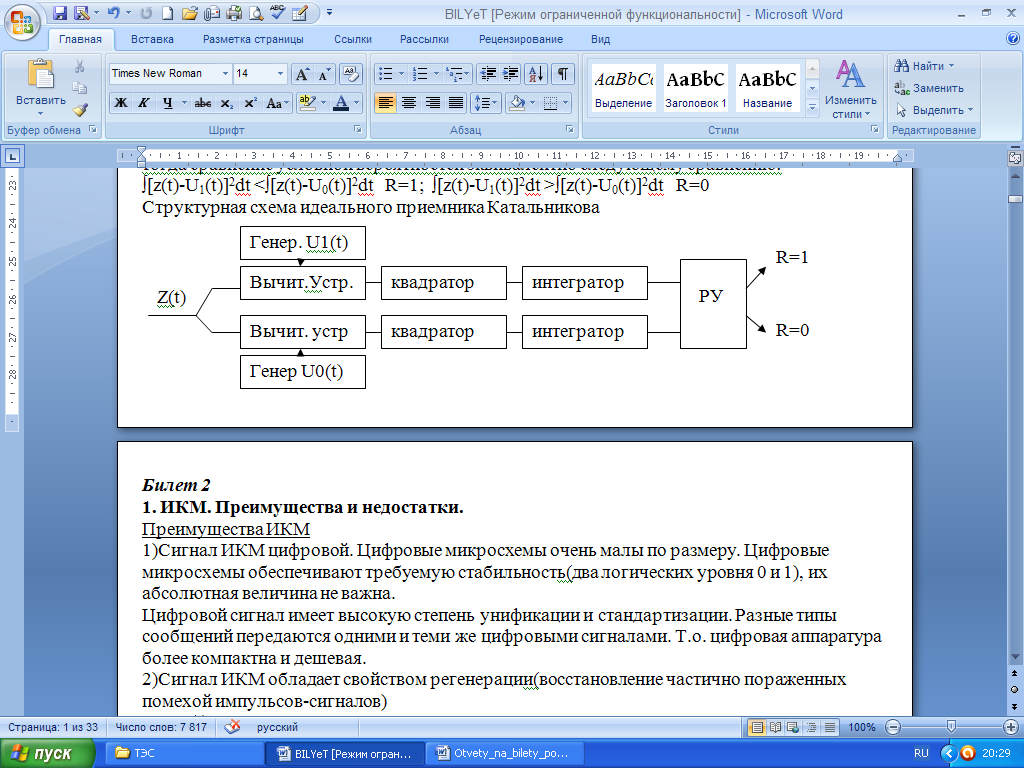
Физическая сущность "0" и "1" зависит от вида модуляции.

1)Двоичная амплитудная модуляция(ДАМ)

U1(t)=UmCosw0t

U0(t)=0

2)Двоичная частотная модуляция(ДЧМ)

U1(t)=UmCosw1t

U0(t)=UmCosw0t

3)Двоичная фазовая модуляция(ДФМ)

U1(t)=UmSinw0t

U0(t)=-UmSinw0t

2. Количество информации. Энтропия.

Количество информации, которое заключено в некотором сообщении А с вероятностью появления p(А), равно: I=-log₂p(А).Свойства количества информации:

1)чем меньше р, тем больше I (количество информации.)

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Энтропия H - это среднее кол-во информации приходящееся на одно сообщение

Для дискретного источника независимых сообщений энтропия вычисляется по формуле:

---

Т.к. сообщения принимают различные значения с разными вероятностями, то ввели понятие энтропии (это среднее количество информации приходящееся на одно сообщение):

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа)

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны

Hmax=logm

Наиболее часто используются двоичные системы связи m=2. Энтропия двочного источника вычисляется по формуле:

H(m=2)=-p(1)*logp(1)-[1-p(1)]log[1-p(1)]

Энтропия двоичного источника максимальна если p(1)=p(0)=0.5

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево". Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m

Билет 7

1. Потенциальная помехоустойчивость.

Способность системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью.

Максимально достижимая помехоустойчивость называется потенциальной помехоустойчивостью.

Количественной мерой помехоустойчивости называется вероятность ошибки

P=lim(N->∞)Nош/N

N-общее количество переданных символов, сообщений

Nош-количество ошибок, т.е. количество неверно принятых символов, сообщений

Высокой помехоустойчивости соответствует малая вероятность ошибки, низкой помехоустойчивости соответствует большая вероятность ошибки.

Потенциальной помехоустойчивости соответствует минимальная вероятность ошибки.

Система связи работает с такими вероятностями: р=10^-1−10^-3 удовл.качество

р=10^-4−10^-6 хорошее качество (используют для передачи речи); р=10^-7−10^-9 отличное.

Приемник, реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником.

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется

---

оптимальным приемником

2. Укрупнение сообщений

Энтропия – это среднее количество информации приходящееся на одно сообщение. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации. Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации при заданной бодовой скорости - количество посылок в единицу времени

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево"

Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.

Укрупнения сообщений:

Цель статистического кодирования- увеличить энтропию и увеличить скорость передачи информации.

Пример: порядок расчета энтропии источника зависимых сообщений

1. 
   Определить общее количество N независимых слов источника. N=mⁿ (m=2;n=2)
   
2. 
   Определим вероятность каждого слова: p(AM)= p(A)*p(M/A); p(MA)=p(M)*p(A/M); p(AA)=p(A)*p(A/A); p(MM)=p(M)*p(M/M)
   
3. 
   Т.к. энтропия независимы то энтропия источника «на слово» найдем по формуле:
   

Нсл= −p(AM)logp(AM)-p(MA)logp(MA)-p(MM)logp(MM)-p(AA)logp(AA)= [дв.ед./слово]

4. 
   Энтропия на одну букву или символ(n=2): H=Hcл/n=0,828 [дв.ед/cимвол]; Избыточность т.е степень отличия энтропии источника от максимального значение R=(H_max-H)/H_max где H_max=log₂2=1
   
5. 
   Т.к. разных слов 4 то нужно использовать код с основание m=4, длина кодовой комбининации n=1, то общее число комбинаций N=4
   

Энтропия рассчитывает по формуле дискретного источника независимых сообщений:

Нсл= −p(1)logp(1)-p(2)logp(2)-p(3)logp(3)-p(4)logp(4)=1,659. [дв.ед./сообщение]

Таким образом увеличили энтропию в 2 раза. Определим избыточность источника, для H_max=log₂4=2; R=1-H/ H_max Избыточность осталось та же Т.о. увеличив энтропию мы не уменьшаем избыточность. Это означает, что есть возможность еще более увеличить энтропию.

Билет 8

1. Потенциальная помехоустойчивость ДАМ,ДЧМ,ДФМ.

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью

---

Смотрите также файлы

• Эссе по фильму Восхождение к праву студентки группы лпп 1412 Плаховой Дарьи.docx

• Задание Опишите правила согласования географических названий. Задание 2.docx

• Чн20Э271 Студент Е. И. Башилова москва 2022 Вопросы Укажите основные этапы эконометрического исследования.docx

• Лабораторная работа 1 по учебному курсу Экология.docx

• Задача Сформируйте инвестиционный портфель предприятия, если предприятие располагает суммой 800 д е., ожидаемая норма доходности 15%.docx