1. Регенерация сигнала ИКМ. Вероятности p(1/0),p(0/1)

Регенератор восстанавливает частично искаженные помехой импульсы 1 и 0

структурная схема:

ПФ->Отсчетные устройства->пороговое устройство

^

источник порогового напряжения

На вход ПФ поступает сигнал в сумме с АБГШ(аддитивный белый гауссовский шум) ПФ выделяет сигнал и часть шума. На выходе ПФ имеет процесс z(t)=Uc(t)+x(t)

Отсчетное устройство берет отсчеты процесса z(t) в середине посылки.

Пороговое устройство сравнивает отсчеты zg(t) с пороговым напряжением V. Если zg(t)>V, то на выходе порогового устроства 1, если zg(t)
Прием 0 вместо 1 называется пропуск цели. Вероятность приема 0 при передаче 1 => p(0/1) - условная вероятность приема 0 при передачи 1

Прием 1 вместо 0 - ложная тревога. Вероятность этого события p(1/0) - условная вероятность приема 1 при передаче 0

Вероятности p(1/0) и p(0/1) это условные вероятности. Их зависимость от порогового напряжения если поражающий сигнал нормальный и шум х(t):

p(1/0)=p(x>V)=∫^∞_V W(x)dx=1-F(V/σ) (замена x/σ=y и dx=σ dy)

p(0/1)=p(xV^-Uc_-∞ W(x)dx=F((V-Uc)/σ) (замена x/σ=y и dx=σ dy)

Пороговое напряжение, при котором средняя вероятность ошибки минимальна, называется оптимальным пороговым напряжением: Vопт=Uc/2-σ²/Uc * ln(p(1)/p(0))

2. Энтропия двоичного источника

Количество информации, которое заключено в некотором сообщении А с вероятностью появления p(А), равно: I=-log₂p(А).Свойства количества информации:

1)чем меньше р, тем больше I.

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Т.к. сообщения принимают различные значения с разными вероятностями, то ввели понятие энтропии (это среднее количество информации приходящееся на одно сообщение):

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа).

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны: Hmax=logm.

Избыточность это степень отличия энтропии от максимального значения: R=(Hmax-H)/Hmax.

Энтропия двоичного источника вычисляется по формуле:H=-p(1)*logp(1)-p(0)logp(0)

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево"

Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.

Билет 13

1. Вероятность ошибки при регенерации сигнала ИКМ.

Регенератор восстанавливает частично искаженные помехой импульсы 1 и 0

структурная схема:

ПФ->Отсчетные устройства->пороговое устройство

^

источник порогового напряжения

На вход ПФ поступает сигнал в сумме с АБГШ(аддитивный белый гауссовский шум) ПФ выделяет сигнал и часть шума. На выходе ПФ имеет процесс z(t)=Uc(t)+x(t)

Отсчетное устройство берет отсчеты процесса z(t) в середине посылки.

Пороговое устройство сравнивает отсчеты zg(t) с пороговым напряжением V. Если zg(t)>V, то на выходе порогового устроства 1, если zg(t)
Прием 0 вместо 1 называется пропуск цели. Вероятность приема 0 при передаче 1 => p(0/1) - условная вероятность приема 0 при передачи 1

П рием 1 вместо 0 - ложная тревога. Вероятность этого события p(1/0) - условная вероятность приема 1 при передаче 0

P 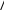(1/0)=∫1/σ√2π *exp –x²/2σ² dx (замена x/σ=y и dx=σ dy)= ∫1/σ√2π *exp –y²/2 dy σ =

1/√2π∫exp-y²/2dy=1-F(v/σ)

F(-x)=1-F(x)

P(0/1)=P([Um+x(t)])2/2σ² dx (замена x/σ=y и dx=σ dy)

=1/√2π∫exp-y²/2dy=F(V-Um/σ)

Пороговое напряжение при котором средняя вероятность ошибки P минимально называется оптимальным пороговым напряжением.

Vопт = Um/2 – σ²/Um ln p(1)/p(0)

2. Блочный код (7,3)

1)код двоичный - все комбинации состоят из 0 и 1

2)длина кода n=7 символов

3)информационных символов i=3

4)проверочных символа k=4

5)код блочный-каждому сообщению соответствует кодовая комбинация

6)код систематический-первые три символа информационные, последние четыре-проверочные(корректирующие)

Код двоичный - все комбинации состоят из 0 и 1,длина кода 7 символов, информационных 3, проверочных символа 4.

Алгоритм кодирования: присваиваем каждому значению кода номер а1,а2,а3,а4,а5,а6,а7; составляем порождающую матрицу (единичная матрица+матрица дополнение(задается)); записываем все возможные информационные комбинации и к ним все возможные проверочные символы ((а4,а5,а6,а7)=(а,а2,а3)*матрица-дополнение).

Алгоритм декодирования: составляем проверочную матрицу (транспонированная матрица-дополнение+единичная матрица); вычисляем синдром кодовой комбинации ((с1,с2,с3,с4)=(а1,а2,а3,а4,а5,а6,а7)*транспонированная-проверочная-матрица); формируем вектор ошибки (т.е. кодовую комбинацию с ошибкой) на основании синдрома.

Кодовое расстояние – количество позиций, в которых одна кодовая комбинация отличается от другой. Здесь минимальное кодовое расстояние равно 4 (т.е. код исправляет все одиночные ошибки и некоторые двойные).

Билет 14

1. Циклический код (7,4)

Код называется циклическим, если циклическая перестановка одной кодовой комбинации дает все остальные кодовые комбинации данного кода. Каждая комбинация такого кода записывается в виде полинома. Состоит из 7 символов, из которых 4 информационных и 3 проверочных.

Алгоритм формирования: записываются возможные информационные комбинации; каждую комбинацию записывают в виде полинома (а3,а2,а1,а0); выбираем образующий полином, степень которого соответствует количеству проверочных символов ; полином, соответствующий информационной комбинации, умножается на образующий полином.

Алгоритм декодирования: принятая кодовая комбинация делится на образующий полином, остаток от деления есть синдром, который указывает, где произошла ошибка; формируем вектор ошибки (т.е. кодовую комбинацию с ошибкой) на основании синдрома.

Кодовое расстояние – количество позиций, в которых одна кодовая комбинация отличается от другой. Здесь минимальное кодовое расстояние равно 3 (т.е. код исправляет все одиночные ошибки).

2. 
   Оптимальный приемник
   

Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью.

Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость

Количественная мера помехоустойчивости называется вероятность ошибки p.

P=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок не верно принятых сообщений ).

Система связи работает с такими вероятностями: P=10^-1−10^-3 удовл.качество P=10^-4−10^-6 хорошее качество (используют для передачи речи); P=10^-7−10^-9 отличное.

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Эта минимальная вероятность ошибки может быть большой, но никакой другой приемник не даст меньшей вероятности ошибки.

Правило работы оптимального приемника может быть только статистическим.

если р(1/z)>p(0/z) решение R=1

если р(1/z)

Пусть в линии связи действует единственная помеха (АБГШ), со спектральной плотность G₀, тогда сравнение условной вероятностей эквивалентно следующему сравнению:

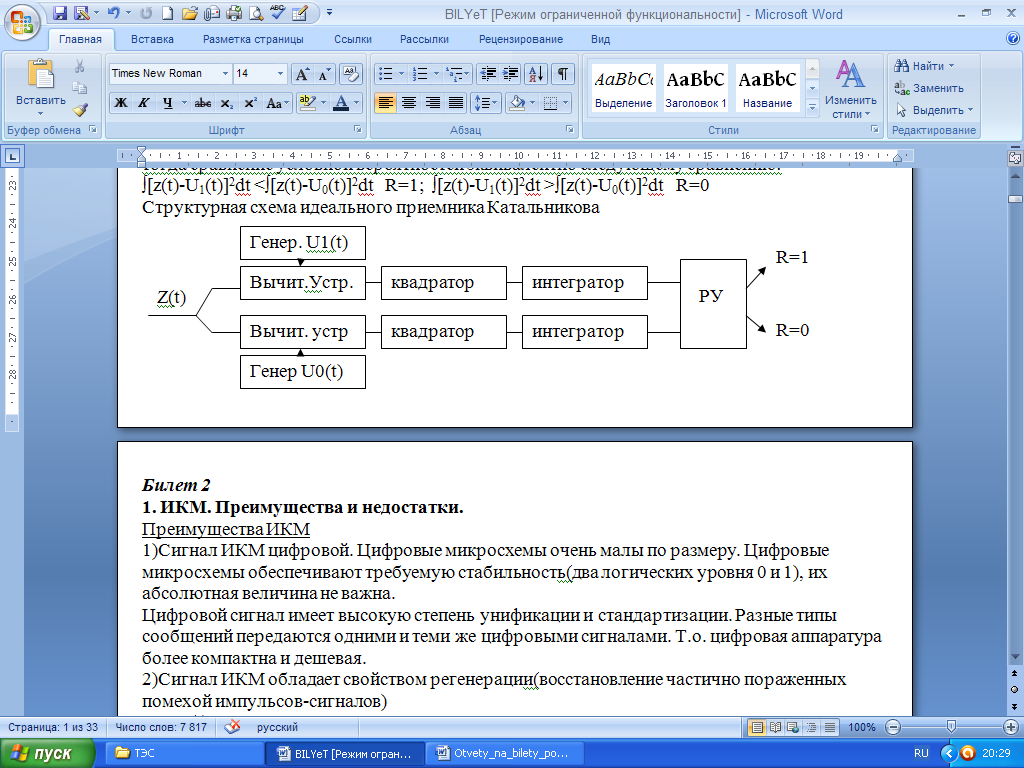
∫[z(t)-U₁(t)]²dt <∫[z(t)-U₀(t)]²dt R=1; ∫[z(t)-U₁(t)]²dt >∫[z(t)-U₀(t)]²dt R=0

Структурная схема идеального приемника Катальникова



Билет 15

1. Сверточный код

Код - двоичный (1;0)

Относится к классу непрерывных кодов (после передачи очередного кодового символа кодер не возвращается в исходное состояние, т.о. между выходными символами возникают корреляционные связи, что повышает помехоустойчивость). В общем случае сверточный кодер имеет m входов и n выходов.

Рассмотрим простейший сверточный кодер с одним входом и двумя выходами (скорость работы уменьшается в 2 раза). Принцип работы можно рассмотреть с помощью решетчатой диаграммы: при передаче 1 идем по нижнему ребру, при передаче 0 идем по верхнему ребру. Далее рассматривается в соответствии с кодовой комбинацией поступившей на вход.

2. Оптимальный приемник двоичных сигналов на СФ

Оптимальный фильтр – это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется согласованным фильтром.

Фильтр называется согласованным т.к.:

1)обеспечивает максимальное отношение с/ш на выходе: h0²=Ec/G0

2)характеристики СФ согласованы с характеристиками сигнала

а)импульсная реакция СФ совпадает с зеркальным отображением согласованного с ним сигнала

б) АЧХ СФ совпадает с амплитудным спектром сигнала(с точностью до постоянного множителя)

в)ФЧХ СФ противоположна по знаку ФЧХ сигнала

Если передаются двоичные сигналы, то оптимальный приемник содержит два согласованных фильтра (формы двоичных сигналов зависит от вида модуляции (ДАМ, ДЧМ, ДФМ)). Выражения соответствующие определенным видам модуляции позволяют сделать вывод: для ДАМ и ДФМ должен быть один СФ, а для ДЧМ – два СФ. Принцип работы – сравнивается напряжение на выходе СФ: если V1>V0, то решение 1, если V1

Билет 16

1. Теорема Шеннона

По каналу связи с полосой пропускания F, в котором действует сигнал с мощностью Pc и нормальный шум с дисперсией σ² можно передавать информацию со скоростью сколько угодно близкой к пропускной способности канала С=Flog(1+Pc/ σ²) и при этом вероятность ошибки может быть сделана сколь угодно малой.

Производительность источника – это количесвто информации, производимой источником в единицу времени: H’=H/T (H - энтропия, T – длительность сообщения).

Скорость передачи информации – количество взаиной информации передаваемой по каналу связи в единицу времени: I’=lim(I(Z,U)/T).

Пропускная способность канала вязи – максимально возможная скорость передачи информации.

Доказательство:

Количество взаимной информации содержащейся в процессе z(t) о сигнала u(t):

I(Z,U)=h(z)-h(X) (h(z), h(X) – дифференциальные энтропии соответствующих процессов).

Дифференциальная энтропия – относительная информационная содержательность непрерывного процесса (h(z)=-∫W(z)log(Wz)dz). Т.к. шум нормальный и его дисперсия σ²=G0F, то: h(X)=0.5log(2πe σ²). Чтобы энтропия процесса z была максимальной, этот процесс должен быть нормальным случайным процессом с дисперсией Рс. Тогда максимальное количество взаимной информации равно: I(Z,U)= 0.5log(2πe (σ²+Рс))- 0.5log(2πe σ²)= 0.5log(2πe(1+Рс/σ²). Т.к. процесс на выходе канала связи финитный по спектру, то полностью определяется по теореме Котельникова, т.о. в единицу времени следует передавать 2F отсчетов, тогда получаем: C=2F*I(Z,U).

2.Оптимальный приемник ДЧМ на СФ.

На базе СФ можно построить оптимальный приемник. Если передаются двоичные сигналы U1(t) и U0(T) то оптимальный приемник содержит два фильтра СФ1 согласованный с сигналом U1(t) и СФ0 согласованный с сигналом U0(t).

Сигналы U1(t) и U2(t) – это импульсы длительностью Т, форма которых зависит от вида модуляции.

О
V1
птимальный приемник двоичного сигнала с согласованным фильтром имеет вид:


CФ1

Ру

1

z(t)







СФ0

0

V2





Если напряжение V1 на выходе СФ1 больше, чем V0, то решение приемника –«1», если V1
Сигналы ДАМ и ДФМ

Должен содержать только один СФ с АЧХ равной: |К(jw)|=|(UmTsin(w-w0)T/2|

|2 (w-w0)T/2 |

Оптимальный приемник сигнала ДЧМ должен содержать два СФ:

С Ф1 с АЧХ равной: |К1(jw)|=|(UmTsin(w-w1)T/2|

| 2 (w-w1)T/2 |

С Ф0 с АЧХ равной: |К1(jw)|=|(UmTsin(w-w0)T/2|

| 2 (w-w0)T/2 |

Потенциальная помехоустойчивость такого приемника совпадает с помехоустойчивостью оптимального приемника .
Билет 17

1. ЧРК

Информация отдельных каналов передается одновременно, но в разных полосах частот (частотное разделение каналов). Разделение каналов осуществляется с помощью ПФ. Информация каждого канала передается на своей несущей

Важной характеристикой системы связи с ЧРК является групповой спектр. При однополосной АМ в канал связи передается остаток от несущей (пилот-сигнал) и боковая полоса частот. Причины взаимных помех: спектры сигналов бесконечны, характеристики ПФ неидеальны. Способы уменьшения взаимных помех: улучшать характеристики ПФ, уменьшать скорость работы по каналу, вводить защитные промежутки по частоте между каналами.

2. Согласованный фильтр

Оптимальный фильтр – это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется согласованным фильтром.

Фильтр называется согласованным т.к.:

1)обеспечивает максимальное отношение с/ш на выходе: h0²=Ec/G0

2)характеристики СФ согласованы с характеристиками сигнала

а)импульсная реакция СФ совпадает с зеркальным отображением согласованного с ним сигнала

б) АЧХ СФ совпадает с амплитудным спектром сигнала(с точностью до постоянного множителя)

в)ФЧХ СФ противоположна по знаку ФЧХ сигнала

Докажем основные свойства согласованного фильтра:

Uвых(t)=∫z(τ)g(t-τ)d τ= ∫Uc(τ)g(t- τ)dτ +∫x(τ)g(t- τ)dτ – напряжение на выходе фильтра.

Напряжение полезного сигнала ∫Uc(τ)g(t- τ)dτ.

Мощность полезного сигнала [∫Uc(τ)gcф(t- τ)dτ]² (на единичном сопротивлении).

Мощность помехи (дисперсия)

[∫x(τ)g(t- τ)dτ]²=∫x(τ)g(t- τ)dτ*∫x(V)g(t- V)dV=G₀∫б(τ-V)g(t-τ)dτ∫ g(t-V)dV=G0∫ g²(t-V)dV

Где В(τ-v)= x(τ)x(V)=G₀ δ (τ-V)

Используем фильтрующие свойства δ-функции

∫ δ (τ-V)y(t)dt=y(τ) то есть ∫ δ (τ-V)g(t-τ)dτ= g(t-V)

Отношение сигнал и шум:

Pc/σ²=[∫Uc(τ)g(t- τ)dτ]²/ G₀∫ g²(t-V)dV≤ ∫U²c(τ)g²(t- τ)dτ / G₀∫ g²(t-V)dV≤ ∫ U²c(τ)dτ/ G₀

Поскольку подынтегральное выражение не отрицательно, то интеграл будет максимален. Согласованный фильтр дает на выходе в момент времени t=T максимальное отношение сигнал шум, равный h0=∫ U²c(τ)dτ/ G₀=Ec/G0 где Ес- энергия сигнала.


Билет 18

1. ВРК

При ВРК каналы передаются в одной и той же полосе частот, но в разные интервалы времени. Каждый канал передается в свой временной интервал.

. Переносчиком информации является периодическая последовательность импульсов поступающих от генератора тактовых импульсов. Разделение каналов осуществляется с помощью коммутаторов. Коммутатор передатчика и коммутатор приемника работают синхронно. Передача осуществляется в соответствии с теоремой Котельникова. Для восстановления из импульсов-отсчетов исходного сигнала их подают на ФНЧ. Причины взаимных помех: полоса частот ограничена, импульсы могут занять соседний временной интервал; коммутаторы работают не синхронно. Способы уменьшения помех: увеличение периода следования импульсов Т, совершенствование системы синхронизации, увеличение полосы частот системы связи.

1   2   3   4   5

---

2. Энтропия

Количество информации, которое заключено в некотором сообщении с вероятностью появления p(i), равно: I=-log₂p(i).Свойства количества информации:

1)чем меньше р, тем больше I.

2)количество информации в достоверном событии с вероятностью появления p=1 равно 0.

3)аддитивное свойство: количество информации, заключенное в совокупности двух независимых сообщений, равно сумме количеств информации, заключенных в каждом сообщении в отдельности.

4)количество информации величина неотрицательная.

Т.к. сообщения принимают различные значения с разными вероятностями, то ввели понятие энтропии (это среднее количество информации приходящееся на одно сообщение):

H=-∑^m_k=1 p_klogp_k, m – основание кода, p_k - вероятность определенного символа).

Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны: Hmax=logm.

Избыточность это степень отличия энтропии от максимального значения: R=(Hmax-H)/Hmax.

Энтропия двоичного источника вычисляется по формуле:

H(m=2)=-p(1)*logp(1)-[1-p(1)]log[1-p(1)]

Энтропия двоичного источника максимальна если p(1)=p(0)=0.5

Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации при заданной бодовой скорости - количество посылок в единицу времени

Основные способы увеличения энтропии:

1)наличие корреляционных связей между символами уменьшает энтропию.

Чтобы увеличить энтропию, мы кодируем не буквы а слова. Это называется укрупнение алфавита источника.

Эта же цель достигается путем предсказания - кодирования с предсказанием последующих символов по предыдущим

2) Неравновероятность символов уменьшает энтропию. Для устранения неравновероятности строят "кодовое дерево". Наиболее вероятные символы передаются наиболее короткими кодовыми комбинациями.

3)Для дальнейшего увеличения энтропии увеличивают основание кода m.


Билет 19

1. ФРК

При ФРК идеально разделены только два канала информации первого канала передается на несущей частоте U1(t)=Umsinw₀t, а второй передается на несущей частоте U2(t)=Umсosw

---

₀t

Разделение каналов осуществляется за счет ортогональных несущих.

При ФРК оба канала передаются одинаково в одной и той же полосе, но разделяются.

Пусто по 1 каналу передается информация U1(t)=Umsinw₀t, а по 2 каналу U2(t)=Umсosw₀t

Прием осуществляется с помощи синхродетектора у которого два входа. На синхронный детектор поступает сумма U1(t)+U2(t), а на второй вход опорное напряжение Uопр(t)=Umsinw₀t , на второй детектор СД2 поступает на первый вход таже суммаU1(t)+U2(t), а на второй вход опорное напряжение Uопр(t)=Umcosw₀t

Напряжение на выходе синхронного детектора равно:

U_выхСД1=∫[ U1(t)+U2(t)] Uопр1(t)dt=1/T∫ U1(t) sinw₀t sinw₀t dt+1/T∫U2(t) cosw₀t sinw₀t dt= 1/T∫(U1(t)Um)/2=(U1(t) за время t практический не миняется)= U1(t)Um)/2 это информация 1-го канала.

Причины взаимных помех: разность фаз несущих частот на передача не равно 90⁰; фазы опорных напряжений не равны точно фазам несущих частот первого и второго каналов; операция интегрирования реализуется с погрешностями. Способы уменьшения взаимных помех: усовершенствовать систему частотной и фазовой синхронизации; следует уменьшить погрешности реализации операции интегрирования.

2. Циклический код (7,4)

Код называется циклическим, если циклическая перестановка одной кодовой комбинации дает все остальные кодовые комбинации данного кода.

10110

01011

10101

11010

Код называется циклическим, если циклическая перестановка одной кодовой комбинации дает все остальные кодовые комбинации данного кода. Каждая комбинация такого кода записывается в виде полинома. Состоит из 7 символов, из которых 4 информационных и 3 проверочных.

Алгоритм формирования: записываются возможные информационные комбинации; каждую комбинацию записывают в виде полинома (а3,а2,а1,а0); выбираем образующий полином, степень которого соответствует количеству проверочных символов ; полином, соответствующий информационной комбинации, умножается на образующий полином.

Алгоритм декодирования: принятая кодовая комбинация делится на образующий полином, остаток от деления есть синдром, который указывает, где произошла ошибка; формируем вектор ошибки (т.е. кодовую комбинацию с ошибкой) на основании синдрома.

Кодовое расстояние – количество позиций, в которых одна кодовая комбинация отличается от другой. Здесь минимальное кодовое расстояние равно 3 (т.е. код исправляет все одиночные ошибки).

---

Теория циклических кодов базируется на теории двоичных полиномов(полиномиальные коды)

Каждая комбинация такого кода записывается в виде полинома


Билет 20

1. Характеристики ЦФ

ЦФ – это микроЭВМ, которая решает задачу фильтрации средствами вычислительной техники. Описывается разностным уравнением, которое является цифровым эквивалентом аналогового дифференциального уравнения: y_i==∑^L_l=1 a_ly_i-l+=∑^M_m=0 b_mx_i-m. Максимум из L,M определяет порядок фильтра.

Характеристики:

Импульсная реакция ЦФ (g) – реакция фильтра на единичный импульс (из разностного уравнения, где для y:реакция не опережает воздействие; для х: 1при i=0, 0 при i≠0).

Переходная характеристика ЦФ (h) – реакция фильтра на дискретную функцию единичного скачка (из разностного уравнения, где для для y:реакция не опережает воздействие; для х: 1при i≥0, 0 при i<0; из импульсной характеристики: h=∑ⁱ_k=0 g_k).

Передаточная характеристика ЦФ (K(z)) – отношение z-преобразования выходного процесса y(z) к z-преобразованию входного процесса x(z). Из нее можно получить выражения для АЧХ и ФЧХ фильтра, а также определить является ли фильтр устойчивым (корни числителя – нули, корни знаменателя – полюсы; ЦФ устойчив если полюсы лежат внутри окружности единичного радиуса).
2. Оптимальный корреляционный приемник

Оптимальный корреляционный приемник - это приемник для двоичных сигналов с одинаковой энергией

Приемник реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником

Эта минимальная вероятность ошибки может быть большой, но никакой другой приемник не даст меньшей вероятности ошибки.

Правило работы оптимального приемника может быть только статистическим.

∫U₁²(t)dt=∫U₀²(t)dt (c одинаковыми энергиями)

Алгоритм работы:

∫[z²(t)-2z(t)U₁(t)+ U₁²(t)]dt <∫[z²(t)-z(t)U₀(t)+ U₀²(t)]dt то R=1;

И тогда

∫z(t)U₁(t)dt > ∫z(t)U₀(t)dt то R=1

∫z(t)U₁(t)dt < ∫z(t)U₀(t)dt то R=0
Структурная схема:


Генер U1(t)


1




Перемн

---

Интегр.



РУ

Z(t)










Перемн

Интегр.

2










Генер U0(t)

Билет 21

1. СФ

Оптимальный фильтр – это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется согласованным фильтром.

Фильтр называется согласованным т.к.:

1)обеспечивает максимальное отношение с/ш на выходе: h0²=Ec/G0

2)характеристики СФ согласованы с характеристиками сигнала

а)импульсная реакция СФ совпадает с зеркальным отображением согласованного с ним сигнала

б) АЧХ СФ совпадает с амплитудным спектром сигнала(с точностью до постоянного множителя)

в)ФЧХ СФ противоположна по знаку ФЧХ сигнала

Докажем основные свойства согласованного фильтра:

Uвых(t)=∫z(τ)g(t-τ)d τ= ∫Uc(τ)g(t- τ)dτ +∫x(τ)g(t- τ)dτ – напряжение на выходе фильтра.

Напряжение полезного сигнала ∫Uc(τ)g(t- τ)dτ.

Мощность полезного сигнала [∫Uc(τ)gcф(t- τ)dτ]² (на единичном сопротивлении).

Мощность помехи (дисперсия)

[∫x(τ)g(t- τ)dτ]²=∫x(τ)g(t- τ)dτ*∫x(V)g(t- V)dV=G₀∫б(τ-V)g(t-τ)dτ∫ g(t-V)dV=G0∫ g²(t-V)dV

Где В(τ-v)= x(τ)x(V)=G₀ δ (τ-V)

Используем фильтрующие свойства δ-функции

∫ δ (τ-V)y(t)dt=y(τ) то есть ∫ δ (τ-V)g(t-τ)dτ= g(t-V)

Отношение сигнал и шум:

Pc/σ²=[∫Uc(τ)g(t- τ)dτ]²/ G₀∫ g²(t-V)dV≤ ∫U²c(τ)g²(t- τ)dτ / G₀∫ g²(t-V)dV≤ ∫ U²c(τ)dτ/ G₀

Поскольку подынтегральное выражение не отрицательно, то интеграл будет максимален. Согласованный фильтр дает на выходе в момент времени t=T максимальное отношение сигнал шум, равный h0=∫ U

---

Смотрите также файлы

• Эссе по фильму Восхождение к праву студентки группы лпп 1412 Плаховой Дарьи.docx

• Задание Опишите правила согласования географических названий. Задание 2.docx

• Чн20Э271 Студент Е. И. Башилова москва 2022 Вопросы Укажите основные этапы эконометрического исследования.docx

• Лабораторная работа 1 по учебному курсу Экология.docx

• Задача Сформируйте инвестиционный портфель предприятия, если предприятие располагает суммой 800 д е., ожидаемая норма доходности 15%.docx