Вопросы к экзамену по математическому анализу (1 семестр)
Определение предела последовательности. Предельные точки множества членов последовательности. Подпоследовательность, частичный предел.

Принцип вложенных отрезков. Теорема Больцано-Вейерштрасса.

Фундаментальная последовательность. Критерий сходимости Коши.

Свойства сходящихся последовательностей

Определение предела функции в точке. Свойства функций, имеющих предел (арифметические действия с пределами, о пределе суперпозиции, о пределе промежуточной функции).

Непрерывность функции в точке. Теоремы о непрерывности арифметических действий, о непрерывности сложной функции.

Точки разрыва функции и их классификация.

Бесконечно малые и бесконечно большие функции. Теорема о связи бесконечно малых и бесконечно больших функций.

Свойства бесконечно малых функций. Арифметические действия, теорема о произведении бесконечно малой функции на ограниченную.

Сравнение роста и убывания функций. Символы о-малое и о-большое.

Теоремы о первом и втором замечательном пределах.

Таблица эквивалентностей. Раскрытие неопределенностей.

Теорема о замене бесконечно малых функций эквивалентными при вычислении предела отношения функций.

Производная, ее геометрический и механический смысл. Правила дифференцирования.

Дифференциал функции, его геометрический смысл. Необходимое и достаточное условие дифференцируемости

Связь непрерывности и дифференцируемости.

Производная сложной и обратной функции.

Теорема Ролля, ее геометрический смысл.

Теорема Лагранжа, ее геометрический смысл. Теорема Коши.

Правило Лопиталя

Основные тейлоровские разложения.

Теорема единственности представления функции в виде многочлена Тейлора.

Локальный экстремум функции одного переменного. Необходимое условие экстремума

Достаточные условия локального экстремума (по первой и второй производной)

Точки перегиба. Необходимое и достаточное условие перегиба.

Необходимые и достаточные условия монотонности и выпуклости функции.

Вертикальные и наклонные асимптоты графика функции.

---

Примеры вопросов при тестировании
1.Предел числовой последовательности. Существование предела монотонной ограниченной последовательности. Единственность предела последовательности.
2.Определение предела функции в точке. Дать геометрическую иллюстрацию

и сформулировать с помощью логической символики утверждение

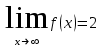
3.Предел функции в точке. Свойства пределов. Раскрытие

неопределенностей ∞/∞ и 0/0

Вычислить предел
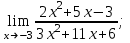
4. Первый замечательный предел.
6. Второй замечательный предел. Раскрытие неопределённостей

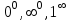
Вычислить ..

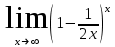7. Бесконечно большие функции. Теорема о связи бесконечно малых и бесконечно больших функций

Привести примеры бесконечно больших функций.

8. Сравнение бесконечно малых. Эквивалентность бесконечно малых. Основные

эквивалентности

9. Теорема о замене бесконечно малых функций эквивалентными при вычислении пределов.
Примеры.

10. Определение непрерывности функции в точке и на отрезке. Примеры.

Свойства функций, непрерывных на отрезке.

Исследовать функцию 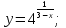на непрерывность

11. Определение непрерывности функции в точке и на отрезке. Точки разрыва, их классификация.
Исследовать функцию 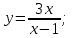на непрерывность.

12. Определение непрерывности функции в точке и на отрезке. Точки разрыва, их классификация
Исследовать функцию 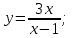на непрерывность.

13.Определение дифференцируемости функции одной переменной в точке.

Определение дифференциала функции, его геометрический смысл.


14.Доказать теорему о связи дифференцируемости и непрерывности функции

в точке

Привести пример непрерывной, но не дифференцируемой функции.

15.Определение производной. Арифметические свойства производных.

Вычислить производную функции
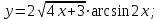
16. Определение производной. Таблица производных. Вывод формул дифференцирования тригонометрических функций.

17. Определение производной. Таблица производных. Вывод формул дифференцирования показательной и логарифмических функций

---

18.Определение производной. Производная сложной функции.

Вычислить производную функции

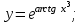
19.Дифференциал сложной функции. Инвариантность дифференциала функции одной переменной.

Найти дифференциал функции

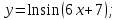
20.Определение производной. Производная обратной функции. Вывод формулы производной обратной тригонометрической функции
21. Определение производной. Производная функции, заданной неявно и параметрически.

Найти производную функции

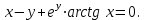
22. Метод логарифмического дифференцирования. Дифференцирование показательно-степенных функций

Найти производную функции

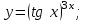
23.Теорема Ролля, её геометрический смысл,
24.Теорема Лагранжа, её геометрический смысл. Формула конечных приращений.
25.Теорема Коши
26. Правило Лопиталя. Доказательство для случая .
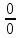27. Сравнение роста показательной, степенной и логарифмической функций при х --∞
28. Условия постоянства, возрастания и убывания функции
Исследовать функцию 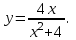на монотонность.

29. Определение экстремума функции. Необходимое условие существования экстремума функции.
Исследовать функцию 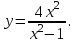на экстремум.

30. Определение экстремума функции. Достаточное условие экстремума по первой производной.

Исследовать функцию 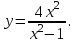на экстремум

31.Выпуклость и вогнутость графика функции. Точки перегиба.

Исследовать функцию 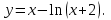на выпуклость и вогнутость

32 Вертикальные асимптоты графика функции.

Есть ли у функции 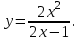вертикальные асимптоты

33. Наклонные асимптоты графика функции. Необходимые и достаточные условия существования наклонной асимптоты

Исследовать функцию 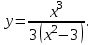на существование наклонных асимптот

34.Общая сема исследования функции и построения графика.

---

35. Полярная система координат. Связь полярных и прямоугольных координат точки.

Записать уравнение линии x²+y²=4x в полярной системе координат

36.График функции в полярной системе координат.

Построить график функции ρ=2cosφ в полярной системе координат.

---

Смотрите также файлы

• Выполнение практических заданий по дисциплине трудовое право.docx

• Д идро Дени (17131784).docx

• Выполнение практических заданий по дисциплине бухгалтерский учет и анализ.docx

• 1. Острая сердечная недостаточность (оссн)острые нарушения ритма, гипертонический криз, внезапная остановка сердца.docx

• Страна Событие.docx