Файл: Самостоятельная работа по теме Задание 1 Постройте произвольные параллелограмм общего вида, квадрат, прямоугольник, ромб.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 24
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2.2 Геометрические фигуры в пространстве
Самостоятельная работа по теме 2.2.
Задание 1.
Найдите объем правильной четырехугольной призмы, сторона которой 5 см, а высота 8 см
Решение
Правильная четырехугольная призма - это четырехугольная призма, у которой основания квадраты, а боковые грани прямоугольники. Данное геометрическое тело по своим свойствам и характеристикам соответствует - параллелепипеду. Основания призмы являются равными квадратами.
Боковые грани призмы являются прямоугольниками. Боковые рёбра призмы параллельны и равны.
V = a•b•c
V = 5•5•8 = 200 (cм3)
Ответ. 200 cм3.
Задание 2.
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение
V= (2•2•2) - (1•1•2) = 6 (ед.3)
Ответ. 6 ед.3.
Задание 3.
В сосуд цилиндрической формы, объем которого 2400 см3, налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.
Решение
Будем считать, что налитая жидкость – вода, плотность которой равна 1г/см3.
Тогда объём вытесненной телом жидкости равен объёму этого тела.
Значит искомый объём будет равен:
1) V = 2400 •2/3= 1600 (см3) – свободный объём после того, как сосуд заполнили на треть.
2) V = 1600 •1/4= 400 (см3)
Ответ. 400 см3.
Задание 4
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые
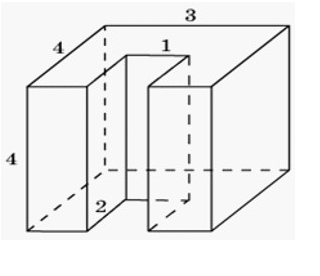
Решение
V= (4•4•3) - (4•1•2) = 40 (ед.3)
Ответ. 40 ед.3.
Практическое задание
Практическое занятие 1.
Задание 4
Внимательно изучите распределение пассажиров (в млн. чел) по видам транспорта. Определите соответствие исходных данных в графическом выражении в виде диаграммы.
Для выбора ответа наведите курсор на верную диаграмму и кликните левой кнопкой компьютерной мыши.
Решение
Ответ. 2.
Практическое занятие 1.
Задание 8
Рассмотрите примеры решений и найдите среди них верные, обозначив их
, и неверные, с обозначением 
, для этого расположите примеры решений в соответствующих областях, путем перемещения примера к левостороннему или правостороннему полю.
Решение.
Практическое занятие 1.
Задание 9
Рассмотрите десятичные дроби и определите, какие из них относятся к периодическим и непериодическим. Переместите дроби в левостороннее или правостороннее поле, кликнув левой кнопкой компьютерной мыши.
Решение.
Практическое занятие 1.
Задание 12
Рассмотрите графические условия. Найдите величину при каждом заданном графическом условии и впишите правильный ответ в виде числового значения.
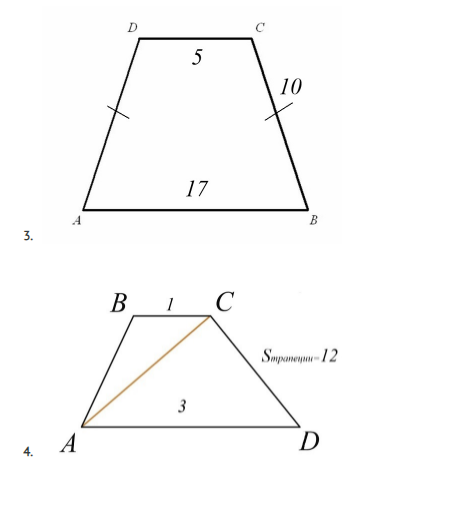
Впишите цифры
1. Площадь треугольника составила 48 кв.ед.
2. Площадь треугольника составила 25 кв.ед.
3. Площадь трапеции составила 88 кв.ед.
4. Площадь треугольника АВС составила 3 кв.ед.
Практическое занятие 2
Задание 1. (Максимальное количество баллов – 3 балла)
Таблица – «Виды моделирования при решении текстовых задач»
В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
Задание 2. (Максимальное количество баллов – 3 балла)
Используя диаграммы Эйлера-Венна решить задачу.
При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей – пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:
1) не желают водить детей в кружки;
2) выбрали не менее двух кружков.
Р
ешение
Рис.=60% Гим.=50%
30%
10%
40% 20%
Муз.=50%
1) Сосчитаем проценты каждой части множеств, тогда получим:
Рис.=60% Гим.=50%
нет 20% 10%
10%
30% 10%
нет
Муз.=50%
Зел – один кружок, Син – два кружка, Крас – три кружка.
2) Составим выражение, процентное соотношение родителей, которые
не желают водить детей в кружки:
100% - (20+10+30+10+10) = 20%
3) Составим выражение, процентное соотношение родителей, которые выбрали не менее двух кружков, т.е. два или три:
20+10+30+10 = 70%
Ответ. 1) 20% не желают водить детей в кружки;
2) 70% выбрали не менее двух кружков.
Задание 3 (максимальное количество баллов – 5 баллов)
При измерении получены данные:
Выполните задания с учетом исходных данных, подробно описывая ход решения.
a) Построить статистический ряд распределения частот.
b) Построить полигон распределения.
c) Вычислить выборочную среднюю, дисперсию, моду, медиану.
d) Построить выборочную функцию распределения.
Решение
a) Построить статистический ряд распределения частот.
Подсчитаем объем, выборка из генеральной совокупности: n=10.
Подсчитаем количество данных:
«5» – 3
«10» – 2
«15» – 1
«20» – 4
Всего:10
Получили ряд: 3, 2, 1, 4
Запишем в таблицу:
Построенный вариационный ряд также называют статистическим распределением выборки.
b) Построить полигон распределения.
Д
ля построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками
4
………………………………………………….
3
…………………………………………….
2
……………………………………………….
1
……………………………………………………….
0 5 10 15 20
c) Вычислить выборочную среднюю, дисперсию, моду, медиану.
1) Найдём выборочную среднюю:
(5•3+10•2+15+20•4) : 10 = 13
Или так:
(20+20+5+10+10+15+20+5+5+20) : 10 = 13.
2) Найдём дисперсию:
Для этого Сумму всех xi надо разделить на n^
(5+10+15+20):4 = 12,5
3) Найдём моду:
Мода М0 дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае М
Самостоятельная работа по теме 2.2.
Задание 1.
Найдите объем правильной четырехугольной призмы, сторона которой 5 см, а высота 8 см
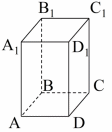 | Дано: ABCDA1B1C1D1 – призма, ABCD = A1B1C1D1 – квадраты, AD = 5 cм, H = 8 cм. Найти: V. |
Решение
Правильная четырехугольная призма - это четырехугольная призма, у которой основания квадраты, а боковые грани прямоугольники. Данное геометрическое тело по своим свойствам и характеристикам соответствует - параллелепипеду. Основания призмы являются равными квадратами.
Боковые грани призмы являются прямоугольниками. Боковые рёбра призмы параллельны и равны.
V = a•b•c
V = 5•5•8 = 200 (cм3)
Ответ. 200 cм3.
Задание 2.
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение
V= (2•2•2) - (1•1•2) = 6 (ед.3)
Ответ. 6 ед.3.
Задание 3.
В сосуд цилиндрической формы, объем которого 2400 см3, налили жидкость, заполнив сосуд на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических сантиметрах.
Решение
Будем считать, что налитая жидкость – вода, плотность которой равна 1г/см3.
Тогда объём вытесненной телом жидкости равен объёму этого тела.
Значит искомый объём будет равен:
1) V = 2400 •2/3= 1600 (см3) – свободный объём после того, как сосуд заполнили на треть.
2) V = 1600 •1/4= 400 (см3)
Ответ. 400 см3.
Задание 4
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые
Решение
V= (4•4•3) - (4•1•2) = 40 (ед.3)
Ответ. 40 ед.3.
Практическое задание
Практическое занятие 1.
Задание 4
Внимательно изучите распределение пассажиров (в млн. чел) по видам транспорта. Определите соответствие исходных данных в графическом выражении в виде диаграммы.
Для выбора ответа наведите курсор на верную диаграмму и кликните левой кнопкой компьютерной мыши.
Решение
Ответ. 2.
Практическое занятие 1.
Задание 8
Рассмотрите примеры решений и найдите среди них верные, обозначив их
, и неверные, с обозначением , для этого расположите примеры решений в соответствующих областях, путем перемещения примера к левостороннему или правостороннему полю. Решение.
   |  |   |
Практическое занятие 1.
Задание 9
Рассмотрите десятичные дроби и определите, какие из них относятся к периодическим и непериодическим. Переместите дроби в левостороннее или правостороннее поле, кликнув левой кнопкой компьютерной мыши.
Решение.
   |  |     |
Практическое занятие 1.
Задание 12
Рассмотрите графические условия. Найдите величину при каждом заданном графическом условии и впишите правильный ответ в виде числового значения.
Впишите цифры
1. Площадь треугольника составила 48 кв.ед.
2. Площадь треугольника составила 25 кв.ед.
3. Площадь трапеции составила 88 кв.ед.
4. Площадь треугольника АВС составила 3 кв.ед.
Практическое занятие 2
Задание 1. (Максимальное количество баллов – 3 балла)
Таблица – «Виды моделирования при решении текстовых задач»
В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
| Задача | Модель | Интерпретация модели |
| 1  . 1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось? |     | Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта. Необходимо определить числовое значение величины конечного состояния объекта. |
| 2. Было 4 кубика, стало 7 кубиков. Что произошло? |   74 | Известно: начальное и конечное состояние объекта; направленность отношения между ними. Необходимо определить: направленность отношения между начальным и конечным состоянием объекта |
| 3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления? |  7? 4 | Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определить числовое значение величины начального состояния объекта. |
| 4.Было 7 кубиков, стало 4 кубика. Что произошло? |  | Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта. Необходимо определить числовое значение величины отношения между состояниями объекта.... |
| 5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате? |  | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Необходимо определить . числовое значение величины отношения между состояниями объекта.. |
| 6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате? | 7 4 | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить числовое значение величины отношения между состояниями объекта... |
| 7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз? | | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. Необходимо определить числовое значение величины отношения между состояниями объекта... .... |
| 8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз? | | Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта. Необходимо определить числовое значение величины отношения между состояниями объекта ... |
Задание 2. (Максимальное количество баллов – 3 балла)
Используя диаграммы Эйлера-Венна решить задачу.
При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей – пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:
1) не желают водить детей в кружки;
2) выбрали не менее двух кружков.
Р
ешениеРис.=60% Гим.=50%
30%10%
40% 20%
Муз.=50%
1) Сосчитаем проценты каждой части множеств, тогда получим:
Рис.=60% Гим.=50%
нет 20% 10%10%
30% 10%
нет
Муз.=50%
Зел – один кружок, Син – два кружка, Крас – три кружка.
2) Составим выражение, процентное соотношение родителей, которые
не желают водить детей в кружки:
100% - (20+10+30+10+10) = 20%
3) Составим выражение, процентное соотношение родителей, которые выбрали не менее двух кружков, т.е. два или три:
20+10+30+10 = 70%
Ответ. 1) 20% не желают водить детей в кружки;
2) 70% выбрали не менее двух кружков.
Задание 3 (максимальное количество баллов – 5 баллов)
При измерении получены данные:
| Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Данные | 20 | 20 | 5 | 10 | 10 | 15 | 20 | 5 | 5 | 20 |
Выполните задания с учетом исходных данных, подробно описывая ход решения.
a) Построить статистический ряд распределения частот.
b) Построить полигон распределения.
c) Вычислить выборочную среднюю, дисперсию, моду, медиану.
d) Построить выборочную функцию распределения.
Решение
a) Построить статистический ряд распределения частот.
Подсчитаем объем, выборка из генеральной совокупности: n=10.
Подсчитаем количество данных:
«5» – 3
«10» – 2
«15» – 1
«20» – 4
Всего:10
Получили ряд: 3, 2, 1, 4
Запишем в таблицу:
| xi | ni |
| 5 | 3 |
| 10 | 2 |
| 15 | 1 |
| 20 | 4 |
| ∑ | 10 |
Построенный вариационный ряд также называют статистическим распределением выборки.
b) Построить полигон распределения.
Д
ля построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты и полученные точки соединим отрезками4
………………………………………………….3
…………………………………………….2
……………………………………………….1
………………………………………………………. 0 5 10 15 20
c) Вычислить выборочную среднюю, дисперсию, моду, медиану.
1) Найдём выборочную среднюю:
(5•3+10•2+15+20•4) : 10 = 13
Или так:
(20+20+5+10+10+15+20+5+5+20) : 10 = 13.
2) Найдём дисперсию:
Для этого Сумму всех xi надо разделить на n^
(5+10+15+20):4 = 12,5
3) Найдём моду:
Мода М0 дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае М