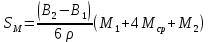МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

Сибирский Государственный Университет Геосистем и Технологий

(ФГБОУ ВО СГУГиТ)

Институт геодезии и менеджмента

Кафедра высшей геодезии

Лабораторная работа № 1

Вычисление радиусов кривизны сечений различных эллипсоидов

Выполнила ст.гр. МД-41

Тарначы А. Н.

Проверил:

Малков А.Г.

Новосибирск, 2016

Цель работы: Усвоить закономерности, связанные с кривизной поверхности эллипсоида.

Содержание:

1. 
   Для пункта с заданными широтами вычислить (для референц-эллипсоида Красовского и общеземного эллипсоида):
   

• 
  радиусы кривизны главных нормальных сечений;
  
• 
  радиусы кривизны по различным направлениям с интервалом по азимуту 30 ̊;
  
• 
  средний радиус кривизны.
  

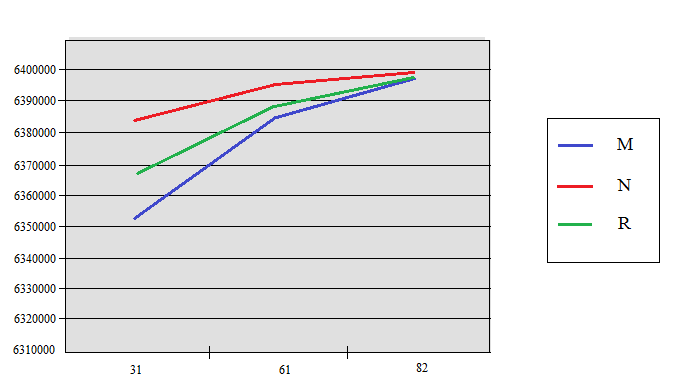
По этим данным построить графики изменения радиуса кривизны.

2. 
   Для этого же пункта вычислить радиус параллели и длины дуг параллелей и меридианов равным 3 градусам.
   

Литература:

1. 
   Хаимов З.С. Основы высшей геодезии . М:Недра, 1984.
   
2. 
   Яковлев Н.В. Практикум по высшей геодезии. М:Недра, 1982.
   

Контрольные вопросы:

1. 
   Какие сечения эллипсоида называют нормальными?
   
2. 
   В чем особенность главных нормальных сечений?
   
3. 
   Какие сечения являются главными нормальными сечениями для поверхности эллипсоида?
   
4. 
   Как изменяется радиус кривизны в зависимости от направления?
   
5. 
   Дайте определение среднего радиуса кривизны?
   
6. 
   Является ли параллель нормальным сечением?
   

Ход работы :

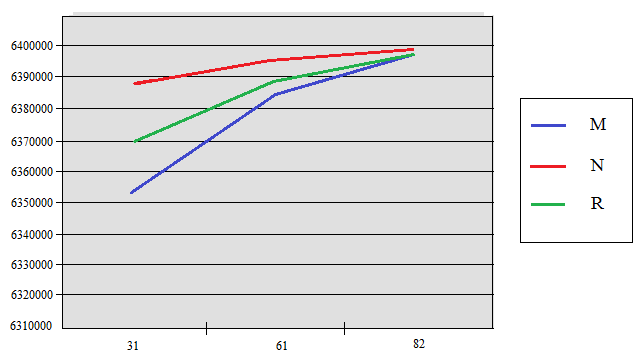
Используемые формулы:

1. 
   – радиус кривизны меридиана
   

---

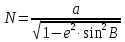
– радиус кривизны первого вертикала

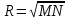– средний радиус кривизны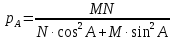

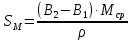2. 
   
   

- длины дуг меридианов 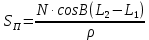– длины дуг параллелей

Референц-эллипсоид Красовского:

a=6378245

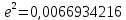
B	M(м)	N(м)	R(м)	ƍ(м)
31°	6352463	6383914	6368169	6360775
61°	6384524	6394636	6389577	6392256
82°	6398446	6399281	6398863	6399264

Общеземной эллипсоид:

а=6378136

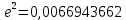
B	M(м)	N(м)	R(м)	ƍ(м)
31°	6352351	6389482	6370889	6362158
61°	6384416	6394529	6389470	6392149
82°	6398339	6399174	6398756	6399157

Референц-эллипсоид Красовского:

a=6378245

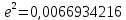
B	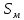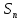(м)	(м)
31°	332478	286517
61°	334365	162324
82°	335042	46632

---

Общеземной эллипсоид:

а=6378136

B	(м)	(м)
31°	332686	286767
61°	334360	162322
82°	335037	46631

Вывод: В данной работе для пункта с широтами 31°, 61°, 82°, для референц-эллипсоида Крассовского и общеземного эллипсоида вычислили радиусы кривизны главных нормальных сечений, радиусы кривизны по различным направлениям с интервалом по азимуту 30°, средний радиус кривизны.

Для этого же пункта вычислили радиус параллели и длины дуг параллелей и меридианов равным 3°.

---

Смотрите также файлы

• Профилактика, устранение негативного фактора.doc

• Учебная программа по дисциплине (с учебнометодической картой дисциплины). Пояснительная записка электронный учебнометодический комплекс Краеведение Беларуси.doc

• Вопросы к промежуточной аттестации по дисциплине.docx

• Процесс снабжения. Логистический процесс государственных закупок.docx

• Распродажи, торговые скидки идругие маркетинговые приемы торговых сетей это обман или благо для потребителя.docx