Автономная некоммерческая организация профессионального образования

«Открытый социально – экономический колледж»

Информатика
Практическое занятие №2

Выполнил:

слушатель Могиленко Сергей Вадимович

Преподаватель:

Каргина Ольга Ивановна
Г. Ростов-на-Дону

Практическое занятие 2.

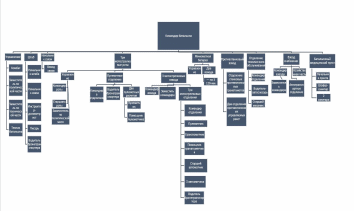
1.      Изобразить в виде графа информацию об организации мотострелковых (мотопехотных) батальонов армии СССР:

«В середине 70-х гг. мотострелковый батальон Советской Армии насчитывал 395 человек и имел следующую структуру. Во главе стоял командир батальона. Ему подчинялись управление, штаб, 3 мотострелковые роты, взвод связи, минометная батарея, противотанковый взвод, отделение технического обслуживания, взвод снабжения и батальонный медицинский пункт. В управление батальоном входили сам комбат, заместитель по политической части, заместитель по технической части и техник батальона. Штаб состоял из начальника штаба, начальника связи, инструктора-дозиметриста, писаря и водителя бронетранспортера. Начальник связи являлся командиром взвода связи (еще 12 чел.). Минометная батарея состояла из управления (10 чел.) и двух взводов по 20 чел., в каждом — по 3 120-мм миномета. Противотанковый взвод состоял из отделения станковых противотанковых гранатометов (8 чел., 2 гранатомета СПГ-9) и двух отделений противотанковых управляемых ракет (по 6 чел. и по 2 ПТУРС в отделении). Отделение технического обслуживания: командир отделения, водитель-автослесарь и старший механик. Взвод снабжения: командир взвода, его заместитель, хозяйственная часть (3 чел.) и автотранспортное отделение (4 чел.). Батальонный медицинский пункт: начальник пункта, шофер-санитар и 2 санитара. Мотострелковая рота состояла из управления (командир роты, заместитель по политической части, старшина роты), пулеметного отделения и 3 мотострелковых взводов. Пулеметное отделение состояло из командира отделения, водителя бронетранспортера и двух пулеметных расчетов, в каждом пулеметчик и помощник пулеметчика. Мотострелковый взвод имел командира взвода, заместителя командира и 3 мотострелковых отделения. В каждом отделении: командир отделения, пулеметчик, гранатометчик, помощник гранатометчика, старший автоматчик, 3 автоматчика и водитель бронетранспортера.»

---

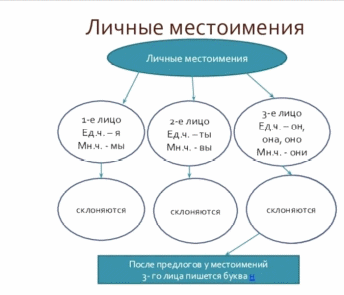
2.      Представить информацию о классификации в русском языке в виде графа. Является ли полученный граф деревом?

Местоимения в русском языке бывают трех лиц: 1-го, 2-го и 3-го. Во всех трех лицах они могут быть единственного и множественного числа. Местоимения 3-го лица единственного числа кроме того изменяются по родам. Местоимение 1-го лица единственного числа — я, местоимение 1-го лица множественного числа — мы. Местоимение 2-го лица единственного числа — ты, местоимение 2-го лица множественного числа — вы. Местоимения 3-го лица единственного числа: мужского рода — он, женского рода — она, среднего рода — оно. Местоимение 3-го лица множественного числа — они.

3.      На основании исходных данных постройте аддитивную модель временного ряда

 

Месяц	Удельный вес частного жилья в объеме строительства %
Сентябрь	37,5
Октябрь	27,5
Ноябрь	23,5
Декабрь	41,0
Январь	43,3
Февраль	37,2
Март	33,4
Апрель	29,6
Май	31,1

 

Решение

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени.

Аддитивная модель – модель вида: Y=T+S+E,

где Т - трендовая компонента;

S – циклическая компонента;

---

Е – случайная компонента.

Алгоритм построения аддитивной модели.

Шаг1. Выравнивание исходных уровней ряда методом скользящей средней:

            1. Суммируем уровни ряда последовательно за каждый промежуток времени, в котором наблюдаются колебания со сдвигом на один момент времени и определяем условные величины показателя Y.

            2. Делим полученные величины на число моментов времени в промежутке и находим скользящие средние.

            3. Находим средние значения из двух последовательных скользящих средних – центрированные скользящие средние.

Шаг 2. Оценка сезонной компоненты:

            1. Находим оценку сезонной компоненты, как разность между фактическими уровнями ряда и центрированными скользящими средними.

            2. Находим средние оценки сезонной компоненты за каждый промежуток времени, в котором наблюдаются колебания 
.

            3. Исходя из условия взаимопогашения сезонных воздействий определяем корректирующий коэффициент k: в аддитивной модели

; где n – период колебаний.



            4. Рассчитываем скорректированные значения сезонных компонент: в аддитивной модели: 
Шаг 3. Элиминирование влияния сезонной компоненты:

Находим значения Т+Е как Y-S – в аддитивной модели.

Шаг 4. Определение трендовой компоненты ряда.

            1. Трендовая компонента ряда определяется с помощью построения регрессионной модели, параметры которой находятся методом наименьших квадратов.

            2. С помощью уравнения регрессии находим уровни трендовой компоненты Т для каждого момента времени t.

Шаг 6. Находим значения Т+S.

Шаг 7. Находим случайную компоненту Е= Y-(T+S)

Шаг 8. Оценка качества модели.

            1. Находим сумму квадратов случайной компоненты.

            2. Находим отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения: %

---

Ответ:

1.

 

2.

3.

Общий вид аддитивной модели следующий: Y = T + S + E Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (T), сезонной (S) и случайной (E) компонент. Рассчитаем компоненты аддитивной модели временного ряда. На основании исходных данных постройте аддитивную модель временного ряда Месяц Удельный вес частного жилья в объеме строительства % Сентябрь 37,5 Октябрь 27,5 Ноябрь 23,5 Декабрь 41,0 Январь 43,3 Февраль 37,2 Март 33,4 Апрель 29,6 Май 31,1 Месяц Удельный вес частного жилья в объеме строительства % Скользящая средняя Центрированная скользящая средняя Оценка сезонной компоненты Сентябрь 37,5 Октябрь 27,5 Ноябрь 23,5 Декабрь 41,0 Январь 43,3 Февраль 37,2 Март 33,4 Апрель 29,6 Май 31,1 СРЕДНЕЕ РЕШЕНИЕ Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Аддитивная модель – модель вида: Y=T+S+E, где Т - трендовая компонента; S – циклическая компонента; Е – случайная компонента. Алгоритм построения аддитивной модели. Шаг 1. Выравнивание исходных уровней ряда методом скользящей средней: 1. Суммируем уровни ряда последовательно за каждый промежуток времени, в котором наблюдаются колебания со сдвигом на один момент времени и определяем условные величины показателя Y. 2. Делим полученные величины на число моментов времени в промежутке и находим скользящие средние. 3. Находим средние значения из двух последовательных скользящих средних – центрированные скользящие средние. Шаг 2. Оценка сезонной компоненты: 1. Находим оценку сезонной компоненты, как разность между фактическими уровнями ряда и центрированными скользящими средними. 2. Находим средние оценки сезонной компоненты за каждый промежуток времени, в котором наблюдаются колебания. 3. Исходя из условия взаимопогашения сезонных воздействий определяем корректирующий коэффициент k: в аддитивной модели ; где n – период колебаний. 4. Рассчитываем скорректированные значения сезонных компонент: в аддитивной модели: Шаг 3. Элиминирование влияния сезонной компоненты: Находим значения Т+Е как Y-S – в аддитивной модели. Шаг 4. Определение трендовой компоненты ряда. 1. Трендовая компонента ряда определяется с построения регрессионной модели, параметры которой находятся методом наименьших квадратов. 2. С уравнения регрессии находим уровни трендовой компоненты Т для каждого момента времени t. Шаг 6. Находим значения Т+S. Шаг 7. Находим случайную компоненту Е= Y-(T+S) Шаг 8. Оценка качества модели. 1. Находим сумму квадратов случайной компоненты. 2. Находим отношение суммы квадратов случайной компоненты к общей сумме квадратов отклонений уровней ряда от его среднего значения: % ПРИМЕР ВЫПОЛНЕНИЯ ШАГ1. Выравнивание исходных уровней ряда методом скользящей средней: Расчеты отобразим в таблице 1. Таблица 1. Выравнивание исходных уровней ряда t Итого за 3 месяца. скользящая средняя центрированная скользящая средняя Оценка сезонной компоненты 1 36,40 - - - - 2 28,60 87,40 29,13 - - 3 22,40 93,30 31,10 30,12 -7,72 4 42,30 106,30 35,43 33,27 9,03 5 41,60 123,10 41,03 38,23 3,37 6 39,20 113,20 37,73 39,38 -0,18 7 32,40 102,40 34,13 35,93 -3,53 8 30,80 92,80 30,93 32,53 -1,73 9 29,60 60,40 - - - Итого 303,3 778,9 239,48 209,46 -0,76 Выбираем метод сглаживания скользящей средней по трем соседним компонентам ряда. Скользящая средняя. Остальные столбцы вычисляем согласно описанию Месяц Удельный вес частного жилья в объеме строительства % Скользящая средняя Центрированная скользящая средняя Оценка сезонной компоненты Сентябрь 37,5 Октябрь 27,5 Ноябрь 23,5 Декабрь 41,0 Январь 43,3 Февраль 37,2 Март 33,4 Апрель 29,6 Май 31,1 СРЕДНЕЕ

---

---

Смотрите также файлы

• Задача создания документа создать рабочий процесс, при котором франшиза будет расти в показателях и выполнять план.docx

• 1. Конституционные права, свободы и обязанности человека и гражданина.docx

• С точки зрения Л. Фейербаха, источником религии является ограниченность человека.docx

• 1. Выберите два примера нерационального природопользования. 1 проведение снегозадержания в зимнее время.pdf

• Москвина Т. А.(Пгуас фаут зик12).docx