Файл: Решение для минимума Поскольку функция цели F(x) параллельна de то на прямой de функция F(x) будет принимает одно и тоже минимальное значение. Для определения координат точки e решим систему уравнений.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 05.05.2024

Просмотров: 24

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задача 1



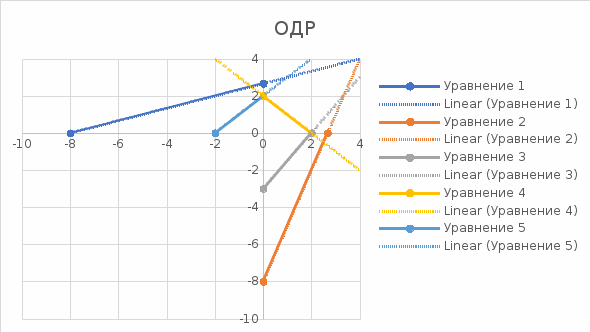
Найдем вначале область допустимых решений (ОДР)

x1-3x2=-8, Эта прямая проходит через точки: (-8,0), ( 0, 8/3).

3x1-x2=8, Эта прямая проходит через точки: (8/3,0), ( 0, -8).

x1-x2=2, Эта прямая проходит через точки: (2,0), ( 0, -2).

x1+x2=2, Эта прямая проходит через точки: (2,0), ( 0, 2).

x1-x2=-2, Эта прямая проходит через точки: (-2,0), ( 0, 2).

x1 ≥ 0,

x2 ≥ 0,
Тривиальным неравенствам x1  0, x2  0 соответствует первая четверть координатной плоскости. Пересечение всех указанных полуплоскостей определяет ОДР данной задачи.





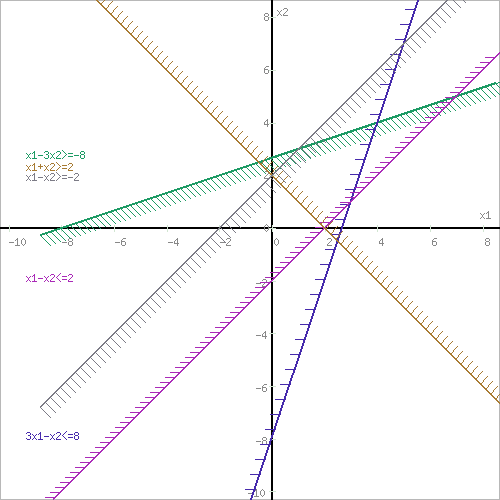
Выделив область решения каждого неравенства системы ограничений, получим многоугольник допустимых решений нашей задачи.



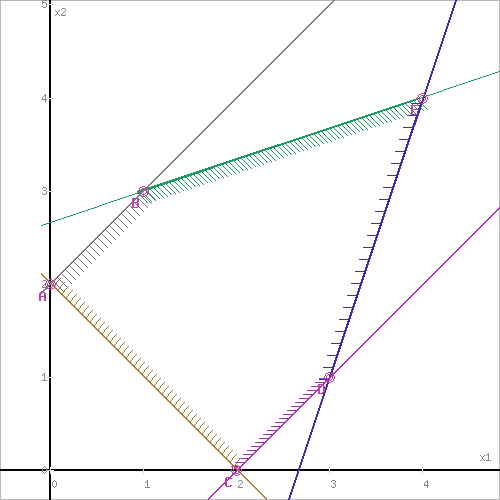
Получили многоугольник ABCDE

Построим основную прямую F = -9x1+3x2+18 = 0, проходящую через начало координат O(0,0) перпендикулярно вектору c(-9;3).



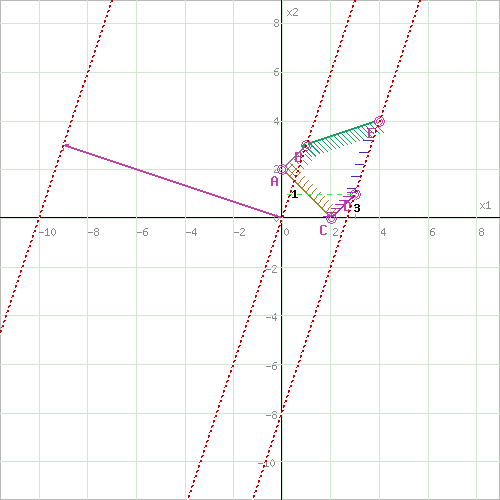
Перемещая прямую F в направлении вектора c(-9;3), находим минимальную точку D, в которой пересекаются прямые 2 и L:

3x1-x2=8

x1-x2=2

Решим систему уравнений и получим: x1 = 3, x2 = 1

Откуда найдем минимальное значение целевой функции:

F(x) = -9∙3 + 3∙1 + 18 = -6

Решение для минимума:



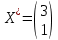
Поскольку функция цели F(x) параллельна DE то на прямой DE функция F(x) будет принимает одно и тоже минимальное значение.
Для определения координат точки E решим систему уравнений:
x1-3x2=-8
3x1-x2=8
Получим: x1 = 4, x2 = 4

F(x) = -9∙4 + 3∙4 + 18 = -6 тоже самое минимальное значение.

Решение для минимума:



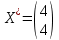
Перемещая прямую F в направлении вектора c(-9;3), находим максимальную точку A, в которой пересекаются прямые 5 и 6:

x1-x2=-2

x1=0

Решив систему уравнений, получим: x1 = 0, x2 = 2

Откуда найдем максимальное значение целевой функции:

F(x) = -9∙0 + 3∙2 + 18 = 24

Решение для максимума:



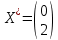
Ответ: Минимальное значение -6 достигается при x1 = 3, x2 = 1. Максимальное значение 24 достигается при x1 = 0, x2 = 2.
Задача 2


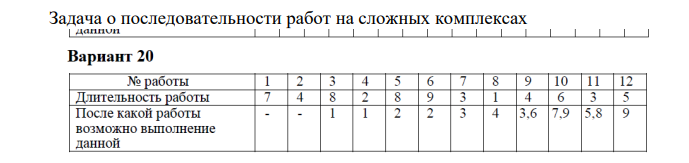
Строим граф:



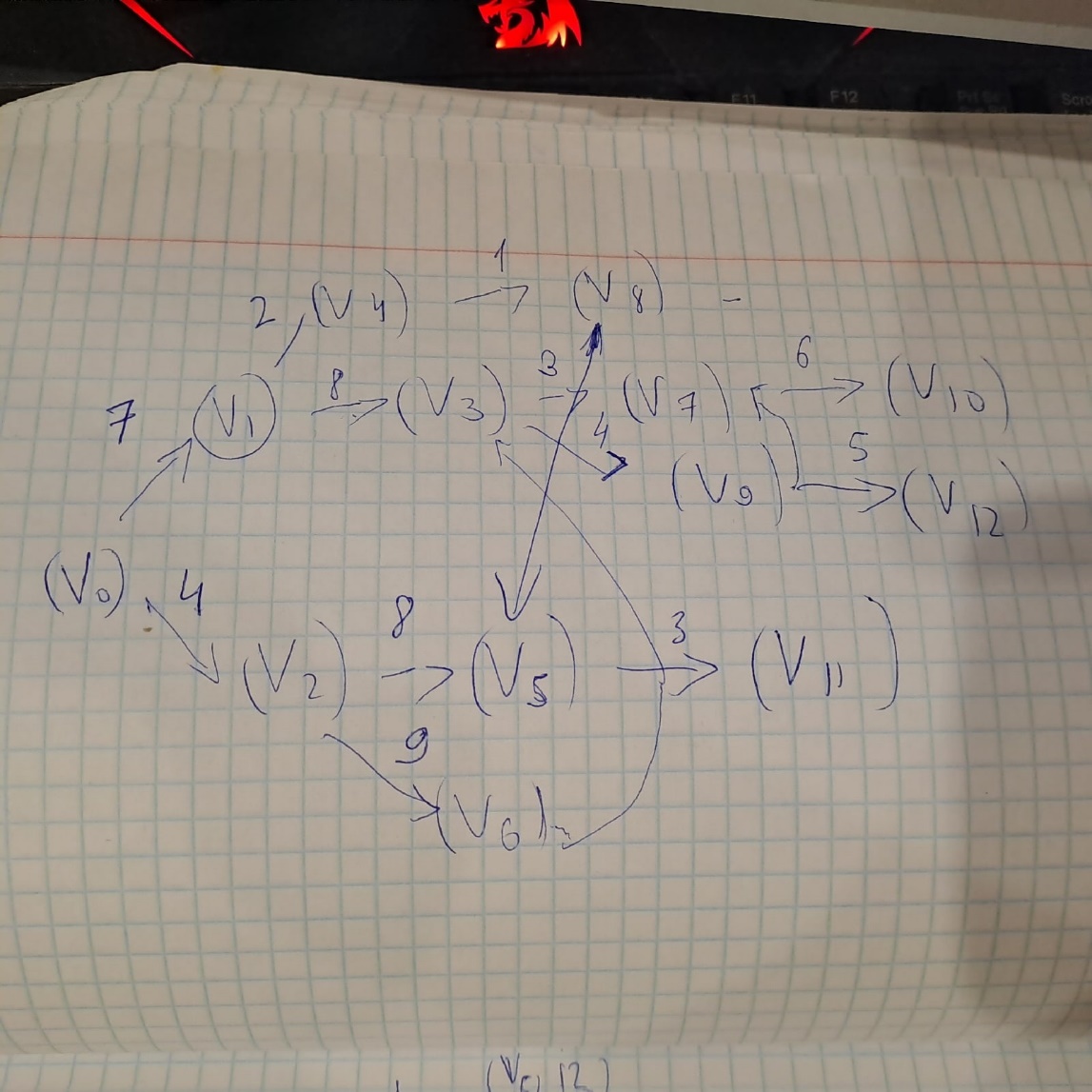
Каждой вершине присвоим двойную метку Vi ,li , где Vi – вершина из которой путь приходит, li – длина пути до этой вершины.

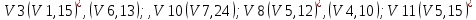
Отметим красным цветом наилучший путь и запишем его.





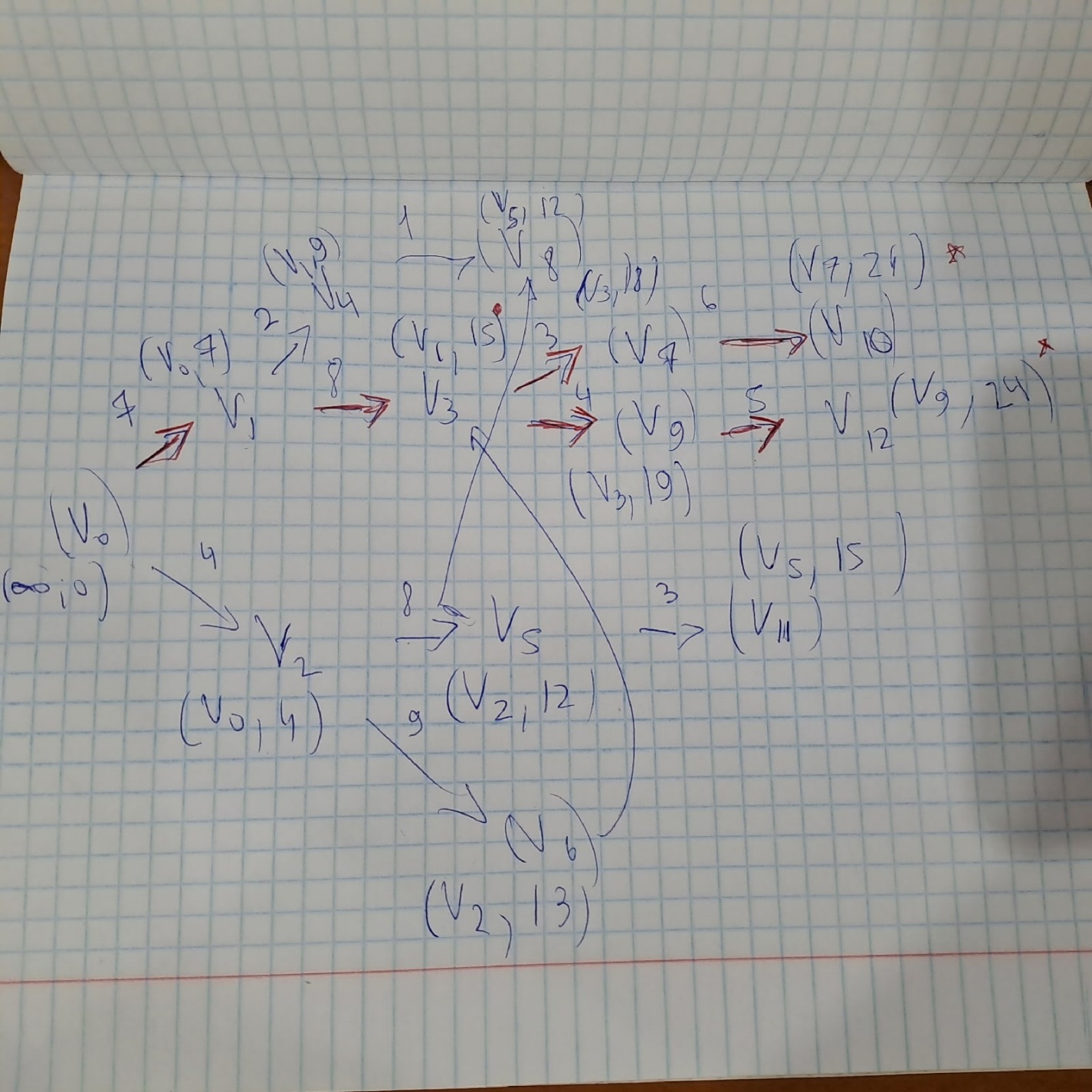
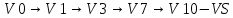
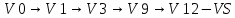
Lmax = 24

Ответ: Lmax = 24,




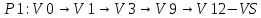
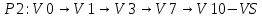
Задача 3


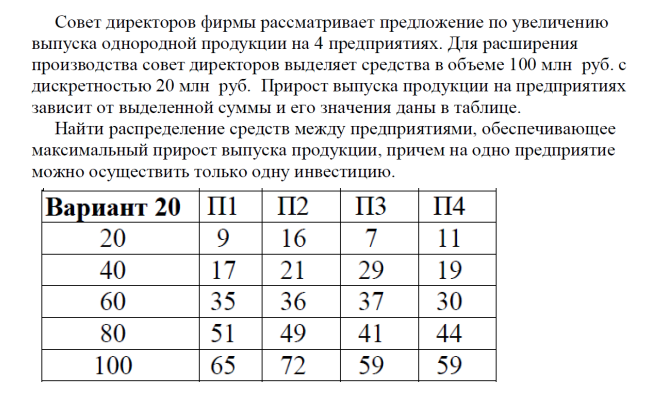
Исходные данные.

f1
f2
f3
f4
xi

0
0
0
0
0

9
16
7
11
20

17
21
29
19
40

35
36
37
30
60

51
49
41
44
80

65
72
59
59
100

Динамическое программирование.

Условная оптимизация.

1-ый шаг. k = 4.

e3
u4
e4 = e3 - u4
f4(u4)
F*4(e4)
u4(e4)

20
0
20
0






20
0
11
11
20

40
0
40
0






20
20
11






40
0
19
19
40

60
0
60
0






20
40
11






40
20
19






60
0
30
30
60

80
0
80
0






20
60
11






40
40
19






60
20
30






80
0
44
44
80

100
0
100
0






20
80
11






40
60
19






60
40
30






80
20
44






100
0
59
59
100

2-ый шаг. k = 3.

e2
u3
e3 = e2 - u3
f3(u3)
F*3(e2)
F2(u3,e2)
F*3(e3)
u3(e3)

20
0
20
0
11
11
11
0



20
0
7
0
7




40
0
40
0
19
19






20
20
29
11
40






40
0
37
0
37
37
40

60
0
60
0
30
30








20
40
7
19
26








40
20
29
11
40
40
40



60
0
37
0
37






80
0
80
0
44
44








20
60
7
30
37








40
40
29
19
48








60
20
37
11
48
48
60



80
0
41
0
41






100
0
100
0
59
59








20
80
7
44
51








40
60
29
30
59








60
40
37
19
56






80
20
41
11
52






100
0
59
0
59
59

100

3-ый шаг. k = 2.

e1
u2
e2 = e1 - u2
f2(u2)
F*2(e1)
F1(u2,e1)
F*2(e2)
u2(e2)

20
0
20
0
11
11








20
0
16
0
16
16
20

40
0
40
0
37
37
37
0



20
20
16
11
27








40
0
21
0
21






60
0
60
0
40
40








20
40
16
37
53
53
20



40
20
21
11
32








60
0
36
0
36






80
0
80
0
48
48








20
60
16
40
56








40
40
21
37
58
58
40



60
20
36
11
47








80
0
49
0
49






100
0
100
0
59
59








20
80
16
48
64








40
60
21
40
61








60
40
36
37
73
73
60



80
20
49
11
60








100
0
72
0
72






4-ый шаг. k = 1.

e0
u1
e1 = e0 - u1
f1(u1)
F*1(e0)
F0(u1,e0)
F*1(e1)
u1(e1)

20
0
20
0
16
16
16
0



20
0
9
0
9






40
0
40
0
37
37
37
0



20
20
9
16
25








40
0
17
0
17






60
0
60
0
53
53
53
0



20
40
9
37
46








40
20
17
16
33








60
0
35
0
35






80
0
80
0
58
58








20
60
9
53
62
62
20



40
40
17
37
54








60
20
35
16
51








80
0
51
0
51






100
0
100
0
73
73
73
0



20
80
9
58
67








40
60
17
53
70








60
40
35
37
72








80
20
51
16
67








100
0
65
0
65





Смотрите также файлы