Файл: Отчет По лабораторной работе определение горизонтальной составляющей вектора индукции магнитного поля земли.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчеты по практике

Дисциплина: Не указана

Добавлен: 05.05.2024

Просмотров: 58

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Федеральное государственное бюджетное образовательное учреждение высшего образования «Кузбасский государственный технический университет имени Т.Ф.Горбачева»

Кафедра физики

Отчет

По лабораторной работе

«ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ»

Выполнил ст. группы: МАБз-211
Сарафанников М.А.

Проверил: _____________________
дата
Подпись

Допуск







отчет







Цель работы

1.Изучить метод определения горизонтальной составляющей вектора индукции магнитного поля Земли.

На рис. 1.1 приведена электрическая схема лабораторной установки, состоящая из тангенс-гальванометра G, амперметра А, реостата R, ключа К, двойного переключателя П и источника тока ε.

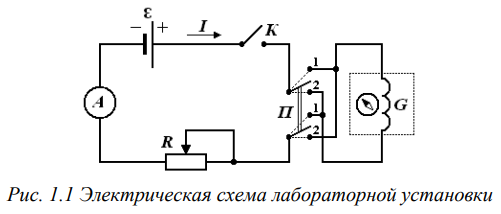
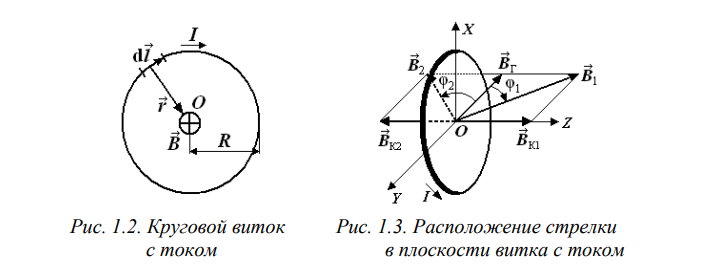
Тангенс-гальванометр G состоит из катушки, содержащей N витков тонкой изолированной проволоки, укреплённой на вращающейся подставке. В центре витков расположена магнитная стрелка, свободно вращающаяся вокруг вертикальной оси. 4 Стрелка помещена в коробочку, на дне которой расположен лимб со шкалой.



Основные расчётные формулы:












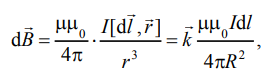
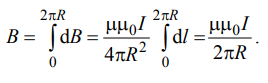
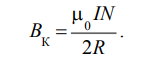
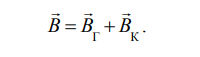
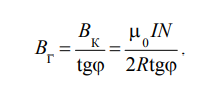
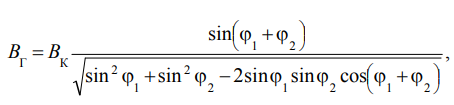
Таблица 1

Результаты измерений углов и расчета 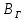при расположении витка в плоскости магнитного меридиана

№
I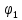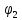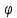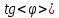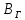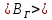




< >









дел
A
град
град
град



Тл
Тл

1
12
0,024
40
40












2
14
0,028
45
44












3
17
0,034
50
49












4
21
0,042
55
54













Таблица 2

Расчет измерений времени и расстояний L и расчет кинетических величин

ι
№ П/П
t


<ʋ>


<ω>
<ɛ>

M
с
с
м/с
м/с²
c-1
c-2

0,18
1
3,77
3,853
0,794
0,206
19,870
5,151

2
3,90

3
3,89

0,31
1
4,95
4,970
0,616
0,123
15,377
3,097

2
4,91

3
5,05

0,425
1
6,55
6,520
0,469
0,072
11,724
1,800

2
6,56

3
6,45


Таблица 3

Расчеты динамических характеристик поступательного движения

радиус шкива

масса

<а>
FH
<ʋ>
P
Ek₁
Eп

м
кг
м/с²
Н
м/с
кг*м/с
Дж
Дж

r₁
m₁=0,272
0,029
0,077
0,300
0,087
0,012
4,078

m₂=0,450
0,414
1,826
4,414
0,183
0,038

r₂
m₁=0,272
0,608
1,620
0,608
0,165
0,050
6,747

m₂=0,450
0,839
3,700
0,839
0,377
0,158


Таблица 4

Расчёт динамических величин вращательного движения


радиус шкива

масса

<ɛ>
<ω>
MH
J
L
Ek₂

м
кг
с-2
с-1
Н*м
кг*м2
кг*м2с-1
Дж

r1
m₁=0,272
2,264
15,773
0,001
0,000
0,006
0,040

m₂=0,450
2,942
21,702
0,035
0,011
0,239
2,590

r2
m₁=0,272
3,024
15,224
0,065
0,021
0,320
2,433

m₂=0,450
5,752
14,232
0,148
0,026
0,370
2,633



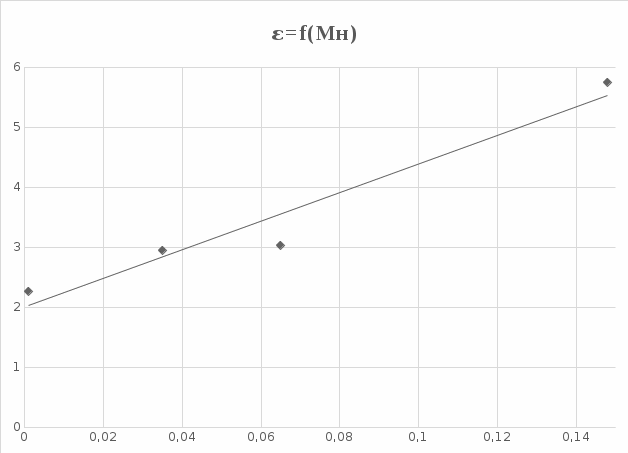График зависимости углового ускорения от модуля момента силы натяжения нити.
Таблица 5

Расчет момента энергии маятника при разных положениях грузов до оси вращения

 
ι
<ɛ>
Mн
J

м
с-2
Н*м
кг*м2

без грузов на спицах

—
5,752
0,148
0,026

с грузами на спицах
ι1 =0,18
5,151
0,173
0,033

ι2= 0,31
3,097
0,174
0,056

ι3= 0,425
1,800
0,175
0,097


График зависимости углового ускорения от момента инерции

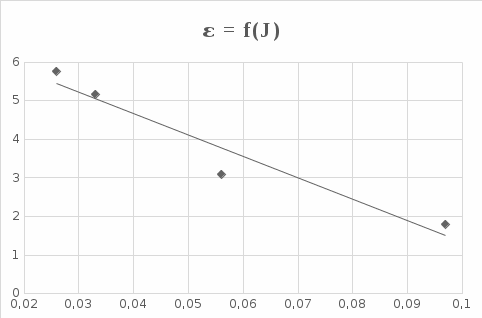
Вывод

В ходе данной лабораторной работы, на тему изучения поступательного и вращательного движения экспериментальным путём, с помощью маятника Обербека, находящимся под действием силы тяжести, натяжения нити и силы трения в подшипнике маятника, мы определили, что в конце движения груз имеет разную скорость, что сказывается на импульсе и его кинетической энергии.

Говоря о характере зависимости момента инерции маятника от его массы и от расстояния добавочных грузов до оси вращения можно выявить, что, изменяя положения цилиндров на стержнях маятника, (соблюдая их симметричное положение относительно оси вращения) можно проследить изменение величины момента инерции в зависимости от расстояния «
X» от оси вращения до цента цилиндра. При увеличении расстояния груза от оси момента инерции увеличивается. С увеличением массы груза так же увеличивается момент инерции. Согласно графику №1 угла ускорения от модуля момента силы натяжения нити, изменяя массу груза с одной и той же высоты, и изменяя время падения, момент инерции маятника увеличивается. По графику№2 можно увидеть, что выполняется основной закон динамики вращательного движения, чем больше угловое ускорение, тем меньше момент инерции.

Смотрите также файлы