Файл: Задача в 68 Обработка результатов равноточных многократных измерений 7 Вопрос 32 Требования, предъявляемые к органам по сертификации, испытательным лабораториям (центрам)..docx

Обработка результатов равноточных многократных измерений с получением среднего арифметического X, среднеквадратичного отклонения Sx, и определением суммарной погрешности измерения в виде доверительного интервала– ±ΣΔРд.

Исходные данные:

1	103,170	11	103,110	21	103,070	31	103,130	41	103,110	51	103,210
2	103,110	12	103,130	22	103,230	32	103,110	42	103,110	52	103,070
3	103,090	13	103,150	23	103,180	33	103,070	43	103,190
4	103,120	14	103,010	24	103,090	34	103,150	44	102,990
5	102,970	15	103,100	25	103,130	35	103,090	45	103,110
6	103,110	16	103,110	26	103,110	36	103,130	46	103,090
7	103,070	17	103,170	27	103,150	37	103,050	47	103,070
8	103,090	18	103,130	28	103,080	38	103,090	48	103,170
9	103,140	19	103,050	29	103,130	39	103,150	49	103,170
10	103,090	20	103,080	30	103,030	40	103,060	50	103,050

---

Цена деления прибора С, мм - 0,010

Результаты измерений, мм:

Доверительная вероятность Рд = 0,83 - показывает вероятность нахождения истинного значения в рассчитанном интервале.

Уровень значимости q = 0,01 - показывающий, что принятый закон рассеивания размеров не будет соответствовать реальному закону.

Сортируем значения по возрастанию:

1	102,97	11	103,07	21	103,09	31	103,11	41	103,15	51	103,21
2	102,99	12	103,07	22	103,09	32	103,11	42	103,15	52	103,23
3	103,01	13	103,07	23	103,10	33	103,12	43	103,15
4	103,03	14	103,08	24	103,11	34	103,13	44	103,15
5	103,05	15	103,08	25	103,11	35	103,13	45	103,17
6	103,05	16	103,09	26	103,11	36	103,13	46	103,17
7	103,05	17	103,09	27	103,11	37	103,13	47	103,17
8	103,06	18	103,09	28	103,11	38	103,13	48	103,17
9	103,07	19	103,09	29	103,11	39	103,13	49	103,18
10	103,07	20	103,09	30	103,11	40	103,14	50	103,19

---

1. Построение гистограммы

Определяем величину размаха R (поле рассеяния):

R = Xmax - Xmin=103,23-102,97=0,26

Xmax = 103,23- наибольшее из измеренных значений

Xmin = 102,97 - наименьшее из измеренных значений

R = Xmax - Xmin = 0,26 (мм).

Определяем число интервалов разбиения n

Вв соответствии с рекомендациями(ближайшее нечетное число)

n ===7,2?7.

Количество интервалов принимается ближайшим большим нечетным.

Принимаем n = 7.

Определяем ширину интервала h:



h ===0,037

Определяем границы интервалов Xmin - Xmax

1 интервал: Xmin1 - Xmax1

Xmin1 = Xmin=102,97 мм

Xmax1 = Xmin1 + h = 102,97+0,037=103,007 мм

2 интервал: Xmin2 - Xmax2

Xmin2 = Xmax1 = 103,007 (мм)

Xmax2 = Xmin2 + h = 103,007+0,037=103,044 (мм)

3 интервал: Xmin3 - Х max3

Xmin3 = Xmax2 = 103,044 (мм)

Xmax3 = Xmin3 + h = 103,044+0,037=103,081 (мм)

4 интервал: Xmin4 - Xmax4

Xmin4 = Xmax3 = 103,081 (мм)

Xmax4 = Xmin4 + h = 103,081+0,037=103,118 (мм)

5 интервал: Xmin5 - Xmax5

Xmin5 = Xmax4 = 103,118 (мм)

Xmax5 = Xmin5 + h = 103,118+0,037=103,155(мм)

6 интервал: Xmin6 - Xmax6

Xmin6 = Xmax5 = 103,155 (мм)

Xmax6 = Xmin6 + h = 103,155+0,037=103,192 (мм)

7 интервал: Xmin7 - Xmax7

Xmin7 = Xmax6 = 103,192 (мм)

Xmax7 = Xmin7 + h = 103,192+0,037=103,229=103,23 (мм)

Определяем середины интервалов Xoi

1 интервал:



Xo1 = Xmin1 + h/2=102,97 +0,0185=102,9885 (мм)

2 интервал:

Xo2 = Xmin2 + h/2 = 103,007+0,0185=103,0255 (мм)

3 интервал:

Xo3 = Xmin3 + h/2 = 103,044+0,0185= 103,0625 (мм)

4 интервал:

Xo4 = Xmin4 + h/2= 103,081+0,0185= 103,0995 (мм)

5 интервал:

Xo5 = Xmin5 + h/2 = 103,118+0,0185=103,1365 (мм)

6 интервал:

Xo6 = Xmin6 + h/2 = 103,155+0,0185= 103,1735 (мм)

7 интервал:

Xo7 = Xmin7 + h/2= 103,192+0,0185= 103,2105 (мм)

Определение количества размеров попадающих в каждый интервал mi

Используя заданную выборку, подсчитываем количество размеров попадающих в каждый интервал (если размер совпадает с границей интервала то его относят в интервал, находящийся слева по числовой оси).

Результаты выполненных выше расчетов занесем в таблицу:

Номер интервала	Границы интервала			Середина интервала Xoi (ММ)		Число размеров в интервале, mi
	Xmin (мм)	Xmax (мм)
1	102,97	103,007	102,9885		3		0,057
2	103,007	103,044	103,0255		3		0,057
3	103,044	103,081	103,0625		10		0,192
4	103,081	103,118	103,0995		18		0,346
5	103,118	103,155	103,1365		12		0,230
6	103,155	103,192	103,1735		4		0,076
7	103,192	103,23	103,2105		2		0,038

---

Используя табличные данные, строим гистограмму рассеивания единичных замеров и теоретическую кривую нормального распределения:



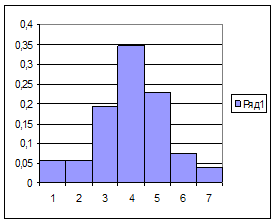
Рис. 1



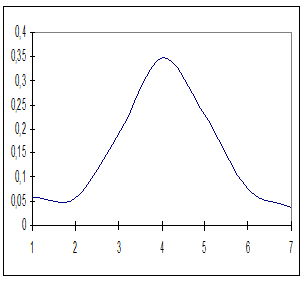
Рис. 2

2. Проверка выборки на соответствие нормальному закону распределения

При числе измерений свыше 50 проверка распределения на соответствие нормальному закону может выполняться по критерию Пирсона. При использовании этого критерия определяется параметр хи-квадрат по следующей формуле:



,

где Noi - теоретическая частота попадания в интервал.

Теоретическая частота попадания в интервал определяется по формуле:



ц(z) - плотность вероятности появления размеров в каждом интервале;

уx - среднеквадратичное отклонение размеров (СКО) выборки.

Считая, что СКО практически совпадает с его оценкой (уx ? Sx) приведем формулу, по которой определяется оценка СКО:



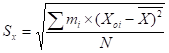
В данную формулу входит величина , которая представляет среднеарифметическое значение измеряемой величины и определяется по формуле:

 

X=1/52 x (103,9885 х 3 + 103,02553 х 3 + 103,0625 х 10 +103,0995 х 18 + 103,1365 х 12 + 103,1735 х 4 + 103,2105 х 2)=103,158

После подстановки 103,158 мм получим численные значения среднеарифметического и оценки СКО:

Sx=0,05 мм Х= 103,158 мм

Кроме полученных величин, для определения теоретической частоты попадания в интервал Noi необходимо знать плотность вероятности попадания размеров в каждом интервале.

Эту величину можно определить по формуле:



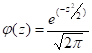
Так как расчеты по данной формуле достаточно сложны, значения плотности вероятности выбирают из таблицы в зависимости от безразмерного параметра Z, который для каждого интервала определяется по формуле:

---

Для 1 интервала:

Zo1 = -3,39 ,

что соответствует величине ц(z) = 0,012

Для 2 интервала:

Zo2 = -2,65

что соответствует величине ц(z) = 1,5

Для 3 интервала:

Zo3 = -1,91,

что соответствует величине ц(z) = 1,39

Для 4 интервала:

Zo4 = -1,17 ,

что соответствует величине ц(z) = 0,44

Для 5 интервала:

Zo5 = -0,43 ,

что соответствует величине ц(z) = 0,24

Для 6 интервала:

Zo6 = 0,03,

что соответствует величине ц(z) = 0,22

Для 7 интервала:

Zo7 = 1,05,

что соответствует величине ц(z) = 0,39

Определяем теоретические значения количества деталей для каждого интервала Noi.



Для 1 интервала:

No1 =0,46

Для 2 интервала:

No2 = 57,72

Для 3 интервала:

No3 =53,48

Для 4 интервала:

No4 =16,93

Для 5 интервала:

No5 = 9,23

Для 6 интервала:

No6 = 8,46

Для 7 интервала:

No7 = 15,007

На основании результатов измерений и расчета теоретических данных определяем фактическую и теоретическую частоту попадания размеров в интервал:

№ интервала	Фактическая чистота	Теоретическая чистота
1	0,057	0,025
2	0,057	0,097
3	0,192	0,222
4	0,346	0,295
5	0,230	0,226
6	0,076	0,100
7	0,038	0,025

Полученные результаты позволяют получить расчетную величину параметра хи-квадрат:

№ интервала	Фактическая частота	Теоретич. Частота
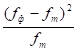1	0,057	0,025	0,025	0,00063	0,025
2	0,057	0,098	0,098	0,00960	0,098
3	0,192	0,22	0,227	0,05153	0,234
4	0,346	0,295	0,295	0,08703	0,295
5	0,230	0,226	0,217	0,04709	0,208
6	0,076	0,100	0,109	0,01188	0,118
7	0,038	0,025	0,031	0,00097	0,038

---