Файл: курсова ТПСПП_11111111111.doc

Загальна довжина N малих сходинок L дорівнює добуткові NL. При застосуванні до сніжинки Коха отримуємо невизначене число, коли L прямує до 0. Але таке означення не є задовільним, оскільки різні криві Коха мають різні розміри. Вихід полягає в тому, щоб вимірювати ані в метрах (m), ані в квадратних метрах (m²), але в деякому іншому ступені метра, m^x. Тепер 4N(L/3)^x = NL^x, оскільки втричі коротший відрізок потребує в 4 рази більше відрізків, як це видно з малюнку. Єдиним розв'язком цього рівняння є x = (log 4)/(log 3) ≈ 1.26186. Тому, одиниця вимірювання довжини межі сніжинки Коха дорівнює приблизно m^1.26186.

Генерування фракталів

Навіть збільшення в 2000 разів розкриває деталі множини Мандельброта, які відтворюють всю множину.

4 Застосування фракталів

Генерація зображень природних об'єктів

Геометричні фрактали застосовуються для отримання зображень дерев, кущів, берегових ліній тощо. Алгебричні та стохастичні — для побудови ландшафтів, поверхні морів, моделей біологічних та інших об'єктів.

Механіка рідин

Фракталами добре описуються такі процеси та явища, що стосуються механіки рідин і газів:

динаміка та турбулентність складних потоків;
моделювання полум'я;
пористі матеріали, у тому числі в нафтохімії.

Біологія

Моделювання популяцій;
біосенсорні взаємодії;
процеси всередині організму, наприклад, биття серця.

Фрактальні антени

Фрактальну геометрію для проектування антенних пристроїв було вперше застосовано американським інженером Натаном Коеном, який тоді жив у центрі Бостона, де було заборонено встановлювати зовнішні антени на будинках. Натан вирізав з алюмінієвої фольги фігуру у формі кривої Коха та наклеїв її на аркуш паперу, а потім приєднав до приймача. Виявилось, що така антена працює не гірше за звичайну. Й хоча фізичні принципи роботи

такої антени не вивчено досі, це не завадило Коену заснувати власну компанію й налагодити їхній серійний випуск.

Стиснення зображень

За допомогою фракталів можна стискати великі растрові зображення до частин їхніх нормальних розмірів. Це твердження випливає з теореми Банаха про стискуючі перетворення й є результатом роботи дослідника Технологічного інституту шт. Джорджія Майкла Барнслі.

Коротко метод можна описати таким чином. Зображення кодується кількома простими перетвореннями (в нашому випадкові афінними), тобто визначається коефіцієнтами цих перетворень (в нашому випадкові: A, B, C, D, E та F).

Наприклад, закодувавши якесь зображення двома афінними перетвореннями, ми однозначно визначаємо його за допомогою 12 коефіцієнтів. Якщо тепер задати яку-небудь початкову точку (наприклад, X = 0, Y = 0) та запустити ітераційний процес, то ми після першої ітерації отримаємо дві точки, після другої — чотири, після третьої — вісім і т. д. Через кілька десятків ітерацій сукупність отриманих точок описуватиме закодоване зображення. Але проблема полягає в тому, що дуже важко знайти коефіцієнти перетворень, які кодували б довільне зображення.

Не зважаючи на те, що було створено програмне забезпечення, що реалізує ці алгоритми (наприклад, бібліотеки фрактального стиснення використовуються в Microsoft Encarta), досить ефективного методу не було знайдено досі, а сам Майкл Барнслі продовжує працювати в даному напрямкові.

Децентралізовані мережі

Система призначення IP-адрес в мережі Netsukuku використовує принцип фрактального стиснення інформації для компактного зберігання інформації про вузли мережі. Кожен вузол мережі Netsukuku тримає лише 4 Кб інформації про стан сусідніх вузлів, при цьому будь-який новий вузол під'єднується до загальної мережі без необхідності в центральному регулюванні роздавання IP-адрес, що, наприклад, є характерним для мережі Інтернет. Таким чином, принцип фрактального стиснення гарантує повністю децентралізовану, а отже, максимально стійку роботу всієї мережі.

5 Дракон Хартера-Хейтуея(драконова ломана)

Для більшості регулярних фракталів фрактальна розмірність D менша, ніж розмірність d того простору, в якому знаходиться цей фрактальний об'єкт. Нерівність D < d відбиває факт некомпактності фрактала, причому чим більше розрізняються величини D і d, тим більше рихлим є фрактал.

Існують фрактали, які щільно заповнюють простір, в якому вони знаходяться, так що їх фрактальна розмірність D = d. Одним з прикладів такого роду є криві Пеано (Peano curves). Дракон Хартера-Хейтуэя є прикладом кривої Пеано, для якої область, яку вона заповнює на площині, має химерну форму. Перші чотири кроки його побудови представлено на мал. 3.2.

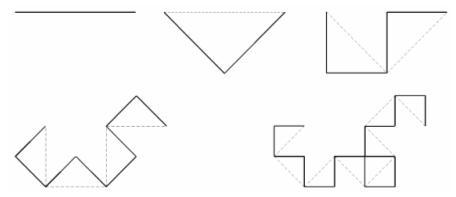
Малюнок 3.2 - Перші чотири кроки побудови дракона Хартера-Хейтуэя.

Як випливає з мал. 3.2 кожен з відрізків прямої на наступному кроці замінюється на два відрізки, що утворюють бічні сторони рівнобедреного прямокутного трикутника, для якого початковий відрізок був би гіпотенузою. В результаті відрізок як би прогинається під прямим кутом. Напрям прогину чергується. Перший відрізок прогинається управо (по ходу руху зліва направо), другий - вліво, третій - знову управо і так далі. На мал.3.2 пунктиром показана конфігурація попереднього кроку. Таким чином, після кожного кроку число наявних відрізків подвоюється, а довжина кожного відповідно зменшується в раз. Тому фрактальна розмірність утворюється в результаті (після нескінченного числа кроків) кривої рівна 2. [2, стор. 28-29].

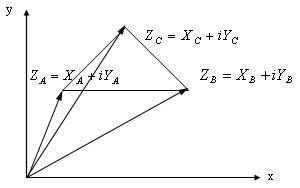Для реалізації вказаного вище алгоритму побудови необхідно перейти до комплексних чисел ZA, ZB і ZC (мал. 3.3).Малюнок 3.3 - Представлення в комплексних числах

Для знаходження координат точки C представимо комплексні числа в тригонометричній формі. Знаходження координат точки C представлене формулами (3.1) - (3.8).

(3.1) (3.2) (3.3) (3.4) (3.5) (3.6) (3.7) (3.8)

Р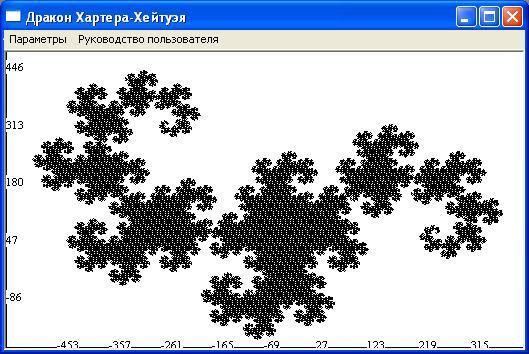езультатом реалізації приведеного вище алгоритму є програма, розроблена в середовищі Visual C++6.0. На мал. 3.4 представлено 16-е покоління дракона Хартера-Хейтуэя.

Малюнок 3.4 - Зображення 16-го покоління дракона Хартера-Хейтуея

6 Виконання роботи

Насамперед ми побудували базовий інтерфейс користувача. Для цього додали на форму наступні компоненти:

TPageControl з вкладки Win32 палітри компонентів.

Виділіть компонент TPageControl та виконайте наступну послідовність дій:

надали йому ім'я PageControl1 ;
задали властивості Align значення alClient, щоб компонент зайняв всю клієнтську область форми;
потім у властивості ActivePage створюємо 2 вкладки меню TabSheet: 1 називаємо «Драконова ломана» а іншу «Про програму»;
після цього наносимо на вкладку меню «Драконова крива» компонент Panel з вкладки Standard і ставимо властивість Align значення alClient, щоб компонент зайняв всю клієнтську область форми;
і наносимо компонент Image з вкладки Additional-сюди буде виводитися наш малюнок;
потім на цюж вкладку меню наносимо знову компонент Panel з вкладки Standard і ставимо властивість Align значення alleft, щоб компонент зайняв ліву частину клієнтської області форми;
вже на цю панель наносимо компонент Label з вкладки Standard і у властивості Caption пишемо «Сторін», наносимо компонент SpinEdit та наносимо компонент SpeedButton і відразу у властивості Caption пишемо
«намалювати» (ця кнопка служитиме нам для виводу нашого малюнку користувачу);
тепер на вкладку меню «Про програму» наносимо компоненти Label з вкладки Standard і у властивості Caption пишемо ім’я студента який розробив цю роботу,навчальний заклад а також тему.
вже після всього цього ми для компонента SpeedButton виконуємо процедуру procedure SpeedButtonClick в якій і пишемо частину прорами яка дозволить нам виводити наш малюнок.

Після всього цього ми пишемо код програми маючи інформацію про фрактали та драконову криву.

Коротка інформація про деякі кнопки використані в ході створення програми.

Компонент Button(SpeedButton)

Простою і, мабуть, найбільш часто використовуваною кнопкою є кнопка Button (см на мал. 5.1 у верхньому лівому кутку форми), розташована на сторінці бібліотеки Standard.

Основна з точки зору зовнішнього вигляду властивість кнопки - Caption (напис). У написах кнопок можна передбачати використання клавіш прискореного доступу, виділяючи для цього один з символів напису. Перед символом, який повинен відповідати клавіші прискореного доступу, ставиться символ амперсанта "&". Цей символ не з'являється в написі, а символ, що йде за ним, виявляється підкресленим. Тоді користувач може замість клацання на кнопці натиснути у будь-який момент клавішу Alt спільно з клавішею виділеного символу.