Файл: Устройство для получения хаотических колебаний или Генератор Хаоса своими руками.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.10.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Исследовательская работа
Устройство для получения хаотических колебаний
или
Генератор Хаоса своими руками
Авторы:
Бондаренко Иван Владимирович,
Сонец Денис Владимирович,
МАОУ лицей № 28, 11 класс,
г. Таганрог, Ростовская область.
Научный руководитель:
Дзюба Татьяна Владимировна,
учитель физики МАОУ лицея №28,
руководитель НОУ «СПЕКТР»
Таганрог, 2017 г.
Оглавление
Введение ....................................................................................................................3
-
Теоретическая часть.
-
Немного о хаосе……………………………………………...….……...4
-
Генератор Чуа……………………..……………....................................5
-
Математическая модель. Моделирование в Matlab…….….………....6
-
Практическая часть.
-
Результаты поэтапного моделирования……………………......……. 8
-
Макетирование……………………………………….…….…...............9
-
Порядок работы генератора Хаоса…………………….……………..10
-
Применение……………….…………………………….…………..….11
3. Выводы…………….……………………………………………………..……...12
4. Литература………………..…………………………………………….….….….13
5. Приложения….…………………………..……………………………...…….….14
Введение
У многих людей возникала идея управления происходящими вокруг хаотическими процессами: атмосферными явлениями, электромагнитными сигналами. Ведь это расширит возможности механики, авиации, электроники и даже биологии.
Как только мы стали углубляться в эту тему, поняли, что нам понадобится множество дополнительных знаний и навыков. Поэтому вместе со своим учителем физики стали осваивать новое направление - синергетика. Оказалось, хаос можно создать, а затем, применить на практике. Так возникла
Цель работы:
Создание генератора Хаоса.
-
Задачи:
-
познакомиться с теорией Хаоса;
-
рассмотреть математические методы моделирования физических систем;
-
создать виртуальную модель генератора Хаоса;
-
собрать работающий прототип генератора Хаоса и провести его испытания;
-
изучить хаотические колебания на примере генератора Чуа;
-
предложить способы применения устройства.
Методы исследования:
-
Анализ
-
Моделирование
-
Эксперимент
-
Обобщение
Объект исследования:
Генератор хаотических колебаний Чуа
Предмет исследования:
Хаотические колебания
-
Теоретическая часть
-
Немного о хаосе.
Говоря «хаос», мы, обычно, подразумеваем полное отсутствие порядка, абсолютную неупорядоченность и случайность. С математической точки зрения, хаос и порядок – понятия не взаимоисключающие. Теория хаоса (есть что-то завораживающие в названиях математических теорий) – достаточно молодая математическая область, создание которой приравнивают по значимости открытий ХХ века к созданию квантовой механики. Хаос случается в нелинейных динамических системах. Иначе говоря, любой процесс, который протекает со временем, может быть хаотичным (например, высота дерева, температура тела).
Чтобы разобраться, что такое хаос, сначала обратимся к системам, такой чертой не наделённым. Детерминированные системы не допускают никаких случайностей: значение на выходе полностью определено значениями на входе. Таким образом, изменение начальных условий вызывает пропорциональное изменение результата. Так, ньютоновская механика подразумевает детерминированность, и, изменяя, к примеру, силу удара по мячу, можно ожидать соответствующее изменение в продолжительности полёта этого мяча. Так что, по принципу детерминированности, положение мяча в текущий момент полностью определено положением мяча в предыдущий момент и будущее положение зависит от текущего и всё это совсем несложно посчитать. Предполагалось, что чем точнее известны начальные условия, тем точнее будет результат прогноза, однако известный математик Анри Пуанкаре, который занимался описанием орбит небесных тел, обнаружил, что в системах из 3-х и более тел, при незначительном изменение начальных условий (положения и скорости), траектории тела очень быстро удаляются друг от друга. Два близких набора начальных условий давали различные результаты.
Большой вклад в теорию хаоса внёс метеоролог Эдвард Лоренц. В шестидесятых годах прошлого века этот американец работал над компьютерной программой, моделирующей движение воздушных масс в атмосфере Земли. Все мы знаем, что компьютер (вопреки расхожим слухам) является строго детерминированной системой, и это создаёт известный принцип «garbage in garbage out». Лоренц гонял свою программу и в хвост, и в гриву, получая всякие разные результаты. Некоторые его коллеги даже делали предположения, что эта модель является точным предсказателем погоды, спрашивали, брать ли завтра зонтик. Разумеется, эти выводы были поспешны, вскоре выяснилась одна особенность модели погоды. Один раз для ускорения вычислений, Лоренц запустил программу не сначала, а ввёл в неё данные из предыдущего «прогона», которые были распечатаны на бумаге. Однако результаты такого запуска быстро начали отклоняться от уже полученных, формируя абсолютно другую картину. Немного неожиданно, не так ли? Оказалось, что Лоренц вводил не точные результаты прошлых вычислений, а округлённые перед выводом на печать, эта погрешность просто игнорировалась. Модель Лоренца оказалась сверхчувствительна к начальным условиям. Малейшее различие во входных данных приводило к сильному расхождению результатов с течением времени. Эта зависимость от начальных условий и была названа хаосом. Лоренцом была озвучена знаменитая черта хаоса, именуемая «эффектом бабочки», который предполагает, что в зависимости от того, махнёт ли бабочка крыльями в лесах Бразилии зависит случится ли в Техасе ураган или нет. Этот же принцип был положен в основу одноимённого фильма с Эштоном Катчером.[6]
Однако «хаос» и «случайность» понятия совсем не равнозначные. Определённая интерпретация процессов, кажущихся случайными, приводит их в порядок. К примеру, время между биениями сердца человека величина непостоянная, даже если человек не подвержен физической нагрузке. Если мы понаблюдаем за биением сердца некоторое время и интервалы между биениями запишем в таблицу, а также создадим второй столбец, копируя значения из первого, но со сдвигом на одно значение (т.е. первому измерению (t) в первом столбце будет соответствовать второе измерение (t+1) во втором, второму — третье и т.д.), можно будет построить карту, где по вертикали будем иметь значения без сдвига (t), а по горизонтали — значения со сдвигом(t+1). Точки на этой карте не будут рассыпаны в случайном порядке, а будут притянуты к некой области, формируя аттрактор.
Распространённый пример хаотической системы – это двойной маятник (рис 1), т.е. маятник, к концу которого прикреплен второй маятник. Вы, возможно, видели подобные маятники в магазинах подарков. Так вот если взять два одинаковых маятника, поставить рядом и отклонить их приблизительно на равную величину, то уже через несколько колебаний маятники полностью рассинхронизируются. Чем точнее мы будем соблюдать начальные условия, тем дольше маятники будут качаться в такт, однако от расходимости никуда не деться (приложение 1). [7]
-
Генератор Чуа.
По утверждению автора схемы, профессора Леона Чуа, широко известная теперь схема Чуа была придумана в 1983 г. после неудачного эксперимента с электронной моделью системы Лоренца. Автору схемы пришла в голову мысль, что поскольку основной механизм, приводящий к появлению хаоса в системах Лоренца и Ресслера — это наличие более чем одного неустойчивого положения равновесия (три для Лоренца и два для Ресслера), то можно придумать более простую систему, обладающую этими свойствами.
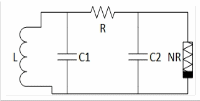
Его творение было гениально в своей простоте, цепь состояла из четырёх линейных элементов: двух конденсаторов, одной индуктивности и резистора, а также включала в себя один нелинейный локально активный элемент, на кусочно-линейной вольт-амперной характеристике которого имелась область с негативным сопротивлением, рисунок 2. Этот элемент теперь часто называют диодом Чуа. Цепь представляет собой генератор, и диод Чуа, который является необходимой частью для достижения хаотических колебаний.
Реализация диода Чуа возможна:
-
операционные усилители,
-
встречно-параллельно подключенные пара инверторов,
-
туннельный диод.
Принципиальная схема генератора Чуа (приложение №2).
-
Математическая модель. Моделирование в Matlab. [8]
Модель осциллятора Чуа описывается тремя дифференциальными уравнениями. В действительности это не так, математическая модель Чуа очень сложная, но обобщенный вид, который приводится во всех источниках, позволяет провести максимально точное моделирование осциллятора.
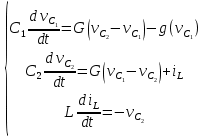 (1)
(1)
где 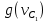 – кусочно-линейная функция определенная как:
– кусочно-линейная функция определенная как:
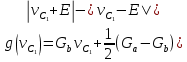
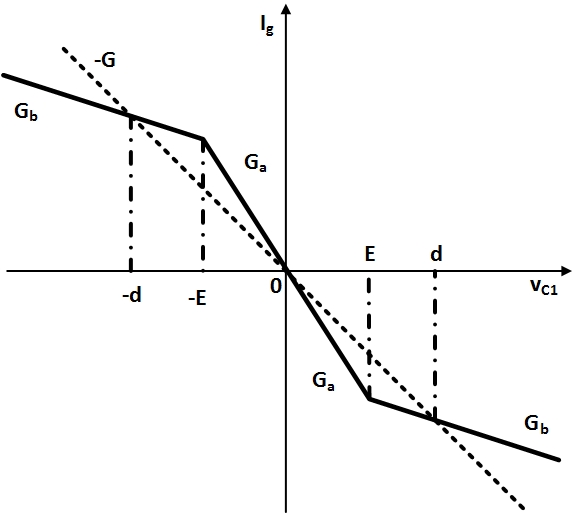
Эта нелинейная функция представлена графически на рисунке 3. Крутизна внутреннего и внешнего участков есть Ga и Gb, соответственно; при этом точки ±Е соответствуют изломам на графике (приложение 3).
Также показана нагрузочная прямая, от пересечения с которой образуются три точки равновесия d,0 и -d
Выполним следующие замены на безразмерные коэффициенты:
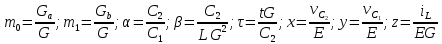
Система дифференциальных уравнений (1) можно переписать:
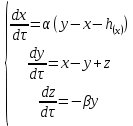 (2)
(2)
где 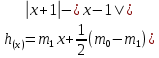
Моделирование системы (2) проводим среде Matlab. Так как основная цель моделирования достижение хаотического поведения, между номиналами элементов реальной модели должны соблюдаться определённые соотношения, которые были замены на безразмерные величины при переходе от системы (1) к системе (2):
-
ёмкость конденсатора С2 должна быть примерно 10 ёмкостей С1, 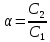 .
.
-
Коэффициент 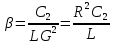 должен равняться приблизительно 15.
должен равняться приблизительно 15.
Файл функции Matlab:
function out = chua(t,in)
x = in(1);
y = in(2);
z = in(3);
alpha = 15.6;
beta = 28;
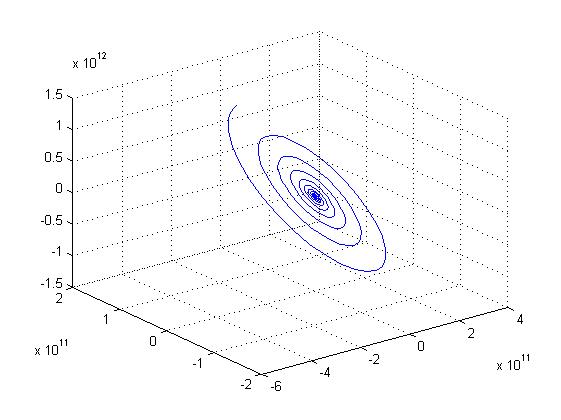
m0 = -2.185599971; %-1.143
m1 = -0.714;
h = m1*x+0.5*(m0-m1)*(abs(x+1)-abs(x-1));
xdot = alpha*(y-x-h);
ydot = x - y+ z;
zdot = -beta*y;
out = [xdot ydot zdot]';
Файл построения графиков Matlab:
[t,y] = ode45(@chua,[0 100],[0.7 0 0]);
plot3(y(:,1),y(:,2),y(:,3))
grid
-
Практическая часть
-
Результаты поэтапного моделирования:
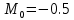
 Слабое проявление двух орбит
Слабое проявление двух орбит
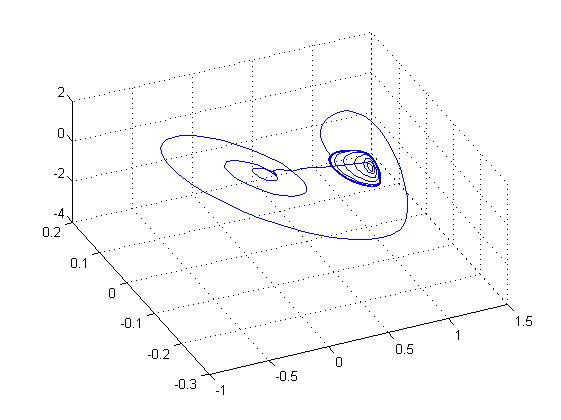
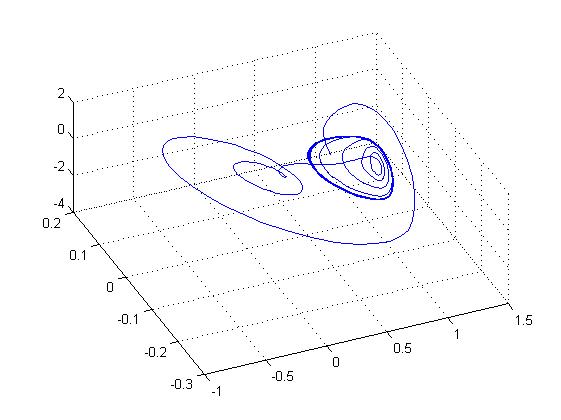
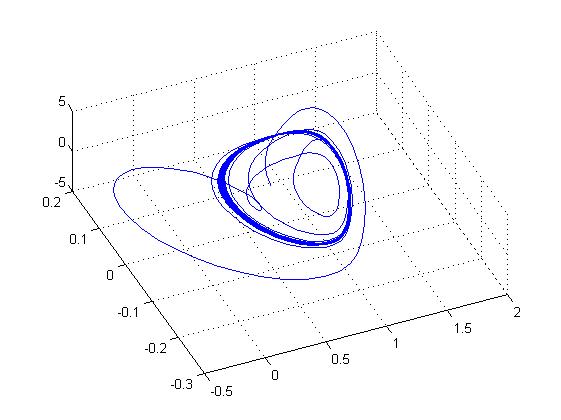
 Четкое проявление двух орбит, аттракторов
Четкое проявление двух орбит, аттракторов
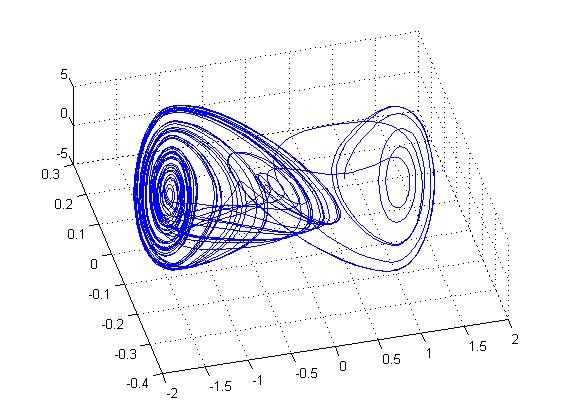
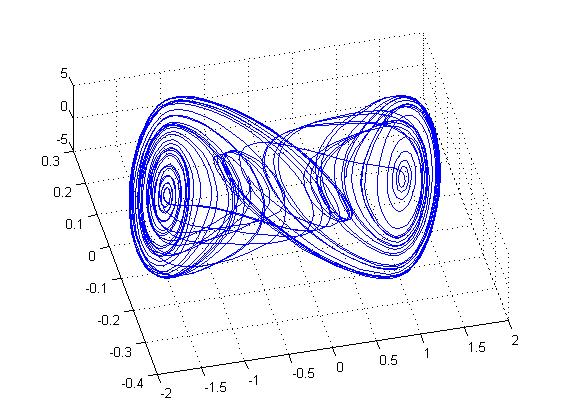
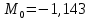 Математический хаос
Математический хаос
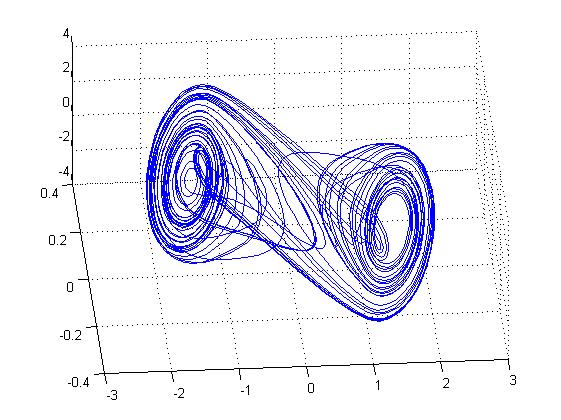
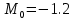
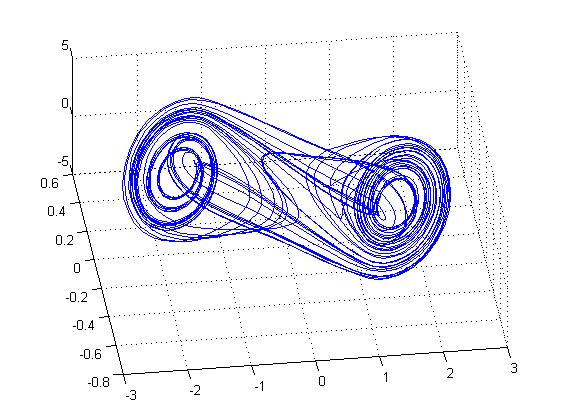
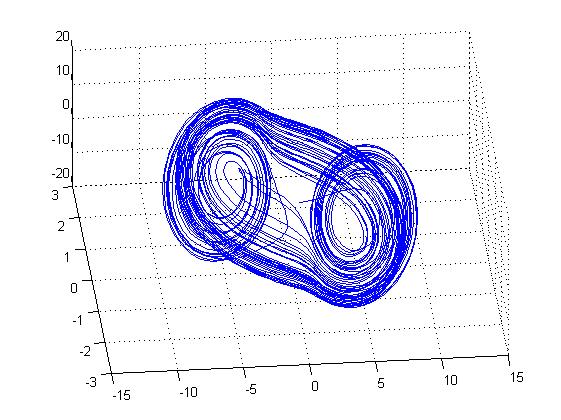
 Конец математического хаоса
Конец математического хаоса
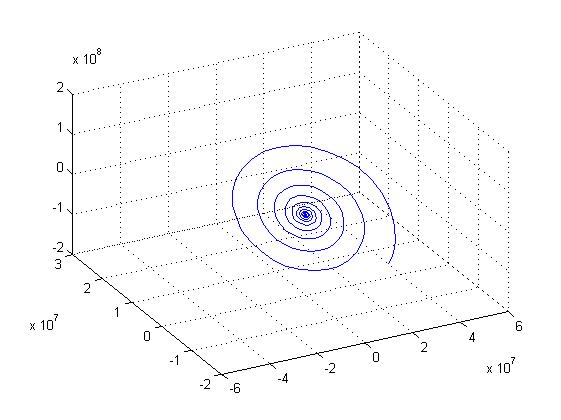
Математический хаос прекратился после добавления девятой цифры после запятой, что говорит о чувствительности генератора Чуа.
-
Макетирование
Современную схему генератора Чуа найти в интернете довольно таки просто. В классическом варианте, она состоит из двух конденсаторов, одной индуктивности, семи резисторов, микросхемы с парой операционных усилителей и двух батареек на 9В (можно использовать блок питания, но питание должно быть двухполярным) (приложение №4)
Схема предельно просто и приобрести для неё элементы в радиомагазине не составит труда. Но имеется ряд особенностей этой электрической схемы, с которыми я столкнулся при макетировании и которые никак не проявляются при моделировании в Matlab. К тому же в интернете их никто не оговаривает. Итак,
-
Организация диода Чуа выполнена на двух операционных усилителях в микросхеме TL082CP фирмы «Texas Instrument». С более простыми аналогами схема не работает.
-
Применять самые распространённые керамические конденсаторы нельзя. Подойдут майларовые или плёночные конденсаторы.
-
Не рекомендуется использовать потенциометры, слишком резкий ход. Предпочтительнее - построечные резисторы, легче регулировать хаос.
-
Основной вариант индуктивности, это применение готовой индуктивности, которая обязательно должна быть намотана на ферритовом сердечнике/кольце. Применение мною покупных индуктивностей не привели к успеху. Поэтому стал выбор или самостоятельно изготовить индуктивность (основная проблема, это необходимость выбирать между магнитной проницаемостью сердечника/кольца, количеством витков и сопротивлением обмотки), или замещение индуктивности сдвоенным операционным усилителем «U2» с обвязкой, научное название цепь гиратор. Важно микросхемы с операционными усилителями в диоде Чуа и в гираторе должны быть индентичными.
-
Прежде чем переходит к построению всей схемы необходимо сначала организовать правильное питание. В данном случае можно взять две батарейки и получить двух полярное питание, самое простое. Второй вариант источник питания двух полярного питания (приложение №5). Рекомендация при работе с готовой схемой питание на батарейках подключать самым последним. Садятся батарейки.
В итоге электрическая схема генератора Чуа приобрела вид (приложение №6).
Макет генератора хаоса представлен в приложении №7.
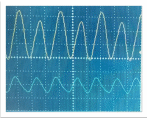
Наблюдение математического хаоса возможно при наличии осциллографа с двумя щупами и режимом «X-Y». Применение аналогового осциллографа предпочтительнее, чем цифрового.
-
Порядок работы:
• подсоединить щупы на штыревые разъемы с подписью на передней панели «X(Y)» и «Y(X)». Какой щуп будет «X» или «Y» не имеет значение,
• достаточно один «крокодил» любого щупа подсоединить к штыревому разъему с напдисью «GND». Обязательно подсоединять к контакту «GND», который находится рядом с «X(Y)» и «Y(X)». Подсоединение к «GND» внешнего питания создаст большие помехи,
• подать питание от батареек
• выбрать на осциллографе режим работы «X-Y»,
• по окончанию работы во избежание разряда батарей, извлечь их.
При работе вращать прямой отверткой головку винта обоих подстроечных резисторов. Вращать необходимо медленно. Если вы слышите щелчки при вращении головки винта подстроечного резистора, значит вы достигли крайнего положение. Измените направление вращения.
В результате работы, можно будет наблюдать осциллограммы, представленные в приложении №8.
-
Практическое применение.
Поскольку это генератор, значит, его можно использовать для радиосвязи, а раз этот генератор необычный, радиосвязь можно сделать защищённой. Существует несколько типов модуляции хаотического сигнала, от простого маскирования информационного сигнала, до высокоуровневой цифровой модуляции. Высокая чувствительность хаотического генератора позволяет использовать его в качестве детектора слабых сигналов. Также сообщалось о создании генератора случайных чисел на основе данной схемы. Кроме того, спектр данного генератора лежит в звуковом диапазоне, так что этой схемой не преминули воспользоваться концептуальные музыканты. К тому же лёгкость практической реализации, а также наличие относительно простой математической модели делает генератор Чуа удобной моделью при изучении теории хаоса.
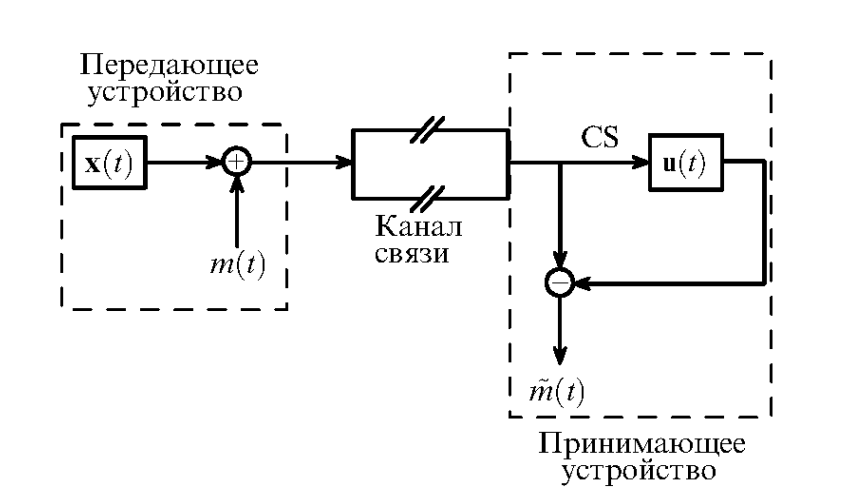
Хаотическая маскировка – один из наиболее простых способов скрытой передачи данных. Принципиальная схема реализации этого способа приведена в приложении №9.
На передающей стороне информационный сигнал m(t) подмешивается в сумматоре к несущему сигналу, генерируемому передающей хаотической системой x(t), и далее передается по каналу связи. В приёмнике осуществляется полная хаотическая синхронизация находящегося в нем хаотического генератора u(t) с помощью принимаемого сигнала, в результате чего динамика принимающего генератора становиться идентичной динамике передающего. Детектированный сигнал 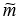 получается после прохождения через вычитающее устройство, как разность между принимаемым сигналом и синхронным откликом генератора хаоса в приемнике. [6],[7]
получается после прохождения через вычитающее устройство, как разность между принимаемым сигналом и синхронным откликом генератора хаоса в приемнике. [6],[7]
-
Выводы
Генератор Хаоса - простейший прибор, который дает возможность изучать хаос.
Простота в сборке и дешевизна данного прибора делаю его идеальным для применения военными. Высокая чувствительность к начальным условиям дает возможность использовать генератор Хаоса в качестве детектора даже самых слабых сигналов.
В обычной жизни его можно использовать как генератор случайных чисел или как необычный музыкальный инструмент.
В результате проведенной работы
её авторы
-
познакомились с основами синергетики, радиотехники, математическими методами моделирования;
-
создали устройство для визуализации Хаоса;
-
нашли применение генератору для хаотической маскировки в военных целях;
-
определили свою будущую профессию - инженера в области системного анализа и процессов управления.
-
учителя физики, экономики и математики начали разработку курса «Теория хаоса и сложных систем».
-
Литература
-
http://www.scholarpedia.org/article/Chua_circuit
-
https://en.wikipedia.org/wiki/Chua%27s_circuit
-
http://nonlinear.eecs.berkeley.edu/chaos/chaos.html
-
http://minitorn.tlu.ee/
jaagup/uk/dynsys/ds2/chaos/Case/Chua.html
Теоретическая часть.
-
Немного о хаосе……………………………………………...….……...4 -
Генератор Чуа……………………..……………....................................5 -
Математическая модель. Моделирование в Matlab…….….………....6
Практическая часть.
-
Результаты поэтапного моделирования……………………......……. 8 -
Макетирование……………………………………….…….…...............9 -
Порядок работы генератора Хаоса…………………….……………..10 -
Применение……………….…………………………….…………..….11
Задачи:
познакомиться с теорией Хаоса;
рассмотреть математические методы моделирования физических систем;
создать виртуальную модель генератора Хаоса;
собрать работающий прототип генератора Хаоса и провести его испытания;
изучить хаотические колебания на примере генератора Чуа;
предложить способы применения устройства.
Анализ
Моделирование
Эксперимент
Обобщение
Теоретическая часть
-
Немного о хаосе.
-
Генератор Чуа.
операционные усилители,
встречно-параллельно подключенные пара инверторов,
туннельный диод.
-
Математическая модель. Моделирование в Matlab. [8]
ёмкость конденсатора С2 должна быть примерно 10 ёмкостей С1,
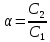 .
.Коэффициент
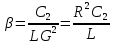 должен равняться приблизительно 15.
должен равняться приблизительно 15.-
Практическая часть
-
Результаты поэтапного моделирования:
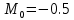

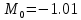 Слабое проявление двух орбит
Слабое проявление двух орбит
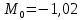

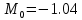

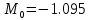 Четкое проявление двух орбит, аттракторов
Четкое проявление двух орбит, аттракторов
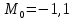

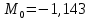 Математический хаос
Математический хаос
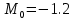

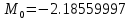

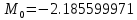 Конец математического хаоса
Конец математического хаоса
-
Макетирование
Организация диода Чуа выполнена на двух операционных усилителях в микросхеме TL082CP фирмы «Texas Instrument». С более простыми аналогами схема не работает.
Применять самые распространённые керамические конденсаторы нельзя. Подойдут майларовые или плёночные конденсаторы.
Не рекомендуется использовать потенциометры, слишком резкий ход. Предпочтительнее - построечные резисторы, легче регулировать хаос.
Основной вариант индуктивности, это применение готовой индуктивности, которая обязательно должна быть намотана на ферритовом сердечнике/кольце. Применение мною покупных индуктивностей не привели к успеху. Поэтому стал выбор или самостоятельно изготовить индуктивность (основная проблема, это необходимость выбирать между магнитной проницаемостью сердечника/кольца, количеством витков и сопротивлением обмотки), или замещение индуктивности сдвоенным операционным усилителем «U2» с обвязкой, научное название цепь гиратор. Важно микросхемы с операционными усилителями в диоде Чуа и в гираторе должны быть индентичными.
Прежде чем переходит к построению всей схемы необходимо сначала организовать правильное питание. В данном случае можно взять две батарейки и получить двух полярное питание, самое простое. Второй вариант источник питания двух полярного питания (приложение №5). Рекомендация при работе с готовой схемой питание на батарейках подключать самым последним. Садятся батарейки.
-
Порядок работы:
-
Практическое применение.
Выводы
познакомились с основами синергетики, радиотехники, математическими методами моделирования;
создали устройство для визуализации Хаоса;
нашли применение генератору для хаотической маскировки в военных целях;
определили свою будущую профессию - инженера в области системного анализа и процессов управления.
учителя физики, экономики и математики начали разработку курса «Теория хаоса и сложных систем».
Литература
http://www.scholarpedia.org/article/Chua_circuit
https://en.wikipedia.org/wiki/Chua%27s_circuit
http://nonlinear.eecs.berkeley.edu/chaos/chaos.html
http://minitorn.tlu.ee/
«Cellular Neural Networks, Multi-Scroll Chaos and Synchronization» Mustak E. Yalcin, Johan A. K. Suykens and Joos P. L. Vandewalle - World Scientific Series on Nonlinear Science, Series A - Vol. 50, Singapore, 2005
http://deadlock.org.ua/kit/habr/post/4476
http://bee.compkaluga.ru/forum/index.php?showtopic=65974
http://www.gpedia.com/ru/gpedia/%D0%A6%D0%B5%D0%BF%D1%8C_%D0%A7%D1%83%D0%B0
-
Приложения
Приложение №1.
Рисует лампочка на двойном маятнике. Художник Джордж Иоаннидис.

Приложение №2.
Принципиальная схема диода Чуа.
Приложение №3.
Вольт-амперная характеристика диода Чуа.
Приложение №4.
Классическая схема генератора Чуа.
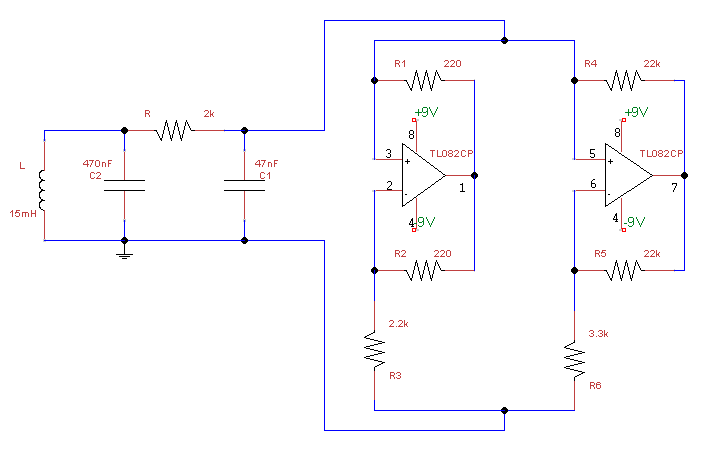
Приложение №5.
Схема организации двух полярного питания

Приложение №6.
Электрическая схема генератора Чуа.
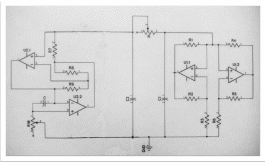
Приложение №7. Макет генератора Хаоса

Приложение №8.
Осциллограммы.
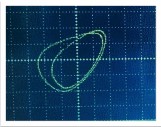
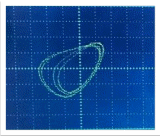


Приложение №9.
Принципиальная схема реализации хаотической маскировки.