Файл: Методическое пособие по практическим и лабораторным занятиям по дисциплине.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 16.10.2024

Просмотров: 49

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

20 кН




Из уравнения определяется реакция Rвх




Из уравнения определяется реакция Нву




Из уравнения определяется реакция Rav


Для контроля правильности решения используется дополни­тельное уравнение

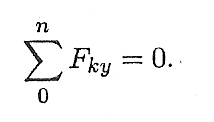
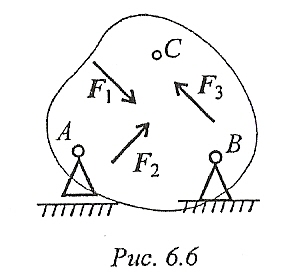
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):



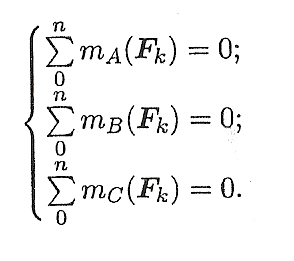
АЛГОРИТМ ВЫПОЛНЕНИЯ


  1. Заменяют распределённую нагрузку её равнодействующей

Для равномерно распределённой нагрузки равнодействующая равна произведению интенсивности нагрузки g на длину участка ℓ , на котором она действует G = gℓ

Перед решением задач рекомендуется уяснить и закрепить порядок нахождения равнодействующей и определения расстояний от неё до опор. При отсутствии навыков решения таких задач необходимо указывать положение равнодействующей относительно опор.

  1. Обозначают опоры

Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно – неподвижную и вторую шарнирно –подвижную опору.

  1. Освобождают от опор и заменяют их действие на балку реакциями.

В задачах на балку действуют только вертикальные нагрузки и сосредоточенные моменты. Реакции опор при нагрузке будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки) и обозначают реакцию опор А - RА, В – RВ

  1. Составляют уравнения равновесия вида: ΣМА = 0 , ΣМВ = 0

Напомним, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от этой точки приложения силы (в общем случае до линии действия силы).


Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать её момент положительным, а если против – отрицательным.

Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остаётся тем же, что для момента силы.

Выполняют проверку решения: Для этого составляют уравнение равновесия:

ΣFу= 0
Пример: Определить опорные реакции балки, изображённой на рисунке

Дано: g1 = 20 кН/м , g2 = 15 кН/м, М= 25 кНм, F= 30 кН


Рисунок

g 1 g2

A B

F

1м 3,5 м 1м 1,5м 1,5м

8,5 м
















Расчётная схема



RА Rв М

А В
G1 F G2
1 м 1,25м 2,25 м 1 м 1,5 м 1,5 м




Решение: 1. Заменяем распределённую нагрузку равнодействующей. На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдём равнодействующую.

G1 = g1 · 20 (1+3,5) = 90 кН, G2 = g2 · 15 (1,5+1,5) = 45 кН

2 Обозначим опоры А и В, Укажем опорные реакции RА, Rв

3. Составляем уравнения равновесия: ΣМА = 0 , ΣМВ
= 0

ΣМА = 0: G1 · 1,25 - F · 4,5 + G2 · 6 - Rв · 6 – М = 0

Rв · 6 = - G1 · 1,25 + F · 4,5 - G2 · 6 + М

Rв = - G1 · 1,25 + F · 4,5 - G2 · 6 + М / 6

Rв = 90 · 1,25 – 30 · 4,5 +45 · 6 – 25 / 6, Rв = 37,1 кН.

ΣМВ = 0: -М + F · 1,5 - G1 · 4,75 + RА · 6 = 0

RА · 6 = М - F · 1,5 + G1 · 4,75

RА = М - F · 1,5 + G1 · 4,75 / 6

RА = 25 - 30 · 1,5 + 90 · 4,75 / 6 RА = 67,9 кН.

5.Выполняем проверку, используя уравнение ΣFy= 0, которое примет вид

RА - G 1 + F + Rв - G2 = 0; 67,9 – 90 +30 +37,1 – 45 = 0

45 – 45 = 0; 0 = 0, реакции опор определены правильно.

Ответ: RА = 67,9 кН., Rв = 37,1 кН.

Задание Определить величины реакций в опорах балочных систем под действием сосредоточенных сил и распределенной нагрузки. Провести проверку правильности решения. Данные взять из таблицы 2, схема 2 - одноопорной балки (заделка) и таблицы 3, схема 3– для двухопорной балки с шарнирными опорами
Таблица 2

Исходные данные
вариант

1
2
3
4
5
6
7
8
9
10

№ схемы

1
2
3
4
5
6
7
8
9
10

Угол α0
55
75
30
18
25
65
75
45
39
27

a1,м
0,7
2
2,5
0,7
2,0
1,7
0,8
1,2
1,2
0,5

a2,м
0,8
0,6
0,5
2
4,5
0,3
2,2
1,2
0,8
1,3

a3,м
1,5
0,8
0,7
0,5
-
1,2
1,5
2,6
2,5
2,2


С 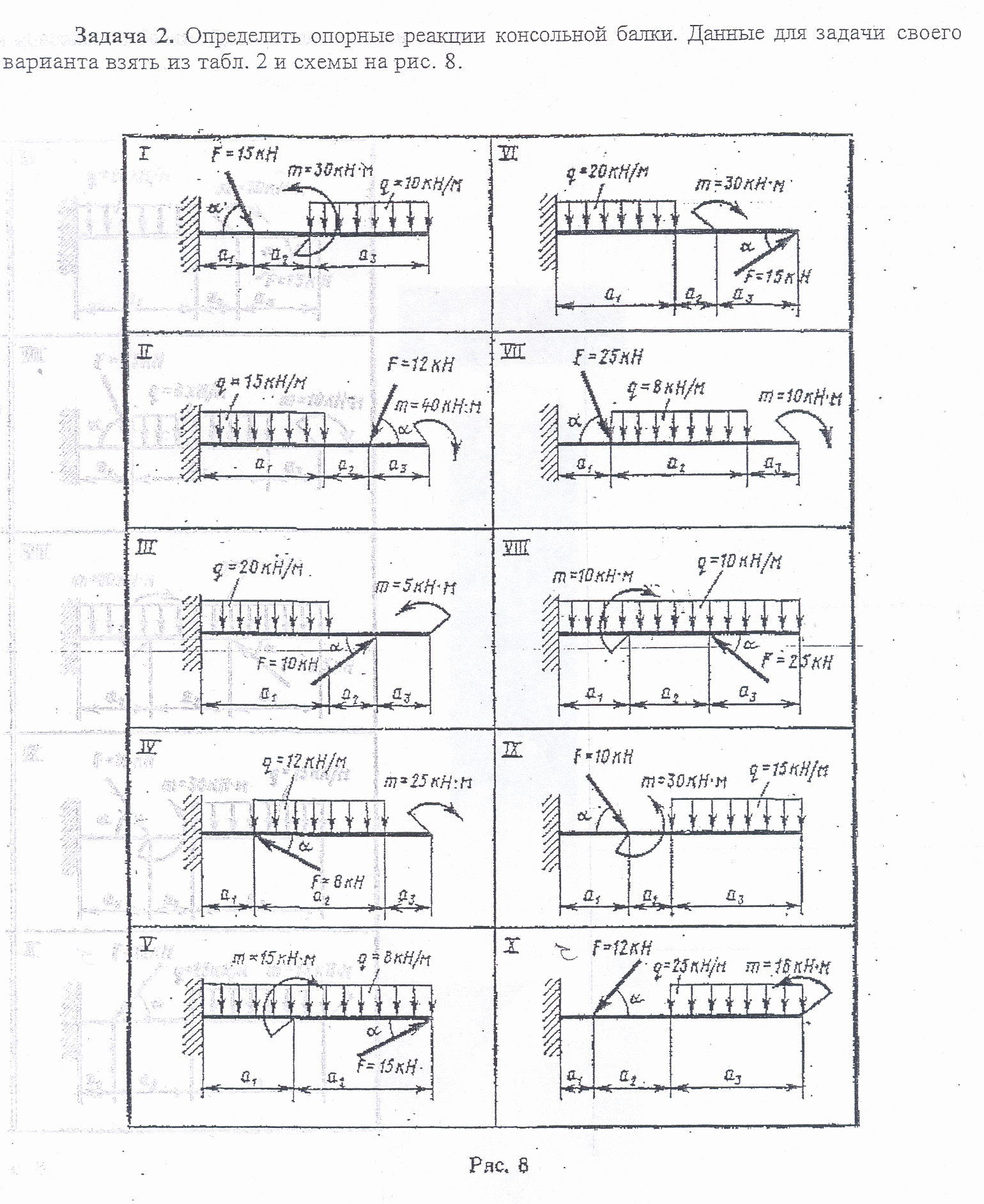хема 2

Таблица 3


Исходные данные
вариант

1
2
3
4
5
6
7
8
9
10

№ схемы

1
2
3
4
5
6
7
8
9
10

Угол α0
30
27
55
75
65
30
45
32
27
80

a1,м
1,2
2,5
1,5
3,0
1,2
1,1
1,2
1,5
1,8
1,5

a2,м
0,5
1,2
1,2
0,8
1,5
2,5
3,0
2,5
2,2
0,8

a3,м
0,8
0,8
2,5
1,2
1,5
0,7
0,5
1,5
0,7
1,5

а4,м
2,5
1,2
-
-
0,5
0,7
0,8
-
-
0,6

Смотрите также файлы