Задача №4.

Объем продаж компании Samsung в странах СНГ в I полугодии 1996г. составил 250 млн. долл. В целом же за год компания планировала реализовать товаров на 600 млн. долл. Вычислите относительный показатель плана на II полугодие.
Решение:

Плановый объем продаж на второе полугодие

П₂­ = П – П₁ = 600 – 250 = 350 млн. долл.,

где П – план на год, П₁– объем продаж в первом полугодии.

Относительный показатель плана

ОП_пл= П₂/ П₁* 100% = 350 / 300 * 100% = 116,7%

Вывод. Во втором полугодии компания планирует увеличить объем продаж на 16,7% по сравнению с первым полугодием.

Задача №5.

Предприятие планировало увеличить выпуск продукции в 1997г. по сравнению с 1996г. на 18%. Фактический же объем продукции составил 112,3% от прошлогоднего уровня. Определите относительный показатель реализации плана.
Решение:

В этой задаче плановое задание выражено в виде прироста уровня в планируемом периоде, где оно сравнивается с уровнем базисного периода. В этом случае относительная величина выполнения плана определяется из процентного сопоставления коэффициента фактического роста явления с плановым коэффициентом:



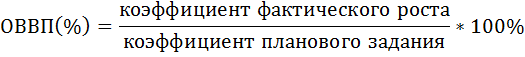
Заданный планом прирост выпуска продукции (18%) выражаем в форме коэффициента роста выпуска продукции в 1997г. по сравнению с 1996г.:

1 + 0,18 = 1,18.

Фактический процент роста выпуска продукции (112,3%) выражаем в форме коэффициента:

112,3 / 100 = 1,123.

С помощью полученных коэффициентов рассчитываем относительную величину выполнения плана.

ОВВП (%)=1,123/1,18*100%=95,17

Таким образом, в 1997 г. плановое задание по выпуску продукции не выполнено на 4,83%.

Задача №6.

Имеются следующие данные о производстве бумаги в РФ

Год.	1992	1993	1994	1995
Произведено бумаги, тыс. т	3603	2882	2215	2771

Вычислите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь.

---

Решение:

Относительная величина (показатель) представляет собой отношение уровня исследуемого явления или процесса за данный период к уровню этого же процесса или явления в прошлом.

Относительная величина динамики характеризует интенсивность, структуру, динамику экономических явлений, показывает во сколько раз текущий уровень превышает предшествующий. (базисный). Величина динамики называется коэффициентом роста, если выражена кратным соотношением или темпом роста, если выражена в %.

Год	Производство бумаги, тыс.т.	Показатели динамики с переменной базой, %	Показатели динамики с постоянной базой, %
1992	3603	100	100
1993	2882	79,99	79,99
1994	2215	76,86	61,48
1995	2771	125,10	76,91

Показатели динамики с переменной базой:

Относительная уровень показ-ля каждого периода

величина = ________________________________ *100%

динамики (перем) предшествующий уровень

2882/3603*100=79,99%

2215/2882*100=76,86%

2771/2215*100=125,10%

Показатели динамики с постоянной базой:

Относительная уровень показ-ля каждого периода

величина = ________________________________ *100%

динамики (постоян) первоначальный уровень

3603/3603*100=100%

2882/3603*100=79,99%

2215/3603*100=61,48%

2771/3603*100=76,91%

Взаимосвязь между базисными и цепными показателями динамики:

1. 
   Произведение всех относительных величин с переменной базой сравнения равно относительной величине с постоянной базой сравнения за исследуемый период.
   

0,7999х0,7686х1,251=0,769

2. 
   Отношение последующей величины динамики с постоянной базой к предыдущим показателям динамики с постоянной базой равно соответствующей величине динамики с переменной базой сравнения.
   

0,7690/0,6148=1,251

Задача №7.

Добыча нефти и угля в РФ во II квартале 1996г. характеризуется следующими данными:

Топливо	Объем добычи, млн.т.
	Апрель	Май	Июнь
Нефть	23,8	25,0	24,2
Уголь	23,2	20,2	18,7

---

Теплота сгорания нефти равна 45,0 мДж/кг, угля - 26,8 мДж/кг. Сделайте пересчет в условное топливо (29,3 мДж/кг) и проведите анализ изменения совокупной добычи этих ресурсов.

Решение:

Определим коэффициенты пересчета в условное топливо:

Для нефти = 45/29,3=1,5358

Для угля = 26,8/29,3=0,9147

С учетом пересчета:

23,8х1,5358=36,55; 25х1,5358=38,40; 24,2х1,5358=37,17

23,2х0,9147=21,22; 20,2х0,9147=18,48; 18,7х0,9147=17,10

Топливо	Объем добычи, млн.т.
	Апрель	Май	Июнь
Нефть	36,55	38,40	37,17
Уголь	21,22	18,48	17,10

По исходным данным:

Добыча нефти за 3 месяца: 23,8+25+24,2=73

Добыча угля за 3 месяца: 23,2+20,2+18,7=62,1

73/62,1х100=117,55%

Угля добыто на 55% больше, чем нефти.

С учетом перерасчета:

Добыча нефти за 3 месяца: 36,55+38,4+37,17=112,12

Добыча угля за 3 месяца: 21,22+18,48+17,10=56,80

112,12/56,80х100=197,39%

После перерасчета на условное топливо, при сравнении двух совокупностей ресурсов, превышение добычи нефти на 97,39%.

Задача №8.

В апреле 1996г. прожиточный минимум для трудоспособного населения составил 419,0 тыс. руб. в месяц на человека, для пенсионеров - 262,5 тыс. руб., для детей - 376,1 тыс. руб. Сделайте выводы о соотношении этих величин, используя относительные показатели сравнения.

419/262,5=1,6 419/376,1=1,1 376,1/262,5=1,43

Прожиточный минимум для трудоспособного населения в 1,6 раза больше, чем для пенсионеров и в 1,1 раза больше, чем для детей. Прожиточный минимум для детей в 1,43 раза больше, чем для пенсионеров.

Задача №9:

Известно распределение работников предприятия по возрасту:

Возраст, лет	Число работников, в % к итогу	Накопленная частота
до 25	14.0	14
25-35	22.0	36
35-45	20.0	56
45-55	17.0	73
55-65	15.0	88
65 и старше	12.0	100

---

Определите средний возраст работника,  рассчитайте моду и медиану

Первый способ.

Сначала найдем средний возраст рабочих по группе:

1) 20

2) (25+35) : 2 = 30

3) (35+45) : 2 = 40

4) (45+55) : 2 = 50

5) (55+65) : 2 =60

6) 70

(делим на два, так как 2 возраста, складывали 2 элемента, значит чтобы найти средний возраст надо сложить возрасты и поделить сумму на их количество, то есть 2).

Затем средний возраст групп умножаем на количество работников, чтобы найти общий возраст каждой группы:

1) 20*14=280

2) 30*22=660

3) 50*17=850

4) 60*15=900

5) 70*12=840

Теперь складываем общий возраст:

280+660+800+850+922+840=4330

Складываем количество работников каждой группы :

14+22+20+17+15+12=100

Делим общий возраст на общее количество работников:

4330/100=43,3 примерно 45 лет средний возраст работника

Это примерно 40-50

Второй способ.

Нужно просто сложить средние возрасты каждой группы и поделить на количество групп:

(20+30+40+50+60+70)/6=45

Ответ: 40-50 года ; 45 лет - средний возраст работника

Модальный интервал находится в пределах возрастной группы 25-35 лет, так как на этот интервал приходится наибольшая частота (22).

Рассчитаем величину моды:



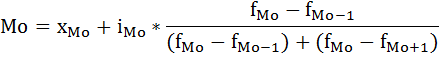
Мо = 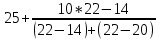=28 лет

Это значит, что модальный возраст работников равен 28 годам.

Рассчитаем величину медианы.



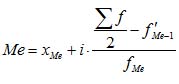
Для нахождения медианного интервала нужно знать половину частот, т.е 100/2=50. В столбце «накопленные частоты» выбираем 3 интервал, т.к во 2 интервале частот меньше половины. С помощью формулы найдем конкретное значение медианы, оно принадлежит медианному интервалу 35-45

Ме = 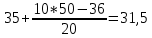лет

Это значит что одна половина работников имеет возраст до 31,5 года, а другая свыше 31,5 года.

Задача №10.

По следующим данным определите, в каком семестре уровень успеваемости студентов потока был выше:

Балл	Число студентов
	1 семестр	2 семестр
"2"	6	8
"3"	32	20
"4"	24	36
"5"	18	16

---

Решение:

Рассчитаем средний балл студентов за 1 семестр по формуле средней арифметической взвешенной.





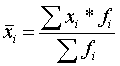
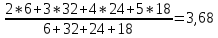
Теперь рассчитаем средний балл студентов за 2 семестр:



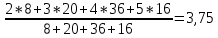
Ответ: во 2 семестре средний балл составляет 3,75 против 3,68 в 1 семестре.

Задача №11.

Имеются следующие данные о дневной реализации помидоров на рынках города:

Рынок	Объем реализации (руб.)	Средняя цена 1 кг (руб.)
1	4200	12
2	5880	14
3	10500	15

Вычислите среднюю цену 1 кг помидоров в целом по всем рынкам города

Решение:

Вычислим среднюю цену за 1 кг помидоров по формуле




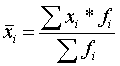
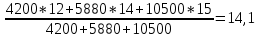
Ответ: средняя цена за 1 кг помидоров по всем рынкам города равна 14 руб.

Задача №12.

По трем районам города имеются следующие данные на конец года

Район	Число отделений сбербанка	Среднее число вкладов в отделении	Средний размер вклада, руб.
1 2 3	4 9 5	1376 1559 1315	275 293 268

Решение:

Для определения среднего размера вклада в Сбербанке используем исходное соотношение средней (ИСС):



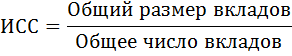
Определим общее число вкладов, умножив число отделений на среднее число вкладов в отделении:

---

Смотрите также файлы

• Типы полевых жилищ, их гигиеническая оценка.docx

• Климат Климаты Земли весьма многообразны. Поэтому их классифицируют, т е. выделяют разные типы, и на их основе осуществляют климатическое районирование..docx

• 1 Страхователи для неработающих граждан это органы исполнительной власти субъектов рф.doc

• 78 сынып оушыларына арналан жасспірімдер арасындаы жаратылыстану математикалы баыттаы облысты олимпиада Областная юниорская олимпиада естественноматематического цикла среди учащихся 78 классов Павлодар, 2013.docx

• Правовой статус Содружества был закреплён Вестминстерским.docx