Файл: Пояснительная записка к курсовой работе по дисциплине Радиотехнические цепи и сигналы.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ

УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ радиотехники (ТОР)


ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ
И ЦИФРОВАЯ ФИЛЬТРАЦИЯ
Пояснительная записка к курсовой работе

по дисциплине «Радиотехнические цепи и сигналы»
Вариант 39

Выполнил: студент гр. З-161П12-5 Сайфидинов Ж. Ж.

«___»______________ 2023 г.


Проверила: Попова А.И.

«___»______________ 2023 г.
Томск 2023

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ радиотехники (ТОР)
ЗАДАНИЕ

на курсовую работу по дисциплине «Радиотехнические цепи и сигналы»
«ДИСКРЕТНАЯ ОБРАБОТКА СИГНАЛОВ
И ЦИФРОВАЯ ФИЛЬТРАЦИЯ»
Студенту Сайидинову Ж. группа 3-161П12-5

1. 
   Исходные данные:
   

1.1 Номер варианта – 39
1.2 Модель аналогового сигнала

Шифр N1N2	График сигнала
11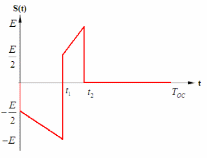

1.3 Временная структура аналогового сигнала

Шифр N3N4	t1	t2	t3	TOC
07	70 мкс	1,5t1	2,5t1	3,5t1

1.4 Модель линейной электрической цепи (аналогового фильтра-прототипа)

Шифр N5N6	Модель линейной электрической цепи
07

---

1.5 Задание варианта цифрового фильтра

Шифр N7N8	Тип аппроксимации АЧХ (наименование окна)	Метод синтеза цифрового фильтра	Тип импульсных характеристик	Тип ЦФ
05	Бартлетта	Метод частотной выборки	КИХ (ТЦФ)	ФНЧ

1.6 Параметры затухания А_П и А_З АЧХ цифровых ФНЧ и нормированные граничные частоты полос пропускания 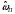и заграждения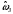

Шифр N9N10	Неравномерность (АП) АЧХ в пределах полосы пропускания, дБ	Затухание (АЗ) АЧХ в полосе заграждения, дБ	Нормированные граничные частоты полос пропускания и заграждения
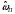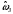18	1,0	15	0,1	0,15

2. 
   Задание
   

1. 
   Задание на первую часть курсовой работы
   

1. 
   Дискретизировать заданный шифром N₁N₂ сигнал и восстановить аналоговый сигнал, используя ряд Котельникова. При определении наивысшей частоты спектра сигнала использовать пороговый критерий
   (для f>f_max амплитуды спектральных составляющих, не превышают уровня 0,1 от максимальной).
   
2. 
   Рассчитать спектр дискретной последовательности, определенной в пункте 2.1.1. Построить график.
   
3. 
   Найти Z-преобразование найденной в п. 2.1.1 дискретной последовательности.
   
4. 
   Определить дискретное преобразование Фурье (ДПФ)той же дискретной последовательности. Построить график. Восстановить аналоговый сигнал, используя тригонометрический ряд Фурье.
   
5. 
   По результатам пункта 2.1.4 найти исходную дискретную последовательность. Построить график.
   
6. 
   Произвести сравнение результатов вычислений:
   

1) сравнит форму спектра дискретизированной последовательности со спектром исходного аналогового сигнала;

---

2) установить связь между:

а) результатом Z-преобразования и спектральной плотностью дискретной последовательности;

б) между спектром исходного периодического аналогового сигнала и дискретными отсчетами его спектральной плотности.

2. 
   Задание на вторую часть курсовой работы Вариант I
   

1. 
   Для заданной шифром N₅N₆ аналоговой линейной электрической цепи найти операторное выражение передаточной функции К(р) и импульсную характеристику g(t).
   
2. 
   Осуществить синтез цифровой цепи методом билинейного
   Z-преобразования по найденной в п. 2.2.1 К(р). Построить схему алгоритма цифрового фильтра (ЦФ).
   
3. 
   Произвести синтез ЦФ с помощью метода инвариантности импульсной характеристики (ИИХ) по найденной в пункте 2.2.1 g(t). Построить схему алгоритма ЦФ.
   
4. 
   Найти отклик ЦФ в виде выходной дискретной последовательности на входную дискретную последовательность, полученную в пункте 2.1.1, на основе выполнения пунктов 2.2.2 или 2.2.3 с помощью обратного
   Z-преобразования либо с помощью алгоритма свертки (по выбору студента).
   
5. 
   Сделать выводы о сравнении методов синтеза по трудоемкости, сложности конечного результата, о физической достоверности полученной формы отклика в реальных условиях прохождения дискретного сигнала через синтезированную цепь.
   

2. 
   Задание на вторую часть курсовой работы Вариант II
   

1. 
   Синтезировать заданный шифром N₇N₈ цифровой фильтр с бесконечной (БИХ) или конечной (КИХ) импульсной характеристикой требуемого назначения: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ) или режекторный фильтр (РФ).
   

Метод синтеза цифрового фильтра, тип аппроксимации частотной характеристики (АЧХ) и наименование оконной функции также заданы шифром N₇N₈.

Параметры затухания А_П и А_З, характеризующие неравномерность АЧХ цифровых фильтров и нормированные граничные частоты полос пропускания и заграждения заданы шифром N₉N₁₀.

2. 
   Рассчитать частотные (амплитудно-частотную и фазочастотную) характеристики синтезированного цифрового фильтра.
   
3. 
   Рассчитать временные (импульсную и переходную) характеристики синтезированного фильтра.
   
4. 
   Определить вид дискретного сигнала на выходе фильтра при воздействии на его вход последовательности отсчетов заданного входного сигнала x(t).
   

---

Руководитель проекта

(Ф.И.О., должность, место работы)


Задание принял к исполнению

(дата, подпись студента)
СОДЕРЖАНИЕ

Введение

Целью данной курсовой работы является практическое освоение методов анализа аналоговых и дискретных сигналов во временной и частотной областях, а также расчет цифровых фильтров на примере решения конкретной задачи.

Применение в радиоэлектронике цифровой обработки сигналов позволяет решать задачи, которые невозможно осуществить аналоговыми методами. Также при синтезе в цифровой форме можно достичь лучших характеристик аналоговых устройств-прототипов.

Курсовая работа состоит из двух частей.

Первая часть представляет собой спектральный анализ аналогового сигнала, его дискретизацию и спектральный анализ дискретного сигнала.

Вторая часть содержит синтез цифровых фильтров.

1. Спектральный анализ аналогового сигнала

   1. Исходные данные

Временные интервалы, характеризующие исходный аналоговый сигнал, приведены в таблице 1.1.

Таблица 1.1

Интервал описания фрагмента сигнала t1, мкс	Интервал описания фрагмента сигнала t2, мкс	Период описания сигнала, ТОС, мкс
70	105	245

---

Входное напряжение примем равным Е=10 В;

Циклическая частота сигнала.

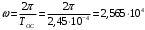рад/с.

Временное представление исходного аналогового сигнала сложной формы приведено на рисунке 1.1.


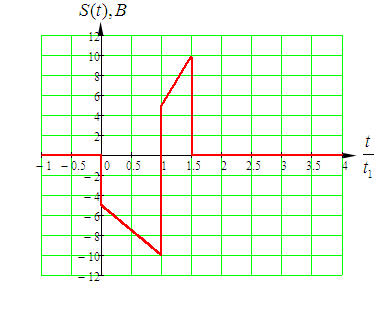
Рисунок 1.1 – Временное представление аналогового сигнала сложной формы (время нормировано относительно t₁₎

2. Расчет спектральной плотности аналогового сигнала

Для упрощения расчета спектральной плотности мощности с помощью преобразования Лапласа исходя из временного представления сигнала (рисунок 1.1), разложим сигнал на типовые составляющие, включающиеся в определенный момент времени. При разложении используем единичную функцию включения (t) [1].

Сигнал можно разложить на следующие типовые составляющие:

;

;

;

;

;

.

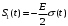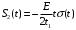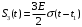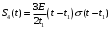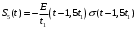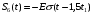Исходный аналоговый сигнал представляет собой сумму типовых составляющих

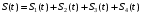, (1.1)

Временное представление типовых составляющих исходного аналогового сигнала приведено на рисунке 1.2.



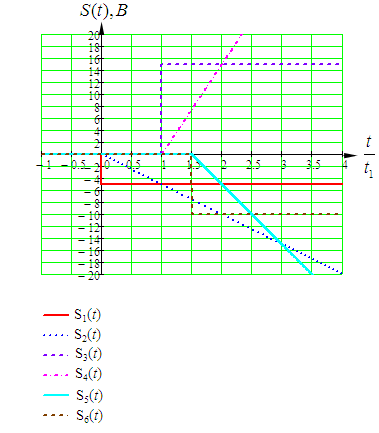
Рисунок 1.2 – Временное представление типовых составляющих аналогового сигнала (время нормировано относительно t₁₎
Для расчета спектральной плотности аналогового сигнала, применим прямое преобразование Лапласа к его типовым составляющим [2]. Изображение типовых составляющих исходного аналогового сигнала:

;

;

;

;

;

.

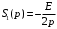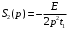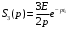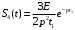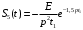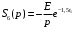Изображение исходного аналогового сигнала представляет собой сумму изображений его типовых составляющих

---