ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая профессиональная образовательная организация «Многопрофильная Академия непрерывного образования»
(АНПОО «МАНО»)
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПО ДИСЦИПЛИНЕ
Математика
ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
2021
СОДЕРЖАНИЕ
| Раздел 1 Теория пределов Тема 1.1 Предел функции в точке…………………………………………………..3 Раздел 2 Дифференциальное исчисление Тема 2.1 Производная функции………………………………………………….....7 Раздел 4 Применение элементов дифференциального и интегрального исчисления при решении прикладных задач……………………………………..10 Раздел 7 Элементы теории комплексных чисел………………………………….17 |
Раздел 1 Теория пределов
Тема 1.1 Предел функции в точке
Практические занятия №1 Вычисление пределов функции в точке
Цель работы:
На конкретных примерах научиться вычислять пределы различными способами.
Содержание работы:
Типы неопределенностей и методы их раскрытия
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.
I. Неопределенность вида
Пример 1. Вычислить предел
Решение: При подстановке вместо переменной х числа 5 видим, что получается неопределенность вида
-25 = (х-5)*(х+5), получили общий множитель (х-5),на который можно сократить дробь. Заданный предел примет вид:
Пример 2. Вычислить предел
Решение: При подстановке вместо переменной х числа 3 видим, что получается неопределенность вида

II. Неопределенность вида
Пример 4. Вычислить предел
Решение: При подстановке вместо переменной х бесконечности (
 , т.к. величины
, т.к. величины III. Вычисление первого и второго замечательного предела
Первый замечательный предел
Свойства:
Второй замечательный предел
 | |
Пример 3. Вычислить предел
Решение: При подстановке вместо переменной х числа 0 видим, что получается неопределенность вида
Задания для самостоятельной работы:
| I вариант | II вариант | III вариант |
| «3» | ||
| а) | а) | а) |
| б) | б) | б) |
| в) | в) | в) |
| г) | г) | г) |
| «4-5» | ||
| а)  | а) | а) |
| б) | б) | б) |
| в) | в)  | в) |
| г) | г) | г) |
«Предел функции в точке и на бесконечности. Вычисление пределов»
Вариант 1.
1.Найдите пределы последовательностей:
-
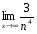 ; 3)
; 3) 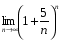 ;
; -
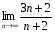 ; 4)
; 4) 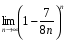 .
.
2.Найдите пределы функций:
-
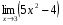 ;
; -
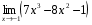 ;
; -
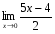 ;
; -
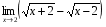 ;
; -
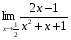 .
.
3. Раскрытие неопределенностей вида
-
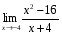 ; 3)
; 3) 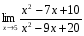 ;
;
2)
4. Раскрытие неопределенностей вида
1)
Раздел 2 Дифференциальное исчисление
Тема 2.1 Производная функции.
Практическое занятие №2 Нахождение производных функции. Нахождение производной сложных функций.
Цель работы:
Проверить умения нахождения производной функции.
