ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

М.ӘУЕЗОВ АТЫНДАҒЫ ОҚМУ КОЛЛЕДЖІ

«Келісілді» М.Әуезов атындағы ОҚМУ колледжінің әдіскері Еспенбетова Ш.А. ________________ « ___ » _____ 2019ж.

«Бекітемін» М.Әуезов атындағы ОҚМУ колледж директорының оқу ісі жөніндегі орынбасары ________________ « ___ » _____ 2019 ж.

Ашық сабақ жоспары

Тақырыбы: «Цилиндр, конус және қиық конус»


Пән: «Математика»

Топ: ВЕТн-18-15К

Оқытушы: Оралова М.Ә.

Мерзімі: 08.04.2019 жыл

Дәрісхана: 218

Уақыты: 10.10-11.40


Шымкент 2019 ж.

Ашық сабақ жоспары №
Пән:«Математика»

Тобы	ВЕТн-18-15К
Күні	08.04.2019

Оқытудың түрі және жүйесі: Жаңа білімді меңгеру сабағы.

Сабақтың типі: Дәріс сабағы.

Сабақтың тақырыбы: Цилиндр, конус және қиық конус.

Сабақтың мақсаттары:

Білімділік: Цилиндр, конус, қиық конус анықтамаларын бекіту, құрылымын анықтау, бүйір беттерінің,толық беттерінің формулаларын есеп шығаруда қолдана білу.

Дамытушылық: Ойлау қабілетін дамыту, математикалық тіл байлығын арттыру, оқу дағдыларын қалыптастыру. Өздігінен білім алып, дами алатын жеке тұлғаны қалыптастыру.

Тәрбиелік: Өз бетімен жұмыс, топпен жұмыс жасауға тәрбиелеу, алдына қойған мақсатына табандылықпен жетуге тәрбиелеу.

Сабақтың түрі: жаңа тақырыпты игеру сабағы (аралас әдісті).

Пәнаралық байланыс: математика, химия, физика, геометрия.

Оқытудың әдістері және ынталандыру: «Атом-молекула» әдісі, «Kahoot» ойын әдісі, «Әріптерді сөйлетейік» әдісі, «Құбыр салу» әдісі.

---

Сабақтың әдістемелік қамтамасыз етілуі: оқулықтар, геометриялық модельдер, үлестірмелі қағаздар, тест парақшалары, бағалау парағы, оқулық жұмыс дәптері, логикалық тапсырмалар, телефон интернетке қосылған т.б.

Әдебиеттер:

Негізгі әдебиеттер:

1. 
   А.Е.Әбілқасымова, З.А.Жұмағұлова, А.Абдиев, В.Е.Корчевский. Алгебра және анализ бастамалары. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-шы сыныбына арналған оқулық. Алматы: Мектеп, 2015
   
2. 
   И.Бекбоев, В.Гусев, Ж.Қайдасов, А.Абдиев. Геометрия. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-шы сыныбына арналған оқулық. Алматы: Мектеп, 2014
   
3. 
   В.Гусев, Ж.Қайдасов, Ә.Қағазбаева. Геометрия. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 10-шы сыныбына арналған оқулық. Алматы: Мектеп, 2015
   

Қосымша әдебиеттер:

1. 
   И.П.Рюстюмова, С.Т.Рюстюмова Тренажер по математике для подготовки к ЕНТ. Алматы: 2011
   
2. 
   Ғ.Суханбердина. Геометрия пәнінен тестер жинағы (математика мамандығы) Астана: Фолинат, 2012
   

 Оқу құралдары мен электронды оқулықтар тізімі:

 Web-resources:

1. 
   http://www. kz@gmail.com.
   
2. 
   http://bilimdiler.kz/
   
3. 
   ©www.melimde.com 2017
   

Сабақтың құрылымы мен мазмұны

Сабақтың кезеңдері	Сабақтың кезеңдерінің мазмұны мен сұрақтары	Уақыт (минут)
I.Ұйымдастыру кезеңі	Сәлемдесу, түгелдеу, аудиторияның тазалығына мән беру, студенттердің зейінін сабаққа аудару.	3
II.Сабақтың мақсатын және жұмыс жоспарын хабарлау	«Атом-молекула» әдісін қолданып, жаңа сабақтың тақырыбы мен мақсатына тоқталу. Мақсатқа жету жолын айқындау.	7
III.Студенттердің білімін бақылау. Үй тапсырмасын тексеру.	Үй тапсырмасын «Kahoot» ойын әдісін қолдана отырып, білімгерлерге 20 сұрақ беру арқылы үй тапсырмасына дайындықтарын анықтау. «Kahoot» ойыны интернет желісі арқылы ойнатылады. Онда 20 сұрақтың әрқайсысына 20 секунттан беріледі. Ойын соңында әрбір қатысушы жеке ұпайлар жинақтайды. Ойынның мақсаты білімгерлерді жылдамдыққа үйрету.	15
IY.Түсіндіре отырып баға қою.	Белсенділік танытып, қосымша тапсырмаларға дайындалған білімгерлерді ынталандыру мақсатында бағалау.	5
Y. Жаңа тақырыпты хабарлау және оның жоспарымен таныстыру.	Сабақтың мақсаты: Цилиндр, конус, қиық конус анықтамаларын бекіту, құрылымын анықтау, бүйір беттерінің, толық беттерінің формулаларын есеп шығаруда қолдана білу. 1. Цилиндр, конус, қиық конус ұғымдарына түсінік беру. 2. Цилиндр, конус, қиық конустың ауданын және көлемін есепеу. 3. Цилиндр, конус, және қиық конусқа берілген есептерді шығару.	5
YI. Жаңа тақырыпты түсіндіру	Жаңа тақырыпты оқулыққа сүйене отырып, тақтада түсіндіру: Цилиндр (көне грекше: κύλινδρος — білік, цилиндр) цилиндр немесе цилиндрлік бет — берілген бағытқа параллель және бағыттауыш сызық арқылы өтетін кеңістіктің жасаушы түзулерінің жиыны; тұйық цилиндрлік бетпен және өзара параллель екі жазықтықпен (Цилиндр табандары) шектелген дене . Егер Цилиндрдің табандары оның жасаушыларына перпендикуляр болса, онда ол тік Цилиндр деп аталады. Табандары дөңгелек болып келген тік Цилиндрді тік дөңгелек Цилиндр не дөңгелек Цилиндр деп атайды . Мұндай Цилиндрдің көлемі V=πr2h-қа, ал бүйір беті S=2πrh-қа тең. 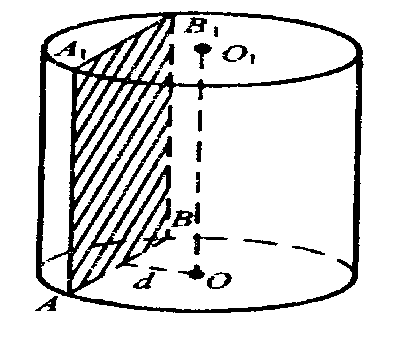Конус (лат. conus, гр. ‘konos’ ) Конус немесе конустық бет–белгілі бір сызықтың (бағыттаушы) барлық нүктесін кеңістіктің берілген нүктесімен (төбесімен) қосатын түзулердің (жасаушыларының) геометриялық орны. Егер бағыттаушы түзу сызық болса, онда конус жазықтыққа айналады. Егер бағыттаушы өзінің төбесімен бір жазықтықта жатпайтын 2-ретті қисық сызық болса, онда 2-ретті Конус шығады. Дөңгелек конус немесе тік дөңгелек конус 2-ретті конустың қарапайым түрі, оның бағыттаушысы шеңбер болады, ал төбесі осы шеңбер центріне ортогональ проекцияланады. Элементар геометрияда дөңгелек конус деп бағытталған шеңбері бар, дөңгелек конустың бетімен және оның осіне перпендикуляр жазықтықпен шектелген геометриялық денені айтады. Қиық конус — конустың табаны мен осы табанға параллел жазықтықпенқиылып шектелген бөлігі. Басқаша айтқанда толық конустың сүйір ұшы қырқылып тасталған «мұқыл» конус. Тарихқа үңілсек Конус гректің «konos» сөзінен аударылғанда « шыршаның дәні » дегенді білдіреді. Адамдар конуспен баяғы заманнан бері таныс. 1906 жылы Архимедтің (287–212 гг. до б.з.д.) «Әдіс туралы» кітабында, цилиндрлардың қиылысқан көлемдерін табу ережелері жазылған. Бұл еңбекті пайдаланып екі ғсырдан кейін Демокрит пирамида мен конустың көлемдерінің формулаларын тапқан.	15
YII. Өткен білімдерге сүйене отырып, оқу әрекетін дамыту.	Өткен тақырып бойынша білімгерлердің білімдерін бақылау мақсатында «Әріптерді сөйлетейік» (латын әріптерін біріктіріп формула құрастыру) әдісін қолдану. Құрастырылған формулаларды қолданып, есептер шығарамыз. Топпен жұмыс: І топ. Цилиндрдің осьтік қимасының диоганалы 26 см-ге, биіктігі 24 см-ге тең. Цилиндрдің бүйір бетінің ауданын табыңдар? ІІ топ. Цилиндрдің осьтік қимасының ауданы 120 см2 , биіктігі 15 см-ге тең. Цилиндрдің толық бетінің ауданын табыңдар? ІІІ топ. Цилиндрдің осьтік қимасының ауданы 24 см2 , биіктігі 15 см-ге тең. Цилиндрдің бүйір бетінің ауданын табыңдар? Тақтамен жұмыс (жеке оқушыларға): 1) Цилиндр табанының диаметрі 1 м, ал биіктігі табанындағы шеңбердің ұзындығына тең. Цилиндрдің бүйір бетінің ауданын табыңдар? 2) Биіктігі 30 см, табанының диаметрі 20 см болатын цилиндр тәрізді шелек жасау үшін қанша метр квадрат қаңылтыр керек? Жаңа тақырыпты пысықтау мақсатында «Басқыш» тапсырмалары (топтық жұмыс) әдісін қолданамыз. «Басқыш» тапсырмалары әдісінде тақырыпқа қатысты есептер болады, сол есептерді баспалдақ көтерілген сайын жай есептерден күрделі есептерге көшеміз. Қабырғалары 6 см және 10 см тіктөртбұрышты кіші қабырғасынан айналдырғанда пайда болатын дене бетінің ауданын табыңдар. Цилиндрдің биіктігі 10 см. Осьтік қимасының ауданы 84 см2. Цилиндр табанының ауданын табыңдар. Цилиндр табанының ұзындығы 8 см, ал осьтік қимасының диоганалі 17 см. Цилиндрдің жасаушасын табыңдар. Цилиндрдің толық бетінің және бүйір бетінің аудандары сәйкесінше 50 см2және 30 см2. Цилиндрдің радиусын және биіктігін табыңдар. Цилиндрдің биіктігі оның радиусынан 12 см артық, ал толық бетінің ауданы 288 см2. Цилиндрдің радиусы мен биіктігін табыңдар? Жауаптары: №1 Жауабы: Sт.б= 320 см2 № 2 Жауабы: Sтаб= 17,61 см2 №3 Жауабы: H = 15 см №4 Жауабы: R=  см , H = 1,5  см №5 Жауабы: R= 6 см, H = 18 см	20
YIII. Жаңа тақырыпты бекіту	Жаңа тақырыпты бекіту мақсатында «Kahoot» ойын әдісін қолданылады. Білімгерлерге 10 сұрақ беру арқылы жаңа тақырыпты қалай меңгергенін анықтау. «Kahoot» ойыны интернет желісі арқылы ойнатылады. Онда 10 сұрақтың әрқайсысына 20-30 секунттан беріледі. Ойын соңында әрбір қатысушы жеке ұпайлар жинақтайды.	10
IX. Сабақты қорытындылау	Сабақты қорытындылау үшін «Құбыр салу» әдісін қолдану. Барлық білімгерлер таратылған парақшаларға жаңа тақырыпта білген ілімін жазады. Парақшаларды құбыр тәрізді ыстық алақандарымен біріктіріп, құбырдың басынан кіші өлшемді доп жібереді. Доп парақшадан парақшаға ауысқанда білімгерлер түйін сөз айтады. Доп түйін сөздердің барлығын жинап өтеді. Доп құбырдың соңына жеткенде мақсатымызға жеткендігіміз айқындалады. Сабақ барысындағы белсенділігіне қарай білімгерлерді бағалау.	5
X.Үйге тапсырма беру:	А.Е.Абылкасымова, К.Д.Шойынбеков. Алгебра және анализ бастамалары. Жалпы білім беретін мектептің жаратылыстану-математика бағытындағы 11-шы сыныбына арналған оқулық. Алматы: Мектеп, 2011. ІІ тарау §5,6,7 оқу. 51-52 беттен № 22-27 есептерін шығару.	5

---

Оқытушы: ___________ Оралова М.Ә.

ПЦК төрайымы: _________ Алменова Ф.Б.

Тақырып: Цилиндр, Конус және қиық конус.

Негізгі мақсаты:  Цилиндр, конус, қиық конус анықтамаларын бекіту, құрылымын анықтау, бүйір беттерінің,толық беттерінің формулаларын есеп шығаруда қолдана білу.

Негізгі түсініктер: Цилиндр, конус және қиық конус, аудан, биіктік, радиус, диаметр, толық бетінің ауданы.

Жоспар:

Сабақтың мақсаты:

1. Цилиндр, конус, қиық конус ұғымдарына түсінік беру.
2. Цилиндр, конус, қиық конустың ауданын және көлемін есепеу.

3. Цилиндр, конус, және қиық конусқа берілген есептерді шығару.
Цилиндр- айналу денесі

«Цилиндр» сөзі гректің kulindros сөзінен алынған, ол «валик» - «оқтау» мағынасын білдіреді.

Aнықтама. Цилиндр деп тіктөртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын фигураны (денені) атайды.

Бізді қоршаған ортада, тұрмыста цилиндр пішіндес заттар, обьектілер жиі кездеседі: металдан жасалған бөшкелер, консерві банкалары, хоккейдің шайбасы және т.б.

Төмендегі суретте АОО1В тіктөртбұрышын оның ОО1 қабырғасын қамтитын l осінен айналдырғанда шыққан цилинд бейнеленген.

ААО1В тіктөртбұрышының ОО1 осіне параллель АВ қабырғасы цилиндрдің бүйір беті деп аталатын қисық бетті жасайды және ол цилиндрдің жасаушысы деп аталады. АО және О1В кесінділерінің айналуынан цилидірдің табандары деп аталатын өзара тең екі дөңгелек аламыз. Сонымен цилиндрдің беті цилиндрдің табаңдары деп аталатын екі дөңгелектен және цилиндрдің бүйір бетінен тұрады.

Егер цилиндрдің жасаушысы оның табанына перпендикуляр, яғни цилиндрдің биіктігіне тең болса, онда цилиндр тік дөңгелек цилиндр деп аталады.

Цилиндрдің қимасы

Цилиндрдің жазықтықпен қимасы деп жалғыз нүктеден, цилиндрдің жасаушысынан немесе табанынан өзгеше фигураны, яғни аталғандардан өзге цилиндр мен жазықтықтың ортақ бөлігін атайды.

1. 
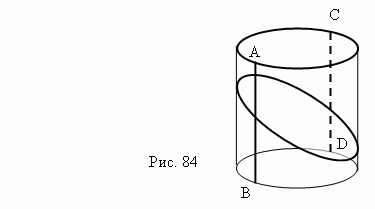
   Қиманы цилиндрдің осі арқылы жүргізуге болады. Мұндай қималар осьтік қималар деп аталады. Егер цилиндрдің остік қимасы квадрат болса, ондай цилиндр теңқабырғалы деп аталады.
   

---

2. 
   Қиманы цилиндрдің осіне жүргізуге болады. Бұл қима цилиндр мен екі жасаушыдан өтетін жазықтықтың қиылысуынан алынып тұр.
   
3. 
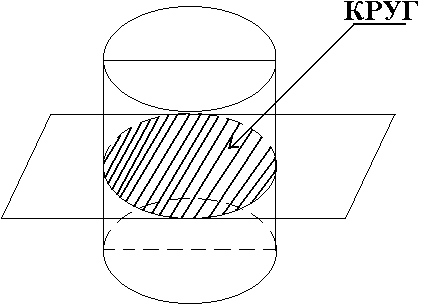
   Цилиндрді оның осіне перпендикуляр жазықтықпен қиюға да болады.
   
4. 
   Егер цилидрдің бүйір бетін оның табандарын қимайтын және цилиндр осіне перпендикуляр емес «в» жазықтықпен қисақ, онда қимада элипс аламыз.
   

Теорема: Цилиндрдің бүйір бетінің ауданы табан шеңберінің ұзындығын оның биіктігіне көбейткенге тең, яғни

S _ц.б.б = 2π RH

S _ц.т.б = 2 π RH+2 R²

S _ц.т.б = 2 πR(H+R)

Конус. Айналу денесі- конус.

Анықтама: Тікбұрышты үшбұрышты катетінен айналдырғанда шығатын фигура конус деп аталады. Грек. Ronos- «қарағай бүршігі»

Анықтама: Конустың төбесінен оның табан жазықтығына жүргізілген перпендикуляр конустың биіктігі болады. Табан шеңберінің кез келген нүктесін конустың төбесімен қосатын кесінділердің проекциялары тең, сондықтан олар – тең кесінділер. Бұл кесінділер конустың жасаушылары деп аталады. Конустың бүйір беті де конустық бет деп аталады.

Конус табанының

---

радиусы R жасаушысының ұзындығы l ал биіктігі H болсын. Пифагор теоремасына сәйкес бұл шамалар l ²= R² +H²

Теорема: Конустың бүйір бетінің ауданы оның табан шеңберінің ұзындығы мен жасаушының көбейтіндісінің жартысына тең, яғни

S = πRl

R- конус табанының радиусы, l-конустың жасаушысы.

S = πRl+πR² = πR(l+R),

R- табанының радиусы, l-конустың жасаушысы.

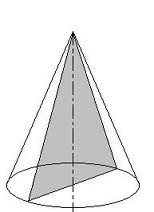
Конустың қимасы.

1. 
   Конустың қайсыбір екі жасаушысын қамтитын екі түзу арқылы бір ғана жазықтығын жүргізуге болады. Бұл жазықтық конустың табанын хорда бойымен, ал бүйір бетін екі жасаушы боймен қиып өтеді.
   
2. 
   Аталған жазықтық пен конустың ортақ бөлігі теңбүйірлі үшбұрыш болып табылады.
   
3. 
   Егер α жазықтығы конустың осі арқылы өтсе, онда қимада пайда болған үшбұрыш конустың осьтік қимасы деп аталады.
   
4. 
   Егер конустың бүйір бетін табанымен қиылыспайтын және конустың осіне перпендикуляр емес жазықтықпен қиып өтсек, онда қимада элиппс аламыз.
   

Анықтама: Конустың табаны мен табанына параллель қиманың арасындағы бөлігі қиық конус деп аталады.

Анықтама: қиық конустың бір табанының қайсыбір нүктесінен екінші табан жазықтығына түсірілген перпендикуляр қиық конустың биіктігі деп аталады.

Конустың бүір бетінің ауданының формуласы бойынша

S_{қ.кон.б.б.} = πl(R+r)

Теорема: Қиық конустың бүйір бетінің ауданы табан шеңберлерінің қосындысының жартысы мен жасаушының көбейтіндісіне тең

---

Смотрите также файлы

• Контрольная работа 2 Решите задачу. Функции внутреннего предложения и спроса условной страны на конкретный товар следующие.doc

• 1. азастан Республикасыны сырты саясатыны алыптасуы.docx

• Верещагин, И. К. Электролюминесценция кристаллов.pdf

• Вовк, А. А. Действие взрыва в грунтах.pdf

• Работы Индивидуальное задание вариант 76. Номер варианта по дисциплине Прикладная физика в электроэнергетике Наименование учебной дисциплины.docx