Задана схема на рис. 1,а. Параметры элементов:

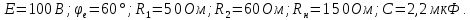
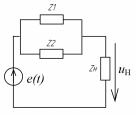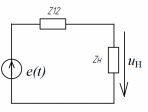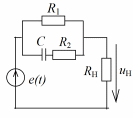
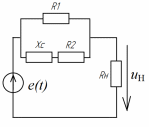
Рис. 1. Схема цепи для примера: исходная (а); комплексная (б); после параллельного преобразования (в) и последовательного (г) соединения элементов

Построение комплексной схемы замещения цепи. Для этого в исходной схеме все элементы заменим соответствующими схемами замещения (рис. 2.1,б). Находим комплексное сопротивление конденсатора:





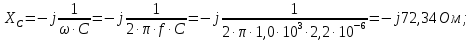
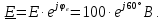
Нахождение комплексных действующих значений токов и
напряжений всех ветвей цепи. Преобразуем последовательное
соединение сопротивлений и 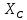на рис. 2.1,б к
эквивалентным сопротивлениям на рис. 2.1,в:







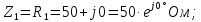
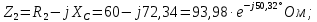
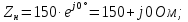
Параллельное соединение сопротивлени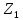й и 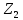на рис. 2.1,б
преобразуем к эквивалентному сопротивлению 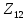на рис. 2.1,в: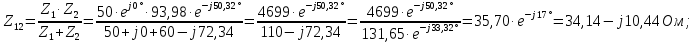



Последовательное соединение сопротивлени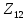й и 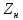на рис. 2.1,в
преобразуем к эквивалентному сопротивлению

---

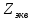
на рис. 2.1,г:



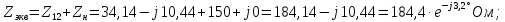
Из схемы на рис. 2.1,г находим по закону Ома комплексный
действующий ток:



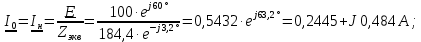
Из этой же схемы на рис. 2.1,г находим комплексное
действующее напряжение:



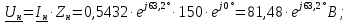
Находим комплексное действующее напряжение на нагрузке :



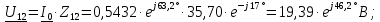
По схеме на рис. 2.1,в находим комплексные действующие токи
сопротивлений и :





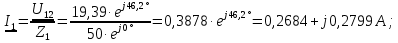
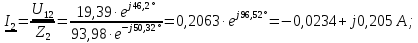
Проверяем выполнение закона Кирхгофа для токов:



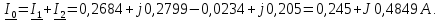
Как видно, погрешность результата наблюдается в третьем знаке,
что соответствует числу используемых разрядов.

Находим комплексные действующие значения напряжений:









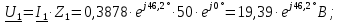
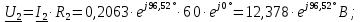
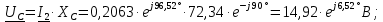
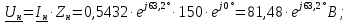
Нахождение комплексных амплитудных значений токов и
напряжений:

















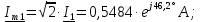
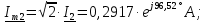
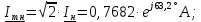
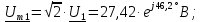
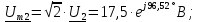
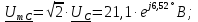
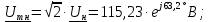
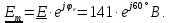
Расчет активной и реактивной мощности всех элементов цепи
Комплексная, активная и реактивная мощности источника ЭДС:

---

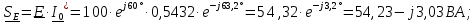
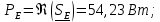
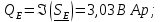
Активная мощность резисторов:









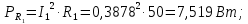
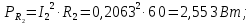
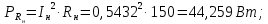
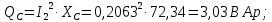
Проверка баланса активной и реактивной мощности в цепи
Сумма активных мощностей резисторов:



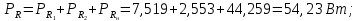
Сумма реактивных мощностей конденсатора:



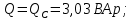
Активная и реактивная мощности источника равны
соответствующим мощностям потребителей с погрешностью 1%.

Формулы для мгновенных значений входной 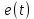и выходной
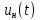функции. Формулы записываются по соответствующим
комплексным значениям:





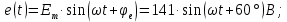
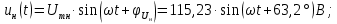
Построение графиков входной и выходной функций:

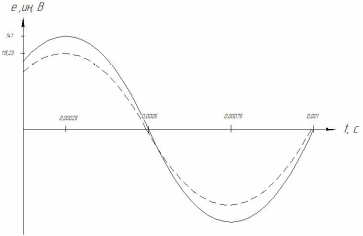Рис. 2. Графики функци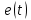й (−) и (--)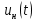

По кривым на рис. 2 можно сделать вывод, что напряжение на
нагрузке 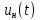опережает по фазе входное напряжения .

---

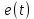Смотрите также файлы

• 1. Кратко расскажите о проблемах экономики в ссср в 1950е 1980е гг.docx

• Обучающийся Елизарова Сабрина Александровна Преподаватель Никифорова Татьяна Евгеньевна Практическое занятие.rtf

• Аддиктивное поведение в художественной литературе по произведениям М. Булгакова Морфий иФ. Достоевского Игрок.doc

• Чекмарев, А. П. Гнутые профили проката.pdf

• Червякова, В. В. Сложные латуни и бронзы. Свойства, строение и вопросы технологии.pdf