ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема урока: «Решение показательных уравнений»
Тип урока: урок обобщения, систематизации знаний.
Цели урока:
Образовательные:
-
Обобщить и структурировать знания учащихся по данной теме. -
Закрепить основные методы решения показательных уравнений, предупредить появление типичных ошибок. -
Предоставить каждому обучающемуся возможность проверить свои знания и повысить их уровень. -
Активизировать работу класса через разнообразные формы работы.
Развивающие:
-
Работать над развитием понятийного аппарата; -
Развивать навыки самоконтроля.
Воспитательные:
-
Воспитывать ответственное отношение к труду; -
Воспитывать волю и настойчивость для достижения конечных результатов.
ФОРМА УРОКА: комбинированный.
Оборудование. Доска, мел, карточки с тестовыми заданиями, мультимедийный проектор, презентация (Приложение 1).
Ход урока
I.Орг. момент.
Здравствуйте, ребята!
На доске написана китайская мудрость:
Девиз урока
РАССКАЖИ МНЕ –И Я ЗАБУДУ ,
ПОКАЖИ МНЕ –И Я ЗАПОМНЮ ,
ДАЙ МНЕ ДЕЙСТВОВАТЬ – И Я ПОЙМУ.(слайд 1)
Сегодня на уроке мы с вами повторим основные методы решения показательных уравнений, выполним самостоятельную работу по данной теме.(слайд 2)
Цели урока:
1Обобщить знания учащихся по данной теме.
2.Закрепить основные методы решения показательных уравнений, предупредить появление типичных ошибок.
3.Предоставить каждому обучающемуся возможность проверить свои знания и повысить их уровень.
II. Систематизация теоретического материала .
Актуализация опорных знаний
(обобщение материала провести фронтально с классом)
-
Дать определение показательной функции.(слайд 3) -
Перечислить свойства показательной функции.(слайд 4) -
Перечислить свойства степеней. .(слайд 5) -
Дать определение показательного уравнения.(слайд 6)
Давайте вспомним основные методы решения показательных уравнений. Сконцентрируйте внимание на изображении, созданном медиапроектором. (демонстрация слайда 7 презентации).
Первый из рассматриваемых нами способов решения уравнения – функционально-графический (демонстрация слайда 8 презентации).
Давайте вспомним алгоритм решения уравнений функционально – графическим методом.
Чтобы решить уравнение вида f(x)=g(x) функционально-графическим методом нужно:
-
Построить графики функций у=f(x) и y=g(x) в одной системе координат. -
Определить координаты точки пересечения графиков данных функций. -
Записать ответ.
Задание 1. Решите уравнение
. Ответ. 0. (В процессе решения уравнения демонстрируется слайд 9 презентации).Следующий метод решения уравнений – метод уравнивания показателей (демонстрация слайда 10 презентации).
Задание 2. Решите уравнения, комментируя свое решение. (В процессе решения уравнения демонстрируется слайд 11 презентации)
, 
, х2-4х=-3, х2-4х+3=0, х1=1, х2=3.Следующий метод решения уравнений – введение новой переменной (демонстрация слайда 12 презентации).
Задание 3.Решите уравнения, комментируя свое решение. (В процессе решения уравнения демонстрируется слайд 13 презентации)
,
,
.Пусть 3х=, t>0, тогда t2-24t-81=0, t1=27, t2=-3.
Выполним обратную замену.
| 3х=27, | 2) 3х=-3, |
| х=3. | решений нет. |
Следующий метод решения уравнений – Разложение на множители (демонстрация слайда 14 презентации).
Задание 4.Решите уравнения, комментируя свое решение. (В процессе решения уравнения демонстрируется слайд 15 презентации).
;
;
;
;
;
; 5х=3, х=0,6.Указать методы решения следующих уравнений: слайд 16
42-2х+1=48
2х=3
7
х-6 * 7х+5=02 х+2=4
ВОПРОС : О ЧЁМ ИДЁТ РЕЧЬ.? слайд 17
-
? ОСОБЕННОЕ !
1).3х = 27
2). 6х-3 = 36
3). 5х-2 =25
4). 2х = 32 + а
ОТВЕТ : 1, 2, 3 –простейшие показательные уравнения 4 –простейшее показательное уравнение с параметром а ,при а=0 имеет решение.
Цитата дня: «Учение без размышления бесполезно, но и размышление без учения опасно».
Конфуций. слайд 18
III. Тренинг
Итак, мы повторили все методы (известные нам ) решения показательных уравнений .А теперь закрепим эти методы при решении .
Предложить учащимся выполнить следующие задания, объединившись в микрогруппы для взаимопомощи и взаимоконтроля. Время выполнения - 5 минут.
По просьбе учащихся консультировать их по выполнению задания. слайд 19
| а) 3х+2 + 3х = 30 б) 4х – 14 . 2х – 32 = 0 | а) 2х+2 +2х = 5 б) 9х – 6 . 3х – 27 = 0 |
Во временных рабочих группах каждый может работать индивидуально .По выполнении каждого задания каждая группа помещает полученный ответ на доску. В случае получения различных ответов, рассматривается верный способ решения.
1 вариант-а)1; б)4.
2 вариант-а)0; б)2.
Показать границы применения полученных знаний при выполнении заданий КИМ
Познакомить учащихся с формулировкой заданий ЕГЭ прошлых лет, требующих для решения знания изученного материала. Предложить по желанию одному из учащихся показать решение каждого задания с комментариями.
По одному решают задания у доски, остальные – записывают решение в тетрадь, участвуют в выборе способа решения, в обсуждении хода решения.
Решение задач высокого уровня сложности (часть С) (Решение у доски с комментированием)
а) Решить уравнение:
б) При каких значениях параметра p уравнение имеет единственное решение:
Ответы
а) Решить уравнение:
Решение:
Пусть t=
. Тогда t>0.
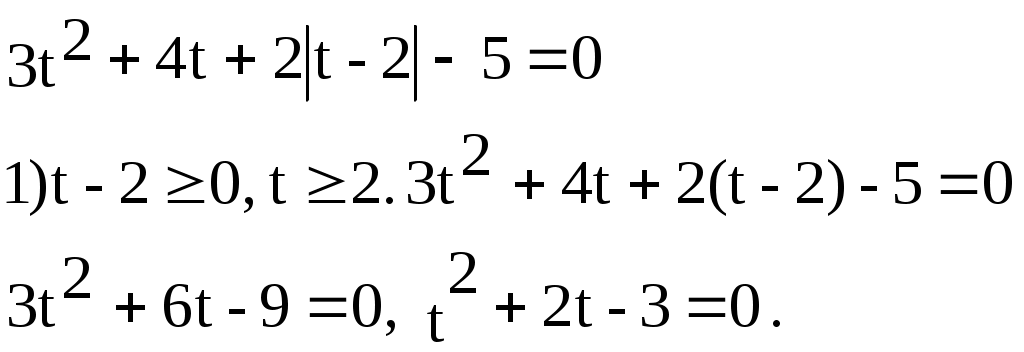
По теореме, обратной теореме Виета, t1=-3, t2=1.
Найденные значения t не удовлетворяют условию рассматриваемого случая
2) 0 < t < 2.
. t2=-1 не удовлетворяет условию рассматриваемого случая 0 < t < 2.
. Так как функция монотонна, то x = - 1 Ответ: x = - 1.
б) При каких значениях параметра p уравнение имеет единственное решение:
(1)Решение:
Пусть
тогда уравнение примет вид 
(2)
Уравнение (1) имеет единственное решение, если уравнение (2) имеет один положительный корень. Это возможно в следующих случаях:
-
Если D = 0, то есть p = 1, следовательно, уравнение (1) имеет единственное решение x = 0. -
Если p ≠ 1, то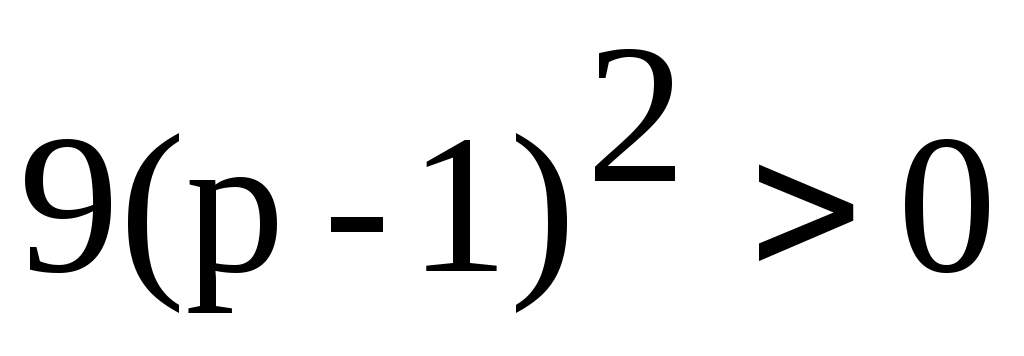
, тогда уравнение (2) имеет два различных корня 
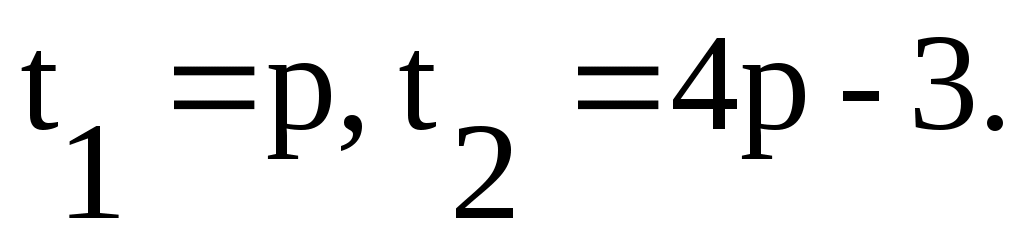Условию задачи удовлетворяет совокупность систем 
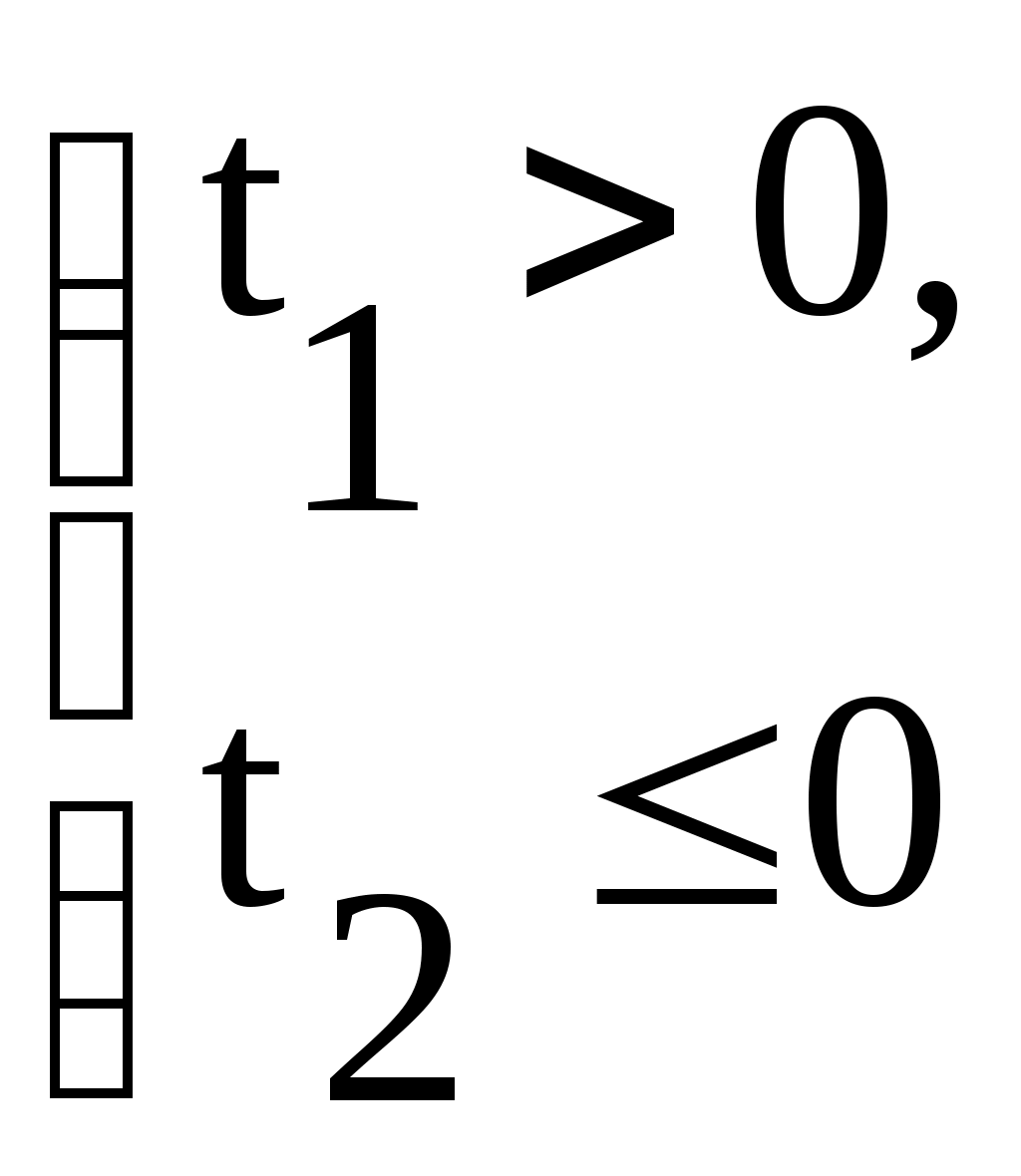или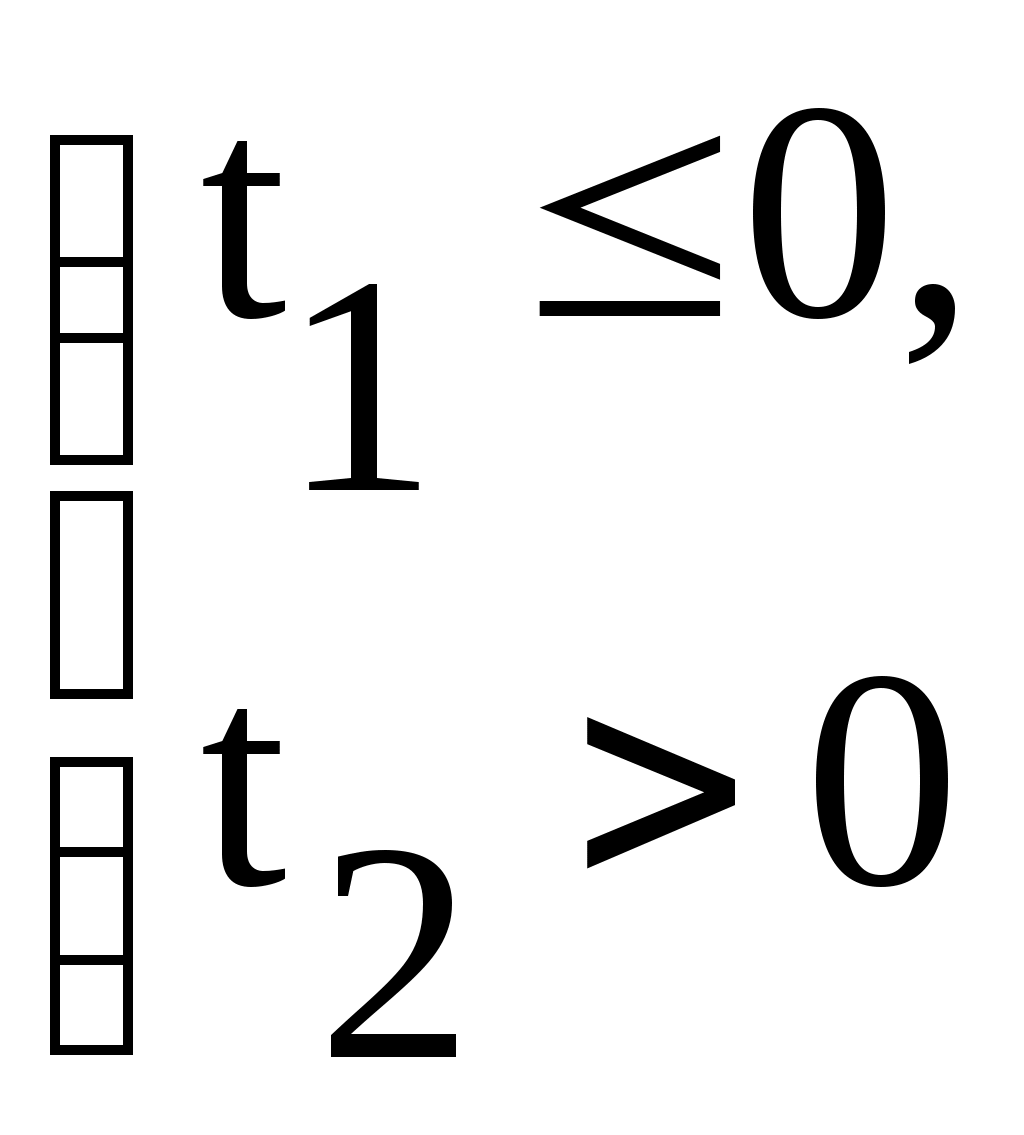 
Подставляя t1 и t2 в системы, имеем
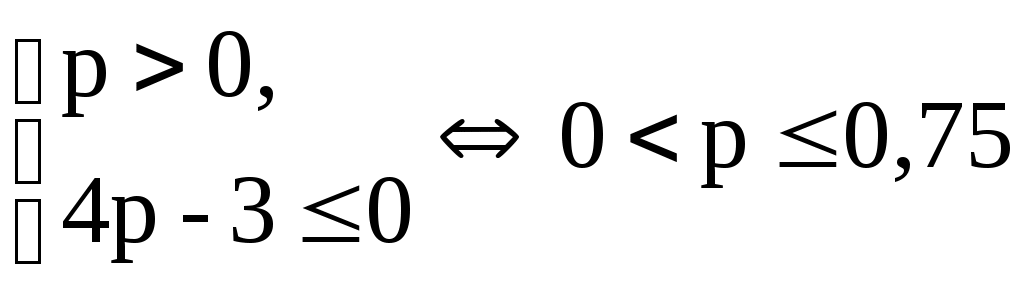
или
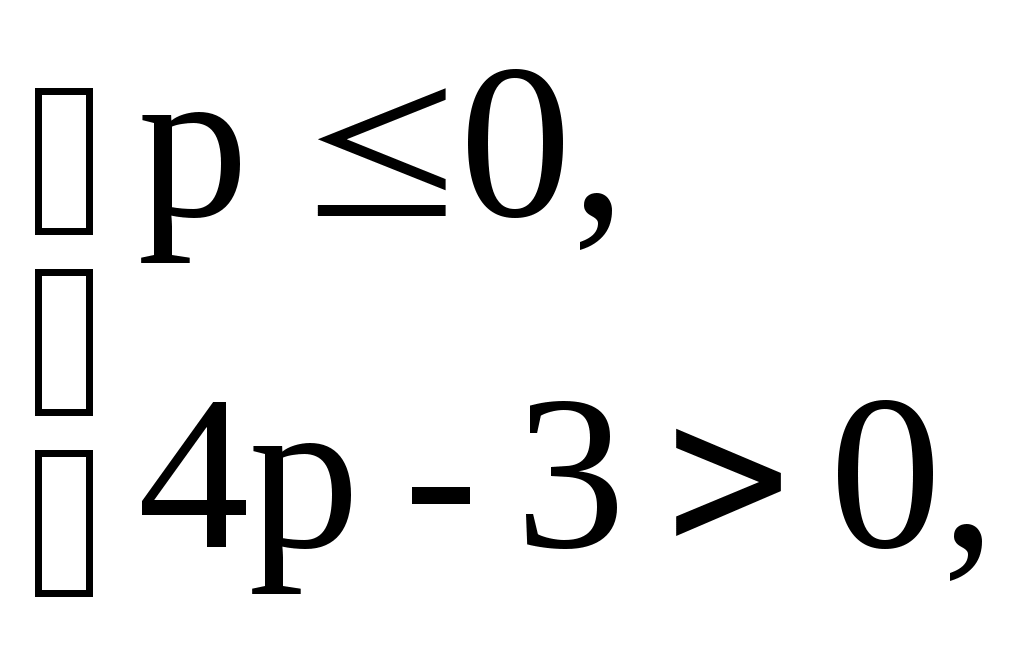нет решений.Ответ: p = 1, 0 < p ≤ 0,75.
«Спорьте,
заблуждайтесь,
ошибайтесь,
но, ради Бога, размышляйте,
и, хотя криво – да сами».
Г. Лессинг.
слайд 20
ФИЗМИНУТКА
А сейчас мы с вами проведем физкультминутку. слайд 21
Проводится гимнастика для улучшения мозгового кровообращения.
Исходное положение – сидя на стуле, руки на пояс.
Упражнение №1.Голову наклонить вправо. И. п. Голову наклонить влево. И. п. (Упражнение повторяется 6 раз).
Упражнение №2. Голову повернуть направо. И.п. Голову повернуть налево. И. п. (Упражнение повторяется 6 раз).
Упражнение №3. Правая рука – вперёд, левая – вверх. И. п. Левая рука – вперёд, правая – вверх. И. п. (Упражнение повторяется 6 раз).
Упражнение №4. И.п. – откинувшись на спинку стула.
Работаем по офтальмотренажеру.
По 4 раза, не поворачивая головы, глазами проводим вверх – вниз, затем влево – вправо,
4 раза по часовой стрелке по наружному овалу,
4 раза против часовой стрелки по внутреннему овалу,
и 4 раза рисуем глазами знак бесконечности.
IV.Тестовая работа.
А сейчас проведем тестовую работу, чтобы выяснить как вы усвоили данную тему и какие пробелы у вас остались. Задания раздаются каждому ученику, решение каждого здания учащиеся выполняют письменно и сдают вместе с бланком ответов.(Приложение 2)