Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное

Учреждение высшего профессионального образования

«Магнитогорский государственный технический университет им. Г.И. Носова»

Кафедра физической химии и химической технологии

РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

По курсу «Физическая химия»

Раздел «Термодинамический анализ химических реакций»

Вариант 1.5

Выполнила: Мухина В.В.

Студент группы: МХб-20-1

(подпись)

Проверил:

(подпись)

Магнитогорск

2021

Формулировка задания


Исследование 1



Для удобства последующих расчетов составляем таблицу исходных данных, используя справочный материал.
Таблица 1

Исходные данные для термодинамического расчета реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

Вещество	ΔНо298, кДж/моль	ΔSо298, Дж/мольК	Коэффициенты в уравнение а + bT+cT-2 , Дж/мольК
			a	b *10-3	c *10-5
Nb2O5	-1905,80	137,80	91,61	118,10	0
H2	0	130,60	27,28	3,26	0,50
NbO	-406,00	50,0	40,20	18,40	0
H2O	-241,84	188,74	30,0	10,71	0,33

1.1 . Расчет изменения изобарной теплоемкости ( 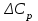) и теплового эффекта реакции ( )

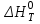Зависимость теплового эффекта реакции от температуры определяется законом Кирхгофа:

---

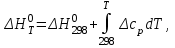(1)

где: 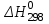– стандартный тепловой эффект реакции при 298 К;

- изменение теплоёмкости системы в результате протекания реакции.

Последняя величина рассчитывается по уравнению:

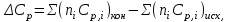(2)

где 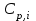- мольная изобарная теплоёмкость i-го вещества, определяемая из уравнения:

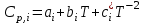(3)
Рассчитаем :
;

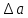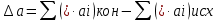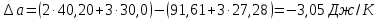Рассчитаем :

;

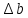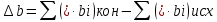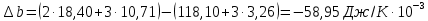
Рассчитаем



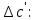
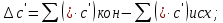
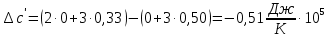
Найдем :
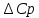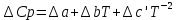
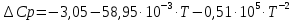Температурный интервал 1750-2000
с шагом: 50
При Т=1750:
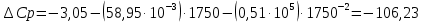Остальные 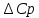при различных температурах рассчитывается аналогично.

Рассчитаем значения 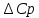при различных температурах и сведем эти значения в табл.2.


Таблица 2

T,K	1750	1800	1850	1900	1950	2000
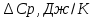	-106,23	-109,17	-112,12	-115,07	-118,01	-120,9

---

Зависимость изменения изобарной теплоемкости от температуры для реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)



По данным табл.2. построить зависимость .




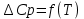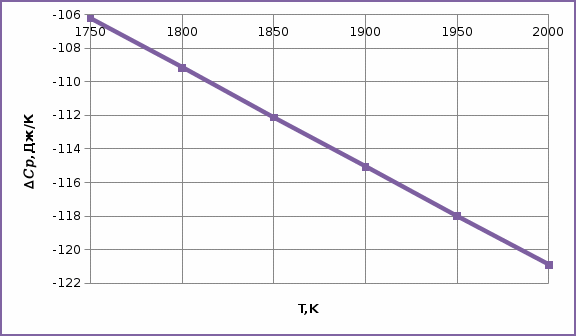
Рис.1. Зависимость изменения изобарной теплоемкости от температуры для реакции Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)
Значение _Н₂₉₈ в уравнении (1) определяется по стандартным теплотам образования _Н<sub>298, i

</sub>Н₂₉₈ = (n_i Н_{298, i} )_кон -  (n_i Н_{298, i})_исх. (4)

В рассматриваемом случае уравнение (4) имеет вид:

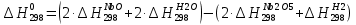(5)
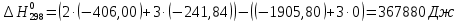В соответствии с заданием необходимо рассчитать тепловые эффекты в интервале температур 1750-2000К при шаге температуры 50К. Получим уравнение зависимости теплового эффекта реакции от температуры: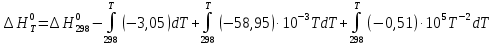








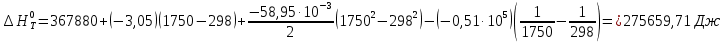
Остальные значения 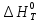при различных температурах T=1750-2000 рассчитываются аналогично.


Таблица 3

Величина 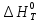при различных температурах для реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

T,K	1750	1800	1850	1900	1950	2000
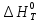, кДж	275659,71	2700274,59	264742,13	259062,3	253235,2	247260,75

Зависимость 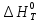=f(T), построенная по данным табл.3 представлена на рис.2.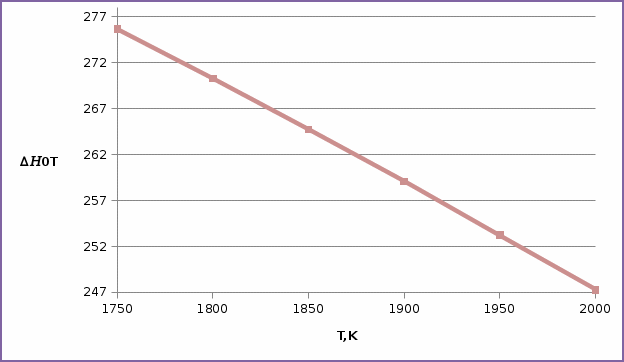




Рис.2. Зависимость теплового эффекта от температуры для реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

1.2Расчёт изменения энтропии реакции

---

Изменение энтропии системы в результате протекания процесса определяется по уравнению:

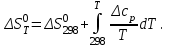(6)

В этом уравнении 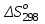– стандартное изменение энтропии для реакции при 298К, определяемое по мольным стандартным энтропиям веществ :

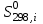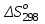= (n_i 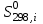)_кон - (n_i 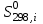)_исх (7)


Значения 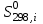для соответствующих веществ приведены в табл. 1, после их подстановки в уравнение (7) получим: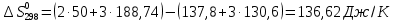



Выведем расчетное уравнение изменения энтропии от температуры:
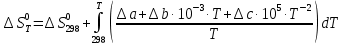
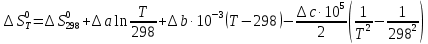, (8)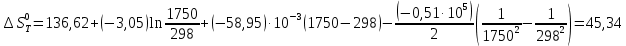
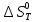Остальные значения при различных температурах T=1750-2000 рассчитываются аналогично.
Таблица 4

Значения изменения энтропии ( 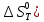при различных температурах для реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

T,K	1750	1800	1850	1900	1950	2000
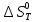, Дж/К	45,34	42,31	39,28	36,25	33,2	30,2

По данным табл.4 построим график .



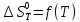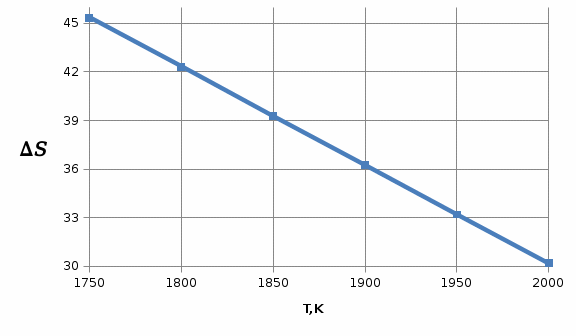
Рис.3. Зависимость изменения энтропии от температуры для реакции

---

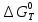
1.3. Расчет изменения стандартной энергии Гиббса

При расчете изменения стандартной энергии Гиббса для реакции воспользуемся уравнением Гиббса-Гельмгольца.
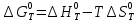, (9)
Найденные величины изменения стандартной энергии Гиббса приведены в табл.5, по данным которой построена зависимость 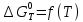_, изображенная на рис.4.

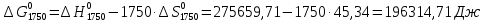Остальные значения при различных температурах T=1750-2000 рассчитываются аналогично.

Таблица 5

Значения изменения стандартной энергии Гиббса ( ) при различных температурах для реакции
Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

T,K	1750	1800	1850	1900	1950	2000
, кДж	196,31	194,11	192,07	190,18	188,49	186,86

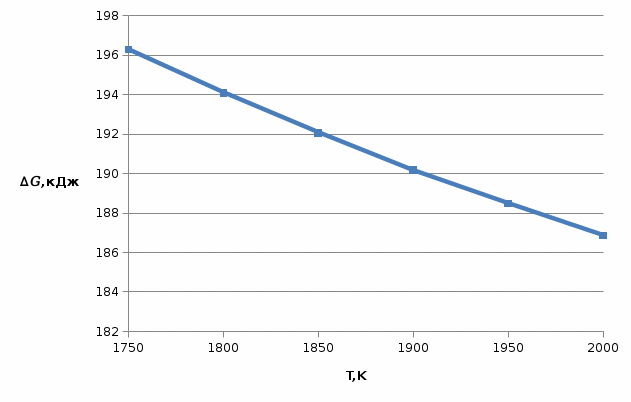
Рис.4. Зависимость изменения стандартной энергии Гиббса от температуры для реакции

Nb₂O_5(тв) + 3H_2(газ) = 2NbO + 3H₂O_(газ)

1.4. Вывод уравнения зависимости константы равновесия от температуры

Константа равновесия связана с изменением стандартной энергии Гиббса соотношением:

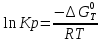(10)

После подстановки выражения (13) в уравнение (14) получим:


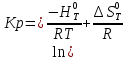(11)

Можно полагать, что в сравнительно небольшом интервале температур тепловой эффект реакции ( ) и изменение энтропии ( практически постоянные величины (это подтверждают и результаты табл.3 и 4). Отсюда уравнение можно записать в виде: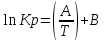

(12) ,

где A и B-постоянные, которые соответственно равны:

---

Смотрите также файлы

• Урок литературы в 9 классе Портрет Печорина Какие эпитеты использует автор Почему он использует уменьшительноласкательные суффиксы.ppt

• Вариант 1 1Прочитай. Найди ошибки. Запиши текст правильно.docx

• Решение кейса 4 Заключение 7 Список литературы 8 Условие Студентпрограммист Вас зовут Михаил, вам 18 лет.docx

• Дифференциация звуков СШ для детей 56 лет.docx

• Судимость и ее уголовноправовое значение.docx