Файл: Содержание Задание 1 Сравнительный анализ метода наименьших квадратов и метода макмального правдоподобия при определении параметров эконометрических моделей. Ответ.docx

Титульник
Содержание

Задание 1

Сравнительный анализ метода наименьших квадратов и метода макϲᴎмального правдоподобия при определении параметров эконометрических моделей.

Ответ

Задание 2

Данные каждого варианта определяется параметрами p1, p2. При выполнении контрольных заданий студент должен подставить там, где это необходимо, вместо буквенных параметров индивидуальные анкетные характеристики: p1 – число букв в полном имени студента (5 букв); p2– число букв в фамилии студента (9 букв).

Исследуется зависимость производительности труда 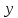(т/ч) от уровня механизации работ 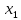(%), среднего возраста работников 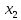(лет) и энерговооруженности 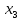(кВт/100 работающих) по данным 14 промышленных предприятий.

Таблица 1

№ завода	Уровень механизации работ,	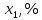Средний возраст работников,	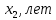Энерговооруженность,	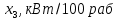Производительность труда,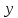
1	32+p1	33+p2	300+p2	20+p1
2	30+p1	31+p2	290+p1	24+p2
3	36+p1	41+p2	350+p2	28+p1
4	40+p1	39+p2	400+p1	30+p2
5	41+p1	46+p2	400+p2	31+p1
6	47+p1	43+p2	480+p1	33+p2
7	56+p1	34+p2	500+p2	34+p1
8	54+p1	38+p2	520+p1	37+p2
9	60+p1	42+p2	590+p2	38+p1
10	55+p1	35+p2	540+p1	40+p2
11	61+p1	39+p2	600+p2	4+p1
12	67+p1	44+p2	700+p1	43+p2
13	69+p1	40+p2	700+p2	45+p1
14	76+p1	41+p2	750+p1	48+p2
15	30+p1	32+p2	350+p2	25+p1
16	32+p1	31+p2	295+p1	24+p2
17	36+p1	45+p2	355+p2	30+p1
18	45+p1	35+p2	400+p1	32+p2
19	40+p1	48+p2	400+p2	35+p1
20	45+p1	40+p2	485+p1	33+p2
21	50+p1	35+p2	510+p2	32+p1
22	55+p1	48+p2	530+p1	35+p2
23	62+p1	52+p2	595+p2	40+p1
24	60+p1	35+p2	540+p1	42+p2
25	65+p1	39+p2	600+p2	47+p1

---

В соответствии с вариантом задания, используя статистический материал, необходимо выполнить:

1. Выбор факторов для регрессионного анализа:

1) корреляционный анализ данных, включая проверку теста Фаррара –Глоубера на мультиколлинеарность факторов;

2) пошаговый отбор факторов методом исключения из модели статистически незначимых переменных;

3) проверка теста на «длинную» и «короткую» регрессии (при несоответствии результатов, полученных в пунктах 1 и 2).

2. Построение модели множественной регрессии с выбранными факторами, экономический анализ коэффициентов уравнения.

3. Оценку качества модели регрессии:

1) проверка статистической значимости уравнения с помощью F-критерия Фишера;

2) проверка предпосылки МНК о гомоскедастичности остатков;

3) оценка уровня точности модели.

4. Построение доверительных интервалов для результирующей переменной и определение компаний с заниженным и завышенным фактическим уровнем энерговооруженности (производительности «у»). Ранжирование компаний по степени их эффективности на основе результатов моделирования.

5. Оценку степени влияния факторов на результат с помощью коэффициентов эластичност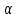и, и 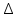коэффициентов. Выбор наиболее влияющего фактора.

6. Построение парной регрессии с наиболее влияющим фактором. Сравнение качества множественной и парной регрессий.

7. Прогнозирование энерговооруженности (производительности ) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения.

8. Графическое представление результатов моделирования.

Решение

В соответствии с исходными данными варианта составляем таблицу со значениями, которые необходимо обработать (таблица 2).

Таблица 2

Исходные данные

№ завода	Уровень механизации работ,	Средний возраст работников,	Энерговооруженность,	Производительность труда,
1	37	42	309	25
2	35	40	290	33
3	41	50	359	33
4	45	48	405	39
5	46	55	409	36
6	52	52	485	42
7	61	43	509	39
8	59	47	525	46
9	65	51	599	43
10	60	44	545	49
11	66	48	609	9
12	72	53	705	52
13	74	49	709	50
14	81	50	755	57
15	35	41	359	30
16	37	40	300	33
17	41	54	364	35
18	50	44	405	41
19	45	57	409	40
20	50	49	490	42
21	55	44	519	37
22	60	57	535	44
23	67	61	604	45
24	65	44	545	51
25	70	48	609	52

---

1. Выбор факторов для регрессионного анализа:

1) Корреляционный анализ данных, включая проверку теста Фаррара –Глоубера на мультиколлинеарность факторов.

На рис. 1 представлена матрица коэффициентов парной корреляции для всех переменных, участвующих в рассмотрении. Матрица получена с помощью инструмента Корреляция из пакета Анализ данных в MS Excel.

Матрица коэффициентов парной корреляции



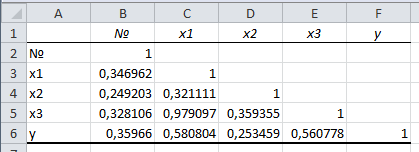
Рис. 1 – Матрица коэффициентов парной корреляции

Визуальный анализ матрицы на рис. 1 позволяет установить:

1) переменная имеет довольно высокие парные корреляции с переменными и . Переменную далее не будем рассматривать.

2) большинство переменных анализа демонстрируют довольно высокие парные корреляции, что обуславливает необходимость проверки факторов на наличие между ними мультиколлинеарности. Тем более, что одним из условий классической регрессионной модели является предположение о независимости объясняющих переменных.

Для выявления мультиколлинеарности факторов выполним тест Фаррара-Глоубера по факторам и .

Проверка теста Фаррара-Глоубера на мультиколлинеарность факторов включает несколько этапов, реализация которых представлена ниже.

Проверка наличия мультиколлинеарности всего массива переменных.

Построим матрицу межфакторных корреляций 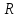(рис. 2) и найдем её определитель 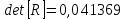с помощью функции МОПРЕД().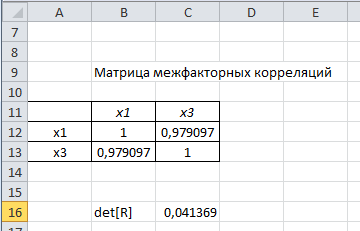



Рис. 2 – Матрица межфакторных корреляций R и значение определителя

---

Определитель матрицы R стремится к нулю, что позволяет сделать предположение об общей мультиколлинеарности факторов. Подтвердим это предположение оценкой статистики Фаррара-Глоубера.

Вычислим наблюдаемое значение статистики Фаррара – Глоубера по формуле:



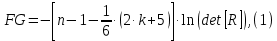
где 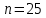– количество наблюдений (заводов); 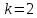– количество факторов (переменных анализа), подставляем значения в формулу (1):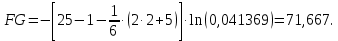



Фактическое значение этого критерия 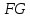сравниваем с табличным значением критерия 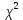с 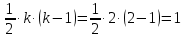степенью свободы и уровне значимости 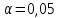. Табличное значение 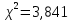можно найти с помощью функции ХИ2.ОБР.ПХ(0,05; 1).

Так как 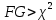(71,667 > 3,841), то в массиве объясняющих переменных существует мультиколлинеарность.

Проверка наличия мультиколлинеарности каждой переменной с другими переменными.

Вычислим обратную матрицу 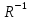с помощью функции MS Excel МОБР (рис. 3).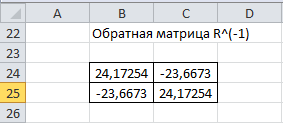



Рис. 3 – Обратная матрица

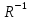
Вычисление F-критериев



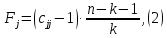
где 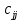– диагональные элементы матрицы 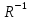(рис. 4).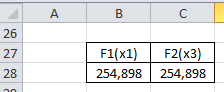



Рис. 4 – Значения F-критериев

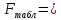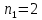Фактические значения F-критериев сравниваются с табличным значением при и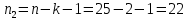

---

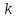степенях свободы и уровне значимости , где – количество факторов.

Так как все значения F-критериев больше табличного, то все исследуемые независимые переменные мультиколлинеарны с другими.

Уточнение набора факторов, наиболее подходящих для регрессионного анализа, осуществим другими методами отбора.

2) Пошаговый отбор факторов методом исключения из модели статистически незначимых переменных

В соответствии с общим подходом, пошаговый отбор следует начинать с включения в модель всех имеющихся факторов, то есть в нашем случае с трёхфакторной регрессии. Но мы не будем включать в модель факторы из заранее известных коллинеарных пар, а также фактор , имеющий слабую связь с . Таким образом, пошаговый отбор факторов начнем с двухфакторного уравнения. Фрагмент двухфакторного регрессионного анализа представлен на рис. 5.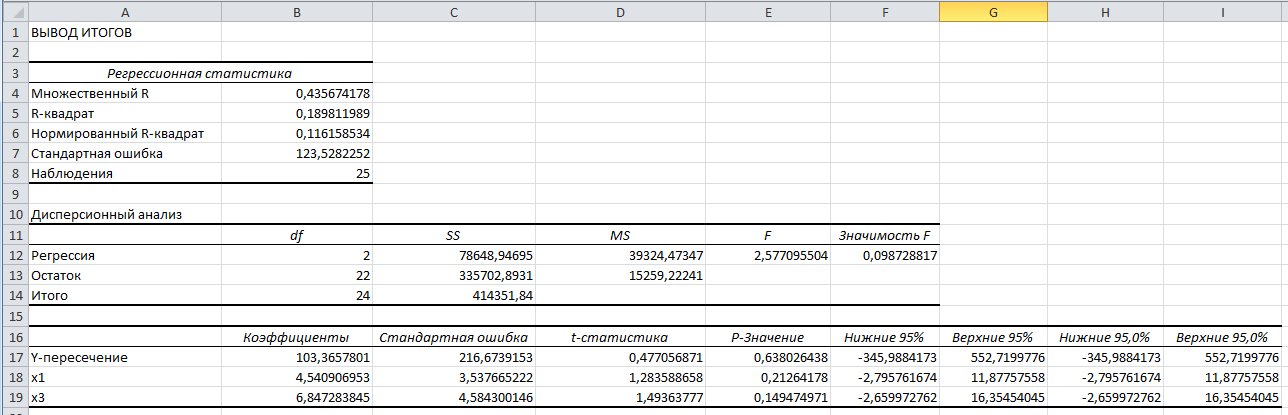



Рис. 5 – Фрагмент двухфакторного регрессионного анализа

Статистически незначимыми 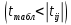оказались три фактора (на рис. 1 они выделены жирным шрифтом). На следующем этапе пошагового отбора удаляем статистически незначимый фактор с наименьшим значением t-критерия, то есть фактор ОА (на рисунке 2 выделен цветом).

Аналогично поступаем до тех пор, пока не получим уравнение, в котором все факторы окажутся статистически значимыми. Этапы получения такого уравнения, то есть фрагменты соответствующих регрессионных анализов, представлены на рисунках 3, 4.

		t табл(0.05;109-4-1=104)=	1.983037471
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	-3255.832024	15398.16512	-0.211442857
ОС	-0.040859333	0.016074384	-2.541891019
ПП	0.650673211	0.062463899	10.41678825
ДО	0.032173752	0.019338145	1.663745481
КО	0.048029464	0.027130844	1.770290058

---