Файл: Содержание Задание 1 Сравнительный анализ метода наименьших квадратов и метода макмального правдоподобия при определении параметров эконометрических моделей. Ответ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– КО по возрастанию фактора 
– ПП (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию ).
2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*109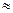
27 значений. В результате получим две совокупности по ½*(109-27)=41 значению соответственно с малыми и большими значениями .
3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 9).
Для первой совокупности:
Для второй совокупности:
Рисунок 9. Фрагменты регрессионного анализа для первой и второй совокупностей соответственно
4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):
5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости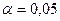
и двумя одинаковыми степенями свободы 
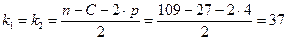(здесь р – число параметров (коэффициентов) в уравнении регрессии):
.
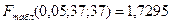Так как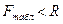
, то обнаруживается наличие гетероскедастичности в остатках модели по отношению к фактору .
Аналогично обнаруживается наличие гетероскедастичности в остатках при упорядочении значений переменных по каждому из двух оставшихся факторов
и 
. Эти процедуры проводятся в полном соответствии с рассмотренной процедурой. Мы их опускаем.
4. Построение доверительных интервалов для результирующей переменной и определение компаний с заниженным и завышенным фактическим уровнем энерговооруженности (производительности «у»). Ранжирование компаний по степени их эффективности на основе результатов моделирования.
5. Оценку степени влияния факторов на результат с помощью коэффициентов эластичности,
и 
коэффициентов. Выбор наиболее влияющего фактора.
6. Построение парной регрессии с наиболее влияющим фактором. Сравнение качества множественной и парной регрессий.
7. Прогнозирование энерговооруженности (производительности
) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения.
8. Графическое представление результатов моделирования.
– ПП (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию ).2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*109
27 значений. В результате получим две совокупности по ½*(109-27)=41 значению соответственно с малыми и большими значениями .3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 9).
Для первой совокупности:
| Дисперсионный анализ | | | |
| | df | SS | MS |
| Регрессия | | | |
| Остаток | | 2.04901E+11 | |
| Итого | | 2.27839E+11 | |
| | | | |
| | Коэффициенты | Стандартная ошибка | t-статистика |
| Y-пересечение | 10965.13577 | 13026.38488 | 0.841763534 |
| ОС | 0.002340442 | 0.040854765 | 0.057286887 |
| КО | -0.09932818 | 0.057414794 | -1.730010202 |
| ПП | -0.220959047 | 0.120684593 | -1.830880326 |
Для второй совокупности:
| Дисперсионный анализ | | | |
| | df | SS | MS |
| Регрессия | | 9.15293E+12 | 3.05098E+12 |
| Остаток | | 1.35495E+12 | |
| Итого | | 1.05079E+13 | |
| | | | |
| | Коэффициенты | Стандартная ошибка | t-статистика |
| Y-пересечение | -72702.62526 | 38053.26016 | -1.910549187 |
| ОС | -0.057544265 | 0.022085349 | -2.60554026 |
| КО | 0.029880567 | 0.034694784 | 0.861240878 |
| ПП | 0.869087051 | 0.10222039 | 8.50209095 |
Рисунок 9. Фрагменты регрессионного анализа для первой и второй совокупностей соответственно
4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):
| R=1.35495Е+12/2,04901Е+11= | 6,612694 |
5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости
и двумя одинаковыми степенями свободы (здесь р – число параметров (коэффициентов) в уравнении регрессии): .Так как
, то обнаруживается наличие гетероскедастичности в остатках модели по отношению к фактору .Аналогично обнаруживается наличие гетероскедастичности в остатках при упорядочении значений переменных по каждому из двух оставшихся факторов
и . Эти процедуры проводятся в полном соответствии с рассмотренной процедурой. Мы их опускаем.4. Построение доверительных интервалов для результирующей переменной и определение компаний с заниженным и завышенным фактическим уровнем энерговооруженности (производительности «у»). Ранжирование компаний по степени их эффективности на основе результатов моделирования.
5. Оценку степени влияния факторов на результат с помощью коэффициентов эластичности,
и коэффициентов. Выбор наиболее влияющего фактора.6. Построение парной регрессии с наиболее влияющим фактором. Сравнение качества множественной и парной регрессий.
7. Прогнозирование энерговооруженности (производительности
) на основе модели парной регрессии с вероятностью 95% при условии, что прогнозное значение фактора увеличится на 10% относительно его среднего значения.
8. Графическое представление результатов моделирования.