Файл: Контрольная работа 1 по дисциплине Анализ денежных потоков Вариант 4 20 июня 2021г. Томск 2021.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 18.10.2024

Просмотров: 9

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство образования и науки РФ

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра экономики

КОНТРОЛЬНАЯ РАБОТА №1

по дисциплине «Анализ денежных потоков»

Вариант №4

«20» июня 2021г.

ТОМСК 2021

  1. Предприниматель взял в банке ссуду на 3 года под процентную ставку 25% годовых. Определить, во сколько раз к концу срока сумма долга будет больше выданной банком суммы, если банк начисляет простые проценты.

Решение:

Используем формулу F = P(1 + n*r), при n = 3, r = 25%,

F = P*(1+3*0,25)=P*1,75.

К концу срока сумма долга будет больше выданной банком суммы в 1,75 раз.


  1. Векселедержатель 1 октября предъявил для учета вексель на сумму 600 тыс. руб. со сроком погашения 25 октября текущего года. Банк учел вексель по простой учетной ставке 20% годовых. Какую сумму получит векселедержатель от банка?

Решение:

Используем формулы D = F – P, P = F*(1-d*t/T), где F = 600 000, d = 0,20, t = 24, T=360,

P = 600000*(1-0,20*24/360)= 592000

D = 600000-592000 = 8000 рубля.

Векселедержатель от банка получит 8000 рублей.


  1. Банк предоставил ссуду в размере 500 тыс. руб. на 33 месяца под процентную ставку 28% годовых на условиях ежегодного начисления процентов. Какую сумму нужно будет вернуть банку по окончании срока при использовании следующих условиях: 1) при расчетах используется схема сложных процентов; б) при расчетах используется смешанная схема?

Решение:

  1. При расчетах использования схемы сложных процентов используем формулу

F = P(1+r)w+f , P = 500000, r = 0,28, w = 2, f = 0,75

F = 500000*(1+0,28)2+0,75= 985819,5

Необходимо будет вернуть сумму 985 819,5 рублей.

  1. При расчетах использования смешанной схемы используем формулу

F = P(1+r)w*(1+f*r), P = 500000, r = 0,28, w = 2, f = 0,75

F = 500000*(1+0,28)2*(1+0,75*0,28)= 991232

Необходимо будет вернуть сумму 991232 рубля.

  1. Долговое обязательство на выплату 2 млн руб. учтено за 2 года до срока. Определить полученную сумму, если производилось: а) полугодовое; б) поквартальное; в) помесячное дисконтирование по сложной учетной ставке 20% годовых.

  1. Используем формулу P = F(1-d/m)m*n , F = 2, d = 0,20, n = 2, m = 2

P = 2*(1-0,20/2)2*2=1,3122.

Полученная сумма составит 1 312 200 руб.

  1. Используем формулу P = F(1-d/m)m*n , F = 2, d = 0,20, n = 2, m = 4

P = 2*(1-0,20/4)4*2= 1,326840863

Полученная сумма составит 1 326 840 руб. 86 коп.

  1. Используем формулу P = F(1-d/m)m*n , F = 2, d = 0,20, n = 2, m = 12

P = 2*(1-0,20/12)12*2= 1,336129617

Полученная сумма составит 1 336 129 руб. 61 коп.

  1. Банком выдан кредит на 9 месяцев под 24% годовых с ежеквартальным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов.

Решение:

По формуле r= , r= 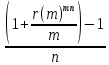, n=0,75, r(m)=0,24, m=3,

, r= 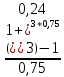=0,252079

Величина эквивалентной простой учетной ставки 25,21%.


  1. Принято решение объединить три платежа стоимостью 10 000 долл., 20 000 долл. и 15 000 долл., срок уплаты которых наступит соответственно через 135, 166 и 227 дней от настоящего момента времени, в один платеж, равный им по сумме. Определить срок консолидированного платежа при использовании простой процентной ставки 8% годовых.

Решение:

Используем формулу простых процентов F = P(1+n*r), принимаем продолжительность года = 360 дней, а x – консолидируемый период,

Тогда:

10000/(1+ 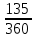*0,08), 20000/*(1+ 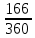*0,08), 15000/(1+ 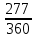*0,08),

10000/(1+ 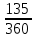*0,08)+20000/(1+ 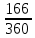*0,08)+15000/(1+ 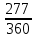*0,08)= 45000*(1+ 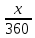*0,08),
X = 195,4
Срок консолидируемого платежа равен 195 дней.


  1. На вклад в 900 тыс. руб. каждые полгода начисляются сложные проценты по номинальной годовой процентной ставке 8%. Оцените сумму вклада через 1,5 года с точки зрения покупательной способности, если ожидаемый темп инфляции—0,5% за квартал.

Решение:

При наращении сложными процентами при полугодовом начислении процентов сумма вклада составит:

F=900000*(1+0,08/2)2*1,5=1012378

Индекс инфляции за 1,5 года при темпе инфляции 0,5% за квартал составит


Iu(1.5)=(1+0,005)6=1,030378

Величина вклада с точки зрения ее покупательской способности равна

Fa= 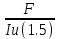= =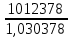982530,7

Вычисляя из этой величины первоначальную сумму вклада, найдем реальный доход владельца вклада:

Fa-P=982530,7-900000=82530,7

  1. В банк на депозит внесено 100 тыс. руб., срок депозита—три года, сложная ссудная ставка равна 8% годовых. Определить ставку налога на начисленные проценты, если после его уплаты у вкладчика осталось 120 тыс. руб.

Решение:

Из формулы Ft=P[(1+r)n* (1-t)+t], выразим ставку налога на проценты

120000=100000*[(1+0,08)3* (1-t)+t],

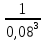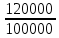t=1- *( -1)

Ставка налога ровна 3,9%

  1. В начале каждого года вы вкладываете 500 тыс. руб. в банк, ежегодно начисляющий сложные проценты по ставке 9% годовых. Определить сумму, которая накопится на счете через 5 лет. Если эта сумма получается в результате однократного помещения денег в банк, то какой величины должен быть взнос?

Решение:

При А=500, r=9%, n=5,

FVpst=500*FM3(9%,5)=500*5,984711=2992,356

Величина первоначального взноса должна составлять 2 992,356 тыс. руб.

  1. Какую сумму необходимо положить в банк, чтобы в течение 8 лет иметь возможность снимать со счета по 3000 в конце каждого полугодия и за 8 лет исчерпать счет полностью, если банк ежеквартально начисляет сложные проценты по ставке 10% годовых?

Решение:

При А=3000, r=10%, n=8, m=4

PVpst=3000* 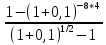=58553,17

Необходимо положить в банк 58533,17.

Смотрите также файлы