Министерство образования Республики Беларусь

Белорусский национальный технический университет

Кафедра «Горные машины»
КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

Разработка программы на Pascal 7.0


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Руководитель Витушко Е.А.
Исполнитель студент группы 30205121

Щипачёв Д.С.
2022
Задание по курсовому проектированию

Разработать программу зеркального отображения двухмерного массива (N*N) относительно горизонтальной оси симметрии.

Содержание

Введение……………………………………………………………… 3

1. 
   Постановка задачи…………………………………………………….. 4
   
2. 
   Математическая формулировка задачи……………………………… 5
   
3. 
   Алгоритмизация задачи …………………………………………...…. 10
   
4. 
   Идентификаторы программы………………………………………… 11
   
5. 
   Блок – схема алгоритма………………………………………………. 12
   
6. 
   Текст исходной программы………………………………………….. 15
   
7. 
   Результаты выполнения программы………………………………… 18
   
8. 
   Анализ результатов……………………………………………...……. 20
   
9. 
   Инструкция по работе с программой…………………………...…… 21
   

Заключение……………………………………………………………. 22

Список использованных источников……… ……………………….. 23

Введение

Перед выполнением работы необходимо изучить правила описания и использования переменных типа массив, типизированных констант типа массив.

В данной пояснительной записке проводится описание последовательности шагов по составлению программы на алгоритмическом языке Turbo Pascal 7.0 и результаты применения этой программы для вычисления «Зеркального отображения элементов двухмерного массива относительно горизонтальной оси симметрии».

Рассматриваются вопросы математической формулировки и алгоритмизации задачи, разработки блок-схемы алгоритма её решения, составления исходной Pascal-программы и реализации вычислений по составленной программе.

Ввод исходных данных и вывод результатов вычисления выполняется в отдельном для каждого вычисления окне.

1. 
   Постановка задачи
   

Ставится задача составить программу вычисления на алгоритмическом языке Turbo Pascal 7.0. «

---

Зеркальное отображение элементов двухмерного массива относительно горизонтальной оси симметрии».

2. 
   Математическая формулировка задачи
   

Массив - это структурированный тип данных, который используется для описания упорядоченной совокупности фиксированного числа элементов одного типа, имеющих общее имя. Для обозначения элементов массива используются имя переменной-массива и индекс. Массив - это структура однотипных данных, расположенная в памяти одним неразрывным блоком.



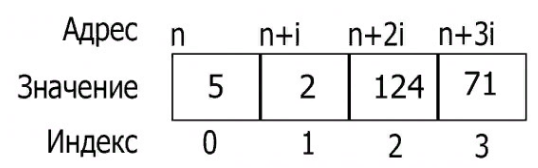
Рис.1. Расположение одномерного массива в памяти

Многомерные массивы хранятся точно также.



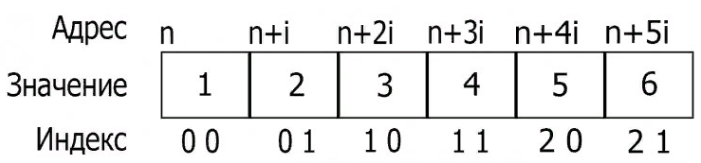
Рис.2. Расположение двухмерного массива в памяти

Знание этого позволяет нам по-другому обращаться к элементам массива.

Изображения - это целый комплекс из разных заголовков и информации о изображении, и самого изображения хранящемся в виде двухмерного массива.

Для того чтобы перевернуть изображение по горизонтали нужно всего лишь читать массив, в котором оно содержится сверху вниз и справа налево.

Зеркальная (отражающая) матрица - это матричное преобразование в плоскости измерения n-1 в n-мерном пространстве. Распространенными сценариями применения являются обработка изображений в 2D-пространстве и преобразование сцены в 3D-пространстве. Сначала посмотрим на эффект зеркального преобразования:



Рис.3. Зеркальная (отражающая) матрица.

После интуитивного ощущения эффекта зеркального преобразования давайте посмотрим, как выглядит математическое выражение этого преобразования. Прежде всего, зеркальное преобразование n-мерного пространства основано на определенной n-1 плоскости измерений (прямая линия для 2-мерного измерения). Знание линейной алгебры знает, что в n-1 плоскости измерений n-мерного пространства есть нормальные векторы. u=(u

---

₁,u₂,...,u_n). Чтобы сделать единичный вектор нормали плоскости зеркала, единичный вектор нормали || u || = 1, определить матрицу зеркала Q = I -2uu^T.

1. Q является симметричным и стандартным ортогональным, Q^T = (I -2uu^T)^T = I - 2uu^T . Q симметричен. Q^TQ = I - 4uu^T+4uu^Tuu^T=I. Q является стандартным ортогональным. Принципы матричных операций, мы также можем расширить Q:



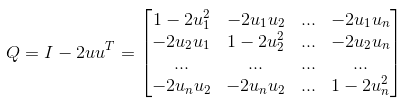
Из формы расширения матрицы Q ясно, что Q_ij = Q_ji = -2u_iu_j, i≠ j, Значит, Q симметричен. Стандартное ортогональное: q

---

_i, q_j. Это два столбца Q, которые определены стандартной ортогональностью и должны удовлетворять следующим условиям:



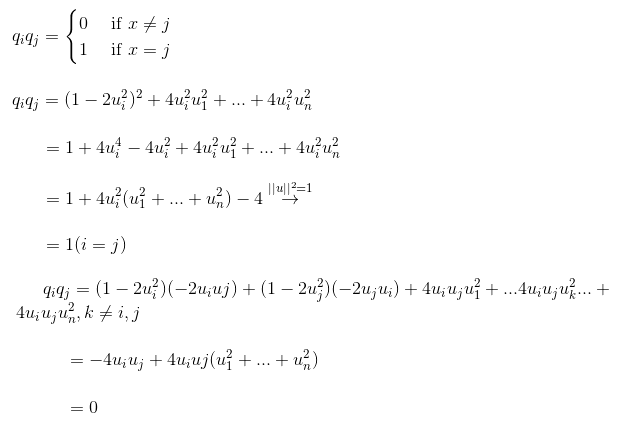
2. Q² = Q^TQ = I, Это свойство отражает характеристики зеркального отображения, зеркальное отображение в два раза больше исходного пространства.

Выше приведено определение матрицы зеркального отображения и некоторых ее свойств и производных, поэтому давайте подумаем немного глубже: почему выражение зеркального отображения является матричным преобразованием, и если я выполняю вращение, это матричное преобразование? Прежде всего, ответ на вопрос 2: ДА, матрица преобразования вращения в 2-мерном пространстве имеет вид:



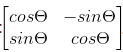
Для задачи 1 суть матричного преобразования можно понимать как преобразование системы координат. Для зеркалирования и вращения мы используем новые координаты для векторов в исходной системе координат (точки в системе координат могут быть выражены как вектор, в котором начало координат указывает на точку). Основы в системе показаны. Например, базовыми векторами координат двумерной прямоугольной системы координат x, y являются (1, 0) и (0, 1). Если вы используете матрицу для представления: 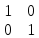. Базовый вектор - это вектор-столбец матрицы, координаты (x, y)(1,1) системы координат точки задаются системой уравнений. 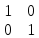* 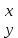= 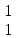. Найти(x, y) = (1,1), потому что в исходной системе координат предположим, что мы зеркально отражаем точку (1, 1) вдоль оси X. Зеркало здесь очень простое. Ось X совпадает с исходной системой координат. Y Ось противоположна исходной системе координат, поэтом базовые векторы новой системы координат после зеркального отображения равны (1,0) и (0, -1) (Если вы можете получить тот же ответ через приведенную выше формулу зеркального отображения, u = (0, 1)), матричное представление новой системы координат 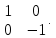Координаты точки (1,1) в исходной системе координат в новой системе координат имеют уравнения 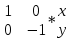= Find (x, y) = (1, -1), что совпадает с нашим интуитивным восприятием.

---

Зеркально отразим некую прямую линию в 2-мерном пространстве. Предположим, что единичный вектор нормали u (x, y) прямой по Q = I-2uu^T. Рассчитаем зеркальную матрицу в 2-мерном пространстве:



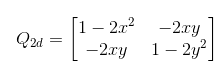
3. Алгоритмизация задачи

В соответствии с постановленной в разделе 2 задачей целесообразно реализовать алгоритм программы.

Алгоритм работы головной программы следующий:

1. 
   Вывести в специальном окне заставку программы, содержащую сведения о назначении программы, исполнителе и руководителе курсовой работы, а также подсказку для пользователя о последующих действиях.
   
2. 
   Создать окно для ввода исходных данных.
   
3. 
   Ввести значение n.
   
4. 
   Присвоить первоначальному значению n максимальный размер матрицы а[1;n].
   
5. 
   Организовать цикл для заполнения исходной матрицы а[1;n] не больше nmax = 15;
   
6. 
   Выполнить. Заполняем случайными числами матрицу.
   
7. 
   Вызов процедуры для горизонтального отражения матрицы Otraz(a, n).
   
8. 
   Вывести результаты вычислений в новом окне.
   
9. 
   Закончить выполнение программы.
   

3. 
   Идентификаторы программы
   

Для указания соответствия обозначений переменных в формулах математической формулировки и их идентификаторов в программе сведем их в таблицу 1:
Таблица 1

Обозначение параметров		Смысл параметра
В формулах	В программе
Q	mtr	Исходная матрица для преобразования
Q2	a	Матрица для преобразованная
i	n	Индекс матрицы
j	n	Индекс матрицы

5. Блок-схема алгоритма

5.1. Блок-схема алгоритма головной программы

---

Смотрите также файлы

• Какое решение следует вынести Конституционному Суду.docx

• Контрольная работа дисциплина Психологический тренинг Ф. И. О студента Монгуш Юлиана Владимировна.doc

• Лабораторная работа по дисциплине Гражданское Право Группа Лб20Ю171в Студент Н. А. Жаркая Преподаватель.docx

• Реферат по дисциплине Финансовый контроль.docx

• Невеста Родители невесты.docx