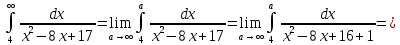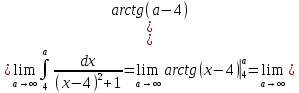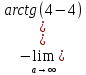Задание 1. Найти уравнения и выполнить построение линий уровня

функций:



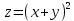
Решение:

Уравнение линий уровня имеют вид:



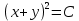
Рассмотрим некоторые из них:



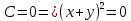
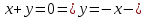прямая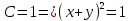



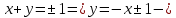две прямые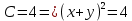



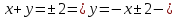две прямые

Таким образом, линии уровня представляют собой семейство прямых, параллельных прямой .

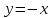Построим линии уровня:



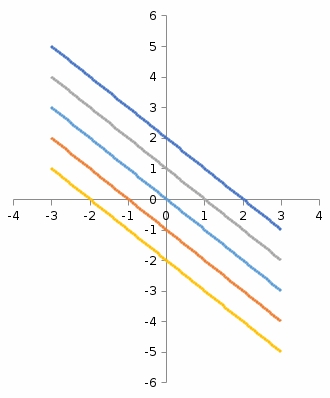
Задание 2. Найти частные производные первого порядка:



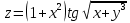
Решение:















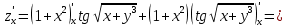
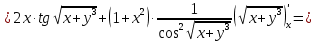
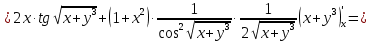
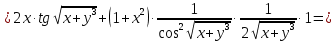
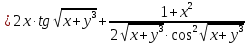
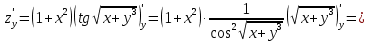
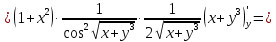
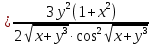
Задание 3. Найти стационарные точки и исследовать на экстремум

функции:



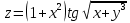
Решение:



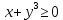
Решим систему:

---

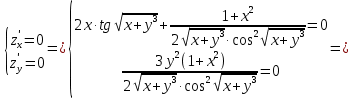
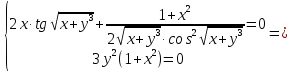
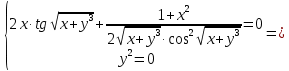
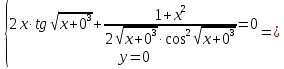
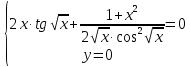
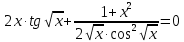
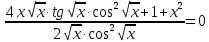
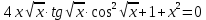
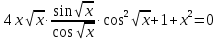
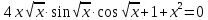
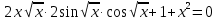
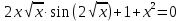
Из условий и 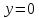следует, что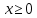

Учитывая ограниченность функции



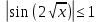
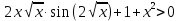
Таким образом, уравнение 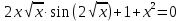решений не имеет.

А значит, исходная функция экстремумов не имеет.

Задание 4. Найти производную z(x, y) по направлению вектора l в

точке М:



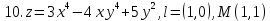
Решение:

Производная по направлению имеет вид:















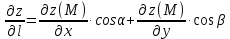
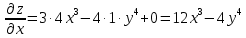
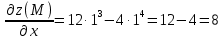
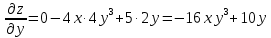
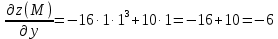
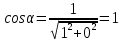
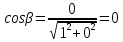
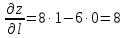
Задание 5. Найти интегралы:







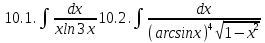
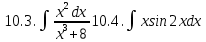
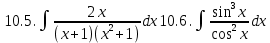
Решение:

---

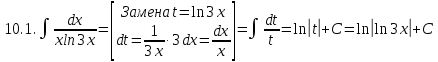
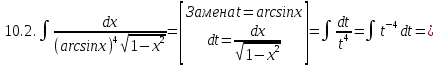
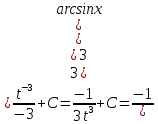
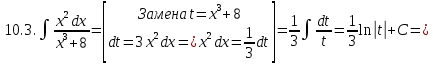
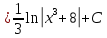
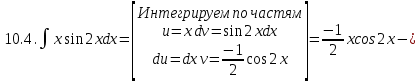
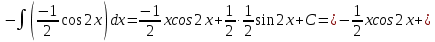
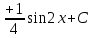
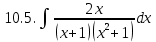
Разложим подынтегральное выражение на простейшие дроби:
























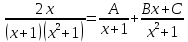
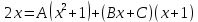
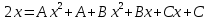
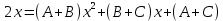
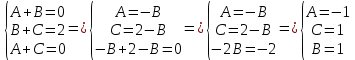
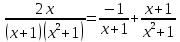
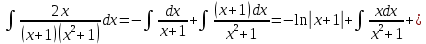
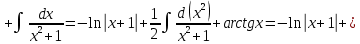
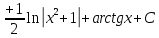
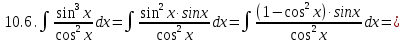
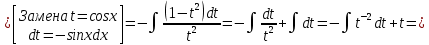
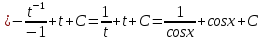
Задание 6. Вычислить интегралы:



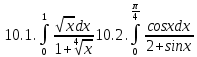
Решение:




















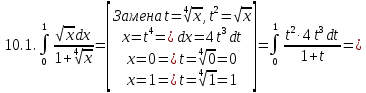
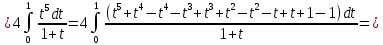
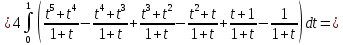
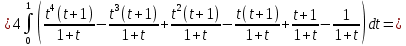
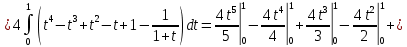
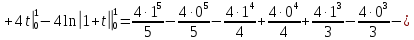
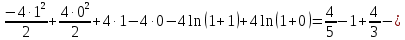
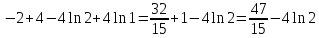
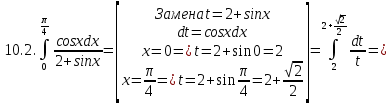
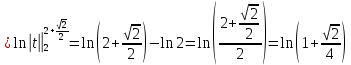
Задание 7. Вычислить площади фигур, ограниченных линиями:

---

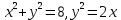
Решение:

Построим фигуру, площадь которой требуется найти:

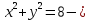окружность с центром в точке (0;0) радиуса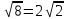

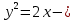парабола, ветви вправо.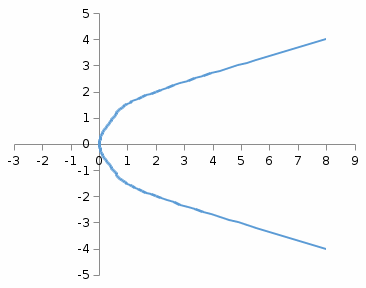


Т.к. фигура симметрична относительно оси Ох, следовательно, можно найти площадь половины фигуры и умножить ее на 2.

Найдем пределы интегрирования:















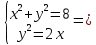
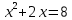
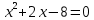
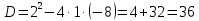
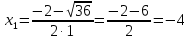
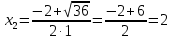
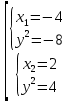
Первая система решений не имеет, решениями второй системы являются точки (2;2), (2;-2)
















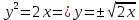
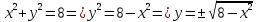
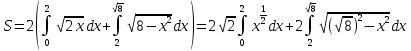
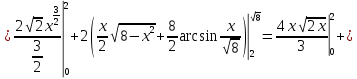
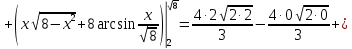
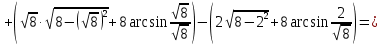
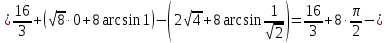
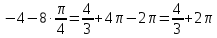
Задание 8. Вычислить или установить расходимость несобственных

интегралов:



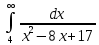
Решение:

---

Смотрите также файлы

• Экзамена задача 1.docx

• Пз 1 формирование профессиональной готовности будущего классного руководителя к ценностносмысловому взаимодействию с семьёй школьника.docx

• Правописание Что такое наречие.pptx

• анемии.docx

• Бронхиальная астма.docx