На шестом этапе менеджерами оцениваются альтернативы на основе информации, предоставленной аналитиками, и дополнительной (субъективных суждений, мнений акционеров и т.п.). При этом используются результаты аналитических расчетов различных вариантов, рисков, а также личный опыт менеджеров и их интуиция. Появляется суждение управляющего о предпочтительности вариантов достижения целей. Если менеджер сомневается в выборе наилучшей альтернативы, организуются оценка эффективности решения и получения дополнительной информации на основе эксперимента.

На седьмом этапе окончательно принимается и оформляется решение.

Восьмым этапом является реализация управленческого решения.

Поиск таких решений является многошаговым, в ходе его постоянно сравниваются цели с возможностями их достижения, отыскиваются новые возможности, корректируются цели в сторону увеличения (усложнения), если выявлены дополнительные ресурсы, и в сторону снижения, если первоначально сформулированные цели оказались нереальными. Следовательно, решение таких проблем тесно связано с анализом условий и целей действия.
Ход работы
В качестве лабораторной работы выбран вариант 1.

Найти наилучшие стратегии по критериям: Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Гурвица применительно к матрице рисков (коэффициент пессимизма равен 0,4) для следующей платежной матрицы игры с природой (элементы матрицы - выигрыши):



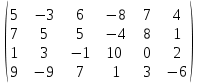
1. Решение задачи при помощи Excel.

1.1. Критерий Ваальда

Из альтернатив aj выберем ту, которая при самом неблагоприятном состоянии внешней среды, имеет наибольшее значение показателя.

С этой целью в каждой строчке матрицы фиксируют альтернативы с минимальным значением показателя и из отмеченных минимальных выберем максимальное при помощи формулы =МИН(B1:G1) (рисунок 1).



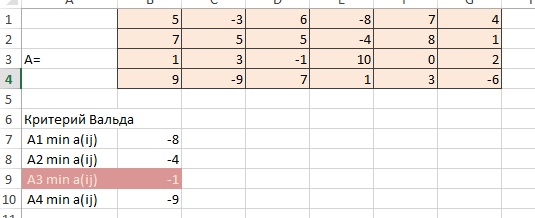
Рисунок 1 – Критерий Ваальда
Самой оптимальной по правилу максимина является стратегия №3.

1.2. Критерий Сэвиджа

Построим матрицу рисков по формуле =МАКС(B$1:B$4)-B1, то есть определим отклонение от лучшего результата каждой отдельной графы по maxiXij – Xij. (рисунок 2).

---

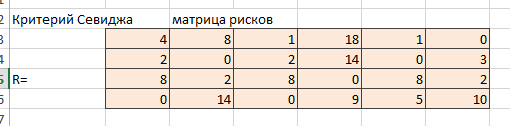
Рисунок 2 – Матрица рисков для критерия Сэвиджа
По формуле minmaxП = mini [maxj (maxiXij – Xij)] найдем решение, при котором максимальное сожаление будет меньше других (рисунок 3).



Рисунок 3 – Решение по критерию Сэвиджа
Таким образом, по критерию Сэвиджа наиболее оптимальной является стратегия №3.

1.3. Критерий Гурвица

Рассчитаем критерий по платежной матрице, где коэффициент пессимизма равен 0,2. Для этого используем формулу а* = maxi [(1-p) minj Пji+ pmaxj Пji].

Полученные значения представлены на рисунке 4, где minj Пjiрассчитываем как =МИН(B1:G1), maxj Пjiрассчитываем как =МАКС(B1:G1).



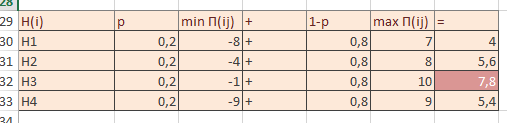
Рисунок 4 – Критерий Гурвица для платежной матрицы
Таким образом, самой оптимальной стратегий для платежной матрицы по критерию Гурвица является №3.

Рассчитаем критерий по матрице рисков, где коэффициент пессимизма равен 0,4. Для этого используем формулу а* = mini [(1-p) minj rji+ pmaxj rji] (рисунок 5).


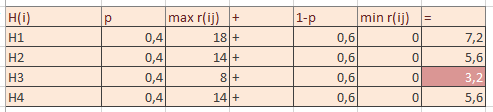
Рисунок 5 – Критерий Гурвица для матрицы рисков
Таким образом, оптимальным решением является стратегия №3.

Исходя из полученных результатов, самым оптимальным решением, полученных из расчетов в MS Excel, является стратегия №3.

2. Решение задачи при помощи MathCAD представлены на рисунках 6-10.



Рисунок 6 – Решение по критерию Ваальда

Рисунок 7 – Решение по критерию Сэвиджа, часть 1


Рисунок 8 – Решение по критерию Сэвиджа, часть 2


Рисунок 9 – Решение по критерию Гурвица, часть 1

---

Рисунок 10 – Решение по критерию Гурвица, часть 2
Таким образом, посредством MathCAD получаем аналогичный результат – решение №3 по всем критерием является наиболее оптимальным.

3. Решение вручную представлено на рисунках 11-12.



Рисунок 11 – Критерии Ваальда и Сэвиджа


Рисунок 12 – Критерий Гурвица
Таким образом, исходя из результатов, полученных ручным расчётом, оптимальным решением обладает стратегия №3.

Расчеты, произведенные вручную и произведенные автоматизированно(при помощи Excel и MathCAD), абсолютно идентичны.

Результат Excel – стратегия №3 самая оптимальная.

Результат MathCAD – стратегия №3 самая оптимальная.

Результат, полученный вручную, – стратегия №3 самая оптимальная.

Таким образом, оптимальное решение заключается в стратегии №3.

Вывод: в ходе решения лабораторной работы освоены и закреплены практические навыки по принятию и обоснованию управленческих решений в условиях недостатка информации, когда одним из игроков не имеет конкретной цели и случайным образом выбирает очередные «ходы».

---

Смотрите также файлы

• Техникоэкономическое обоснование проекта.docx

• Российский государственный социальный университет практическое задание 4 по дисциплине Биология.docx

• С июня 1992 Российский государственный архив фонодокументов (ргафд).docx

• Российский государственный архив фонодокументов выполнила студентка группы гд41 Семенченко Альбина.pptx

• Бокс любимый вид спорта.pptx