Файл: Отчет по лабораторной работе 1 Массивы и матрицы в Scilab. Решение задач линейной алгебры.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное агентство по образованию «Санкт-Петербургский государственный университет телекоммуникаций им.проф.М.А.Бонч-Бруевича (СПбГУТ)»
Факультет Информационных систем и технологий (ИС и Т)
Кафедра: Информатики и компьютерного дизайна (ИКД)
По дисциплине «Теория информации, данные, знания»
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № «1»
«Массивы и матрицы в Scilab. Решение задач линейной алгебры»
Автор:		(подпись)	(Ф.И.О.)
Оценка:
Дата:
Руководитель проекта:		(подпись)	/. / (Ф.И.О.)
		Санкт-Петербург 2022

---

Содержание

Задание 1.1:

Решить систему линейных алгебраических уравнений, сделать проверку.
Система линейных алгебраических уравнений:



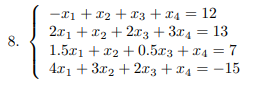
Задание 1.2:

Если возможно, вычислить матрицу, обратную к матрице D:

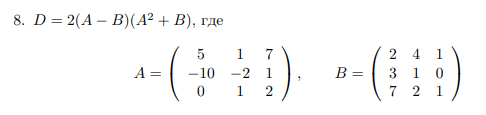
Теоретический материал:

Ввод и формирование массивов и матриц.

Задать одномерный массив в Scilab можно следующим образом:

Name = Xn:dX:Xk

где name — имя переменной, в которую будет записан сформированный массив, Xn — значение первого элемента массива, Xk — значение последнего элемента массива, dX — шаг, с помощью которого формируется каждый следующий элемент массива, т.е. значение второго элемента составит Xn+dX, третьего Xn+ dX+dX и так далее до Xk.

Если параметр dX в конструкции отсутствует, это означает, что по умолчанию он принимает значение, равное единице, т.е. каждый следующий элемент массива равен значению предыдущего плюс один:

Name = Xn:Xk

Переменную, заданную как массив, можно использовать в арифметических выражениях и в качестве аргумента математических функций.

Еще один способ задания векторов и матриц в Scilab — это их поэлементный

ввод. Так, для определения вектора-строки следует ввести имя массива, а затем после знака присваивания, в квадратных скобках через пробел или запятую, перечислить элементы массива:

name = [x1 x2 ... xn] или name = [x1, x2, ..., xn]

Элементы вектора-столбца вводятся через точку с запятой:

Name = [x1; x2; ...; xn]

Обратиться к элементу вектора можно, указав имя массива и порядковый номер элемента в круглых скобках:

name(индекс)

Ввод элементов матрицы также осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:

Name = [x11, x12, ..., x1n; x21, x22, ..., x2n; ...;

---

xm1, xm2, ..., xmn;]

Обратиться к элементу матрицы можно, указав после имени матрицы, в круглых скобках через запятую, номер строки и номер столбца на пересечении которых элемент расположен:

name(индекс1, индекс2)

Важную роль при работе с матрицами играет знак двоеточия «:». Указывая его вместо индекса при обращении к массиву, можно получать доступ к группам его элементов.

Действия над матрицами

Для работы с матрицами и векторами в Scilab предусмотрены следующие операции:

+ — сложение;

- — вычитание;

’ — транспонирование;

* — матричное умножение;

* — умножение на число;

ˆ — возведение в степень;

\ — левое деление;

/ — правое делениe;

.* — поэлементное умножение матриц;

.ˆ — поэлементное возведение в степень;

.\ — поэлементное левое деление;

./ — поэлементное правое деление.

Некоторые из специальных матричных функций.

Для работы с матрицами и векторами в Scilab существуют специальные функции. Рассмотрим наиболее часто используемые из них. Функции определения матриц:

• 
  matrix(A [,n,m]) — преобразует матрицу A в матрицу другого размера;
  
• 
  ones(m,n) — создает матрицу единиц из m строк и n столбцов;
  

• 
  zeros(m,n) — создает нулевую матрицу из m строк и n столбцов;
  
• 
  eye(m,n) — формирует единичную матрицу3 из m строк и n столбцов;
  
• 
  det(M) — вычисляет определитель квадратной матрицы М;
  
• 
  rank(M[,tol]) — вычисление ранга матрицы M 1 с точностью tol;
  
• 
  inv(A) — вычисляет матрицу, обратную к данной на основе LU разложения;
  
• 
  ref(A) — осуществляет приведение матрицы A к треугольной форме, используя метод исключения Гаусса;
  

Решение систем линейных алгебраических уравнений

Система m уравнений с n неизвестными вида:

a11x1 + a12x2 + · · · + a1nxn = b1 ,

a21x1 + a22x2 + · · · + a2nxn = b2 ,

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

am1x1 + am2x2 + · · · + amnxn = bm

называется системой линейных алгебраических уравнений (СЛАУ), причем xj — неизвестные, aij — коэффициенты при неизвестных, bi — свободные коэффициенты (i = 1 . . . m, j = 1 . . . n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A · x = b, где x — вектор неизвестных, A — матрица коэффициентов при неизвестных или матрица системы, b — вектор свободных членов системы или вектор правых частей. Совокупность всех решений системы (x1, x2, . . . , xn) называется множеством решений или просто решением системы.

---

Правило Крамера:

Если определитель ∆ = det A матрицы системы из n уравнений с n неизвестными A · x = b отличен от нуля, то система имеет единственное решение x1, x2, . . . , xn, определяемое по формулам Крамера: xi = ∆i/∆, где ∆i — определитель матрицы, полученной из матрицы системы A заменой i-го столбца столбцом свободных членов b.

Ответы на задания

Задание 1.1

Дана система линейных уравнений, в которой число неизвестных равно числу уравнений. Составим две основные матрицы:



Проверим делитель основной матрицы А:



Так как он отличен от нуля, можно решить СЛАУ с помощью метода Крамера. В книге «Scilab. Решение инженерных и математических задач» представлен текст файла сценария с решением задачи по формулам Крамера:

Текст файла-сценария решения СЛАУ методом Крамера

//Матрица коэффициентов:

A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];

b=[8;9;-5;0]; //Вектор свободных коэффициентов

A1=A;A1(:,1)=b; //Первая вспомогательная матрица

A2=A;A2(:,2)=b; //Вторая вспомогательная матрица

A3=A;A3(:,3)=b; //Третья вспомогательная матрица

A4=A;A4(:,4)=b; //Четвертая вспомогательная матрица

D=det(A); //Главный определитель

//Определители вспомогательных матриц:

d(1)=det(A1); d(2)=det(A2); d(3)=det(A3); d(4)=det(A4);

x=d/D //Вектор неизвестных

P=A*x-b //Проверка

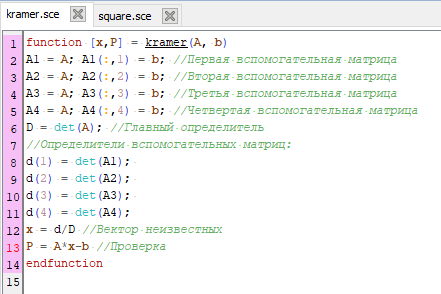
Основываясь на этом сценарии, создадим функцию, которая будет решать уравнение и проверять решение.

Текст функции, реализующей решение СЛАУ методом Крамера с проверкой в конце:



Вызов функции и ее результат:



Система решена, проверка верна.

Задание 1.2

Если возможно, найти матрицу, обратную матрице D:



Объявим матрицы А и В:

---

Найдем матрицу D:



Обратная матрица — такая матрица A’, при умножении на которую исходная матрица A даёт в результате единичную матрицу E.

Матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю.

Найдем определитель матрицы D:



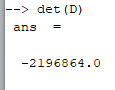
Определитель не равен нулю, следовательно матрица невырождена.

Найдем матрицу Dx, обратную матрицe D и выполним проверку:



Результат проверки – две матрицы, близкие к единичным, следовательно – проверка верна.

Вывод:

Выполняя лабораторную работу, мы научились работать с массивами и матрицами в Scilab, а так же решать некоторые задачи линейной алгебры.

---