Файл: А. Г. Мерзляк и др. Разработано учителем математики моу сош п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной п. Аджером, 2019 Темы домашних зачётных работ Решение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Домашние зачётные работы
по АЛГЕБРЕ
Класс: 7
УМК: А.Г. Мерзляк и др.
Разработано учителем математики
МОУ «СОШ» п. Аджером Корткеросского района
Республики Коми Мишариной Альбиной Геннадьевной
п. Аджером, 2019
Темы домашних зачётных работ:
№1. Решение линейных уравнений
№2. Целые выражения
№3. Функции
№4. Системы линейных уравнений с двумя переменными

Зачётная работа №1. Решение линейных уравнений
-
Решить уравнения
Решение уравнений без скобок
1). х + 16 = 7 2). х + 5,8 = - 4,7 3). 5,5 – х = 12,9
4). – 8,8 – х = - 3,7 5). х – 9,21 = - 4,3 6). х – 4,7 = - 2,34
7). 4,8 – х = 16,3 8). х + 12 = 5 9). – 5,4 – х = - 3,5
10). х + 6,2 = - 7,8 11). 2х = 18 - х 12). 7х + 3 = 30 – 2х
13). 7 – 2х = 3х – 18 14). 0,2х + 2,7 = 1,4 – 1,1х
15). 5,4 – 1,5х = 0,3х – 3,6 16). 11х = 36 – х
17). 9х + 4 = 48 – 2х 18). 8 – 4х = 2х – 16
19). 0,4х + 3,8 = 2,6 – 0,8х 20). 6,8 – 1,3х = 0,6х – 2,7
Решение уравнений со скобками
1). 4(х - 6) = х - 9 2). 6 – 3(х + 1) = 7 – х
3). (8х + 3) – (10х + 6) = 9 4). 14х – 14 = 7(2х - 3) +7
5). 3(х - 2) = х + 2 6). 5 – 2(х - 1) = 4 – х
7). (7х +1) – (9х + 3) = 5 8). 3,4 + 2у = 7(у – 2,3)
9). 4(5х + 2) = 10(3х - 3) + 15 10). 2(7х - 7) = 7(2х - 3) + 7
11). 5,6 – 3(2 – 0,4х) = 0,4(4х - 1) 12). 5(х - 12) = 6(х - 10) – х
13). 0,3(8 – 3у) = 3,2 – 0,8(у - 7) 14). 4(х - 1) = 2(2х - 8) + 12
15). 8(5 – 3х) = 6(2 – 4х) + 7 16). 7(4х - 1) = 6 – 2(3 – 14х)
17). 4 - 6(х + 2) = 3 – 5х 18). (5х + 8) – (8х + 14) = 9
19). -7(х + 3) + 9 = 5 – 6х 20). –(11х - 7) + (7х + 9) =
-
Решить задачи с помощью уравнений
1). Скорость автомобиля на 30 км/ч больше скорости мотоцикла. Они едут навстречу друг другу из пунктов А и В, расстояние между которыми 240 км, и встречаются в пункте С. Найдите скорость автомобиля и скорость мотоцикла, если известно, что автомобиль был в пути 3 часа, а мотоцикл 2 часа.
2). Одна из сторон равнобедренного треугольника на 6 см длинее другой. Найдите боковую сторону треугольника
, если его периметр равен 39 см (рассмотрите 2 случая).
3). В жилом доме 9 однокомнатных, 18 двухкомнатных и 9 трёхкомнатных квартир общей площадью 1458 м². Известно, что площадь двухкомнатной квартиры на 10 м² больше, чем площадь однокомнатной, и на 12 м² меньше, чем площадь трёхкомнатной. Найдите площадь каждой квартиры.
4). Проволоку длиной 456 м разрезали на 3 части, причём первая часть в 4 раза длиннее третьей, а вторая – на 114м длиннее третьей. Найдите длину каждой части проволоки.
5). Ученик задумал число. Если его умножить на 4, а к произведению прибавить 8 и полученную сумму поделить на 2, то получится 10. Какое число задумал ученик?
6). Найдите три последовательных нечётных числа, сумма которых равна 81.
-
Решить уравнения.
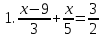
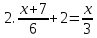
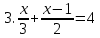
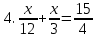
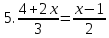
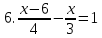 7
7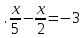 8
8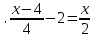
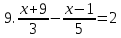 10
10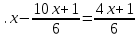
Зачётная работа №2. Целые выражения
-
Степень и его свойства
1). Упростить выражение
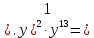 |
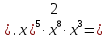 |
| 3). в ∙ 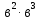 = = |
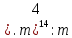 = = |
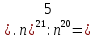 |
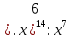 : : 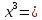 |
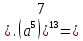 |
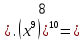 |
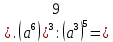 |
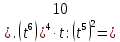 |
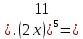 |
| 12). 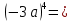 |
2). Вычислить
а)
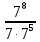 б)
б) 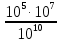 в)
в) 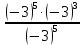 г)
г) 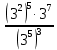 д)
д) 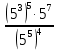
е)
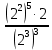 Ж)
Ж) 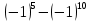 з)
з) 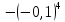 и)
и) 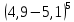
к)
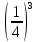
2. Действия с одночленами и многочленами.
1). Сложение и вычитание многочленов.
а) (1 + 3а) + (а² - 2а) б) (7,3у - у² + 4) + 0,5у² + (8,7у – 2,4у²)
в) (х² - 5х) + (5х – 2х²) г) (в² - в + 7) – (в² + в + 8)
д) (8с³ - 3с²) - (7 + 8с³ - 2с²) е) (а² + 5а + 4) – (а² + 5а - 4)
ж) (а² - 5ав) – (7 – 3ав) + (2ав - а²)
з) 6ху – 2х² - (3ху + 4х² +1) – (- ху – 2х² - 1)
и) – (2ав² - ав + в) + 3ав² - 4в – (5ав - ав²)
к) (ху + х² + у²) – (х² + у² - 2ху) – ху
2). Умножение одночлена на многочлен.
а) 3(2х - 1) + 5(3 - х) б) 14(7х - 1) – 7 (14х + 1)
в) 5а(1 + 2а - а²) г) – 3х²(- х³ + х - 5)
д) 4х(х - 1) - 2(2х² - 1) е) 7в(4с - в) + 4с(с – 7в)
ж) -2у(х³ - 2у) – 3(х³у + 4у²)
з) ах(2х – 3а) – х(ах + 5а²)
3). Умножение многочлена на многочлен.
а) (х + с)(у + к) б) (а - в)(х + у) в) (а - х)(в - у)
г) (х + 8)(у - 1) д) (в - 3)(а - 2) е) (- а + у)(- 1 - у)
ж) (2у - 1)(3у + 2) з) (5х - 3)(4 – 3х) и) (х² + у)(х + у²)
к) (5х² - 4х)(х + 1) л) (х² + ху - у²)(х + у) м) (3у - 4)(у² - у + 1)
4). Решить уравнения.
а) (2х - 6)(8х + 5) + (3 – 4х)(3 + 4х) =55
б) (х + 2)(х + 1) – (х - 3)(х + 4) = 12
в) (- 4х + 1)(х - 1) – х = (5 – 2х)(2х + 3) - 17
г) (х + 10)(х - 5) – (х - 6)( х + 3) = 16
д) (2х - 3)(4х + 3) – 8х² = 33
е) 21х² - (3х - 7)(7х - 3) = 37
3.Разложение многочленов на множители
-
Вынесение за скобку
а) 3а – ав б)
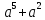 в) 21а²в + 28ав²
в) 21а²в + 28ав² г) – 6х³у² - 9 х²у – 18ху² д) х(2а – 5в) + у(2а – 5в)
е) 5х(в - с) – (с - в) ж) (а - 4)² - 5(а - 4)
з) 2у(а - в) + (в - а) и) (х + 3)² - 3(3 + х)
к)
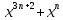 , где n - натуральное число
, где n - натуральное числол)
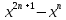
, где n - натуральное число
-
Группировка
а) ав + ас + хв + хс б) ав – ас + ув – ус
в) 4х – ху – 4 + у г) 6ав – 3а + 2в – 1
д) 10ав – 2а + 5в² - в е)
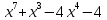
ж)
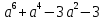 з) 6х – ху – 6 + у
з) 6х – ху – 6 + у и) Вычислите значение выражения
18,2 ∙ 8,1 + 23,8 ∙ 5,1 – 18,2 ∙ 7,6 – 23,8 ∙ 4,6
к) Вычислите значение выражения
32,4 ∙ 6,7 + 17,6 ∙ 8,3 – 32,4 ∙ 1,7 – 3,3 ∙ 17,6
-
ФСУ
а) Представить в виде многочлена (раскрыть скобки)
1). (х - 2)(х + 2) 2). (3х + у)(3х - у) 3). (а² - 3)(а² + 3)
4). (х + 2)² 5). (5 - у)² 6). (х + 7)² + (х + 2)(х - 2)
7). (а + 1)(а - 1) – (а + 4)² 8). (х - 5)² - (х - 7)(х + 7)
9). (с - у)(с + у)(с² + у²) 10). (х - 10)(х² + 100)(х + 10)
б) Упростить выражение
1). 7(х + 8) + (х + 8)(х - 8) 2). (х - 3)(3 + х) + (х - 3)2
3). (у - 5)2 – (у + 7)2 4). (х + 3)(х - 3) – х2 + 2х
5). (2х + 3)(2х - 3) – 3х2 6). (3х - 2)(3х + 2) – (1 + х)(х - 1)
7). (х - 2)2 - 2(х - 2)(х + 2) + (х + 2)2
8). Упростить выражение и найти его значение
(х - 4)2 – х(х - 2) при х = - 1,2
9). Упростить выражение и найти его значение
2(3х + 1)2 при х = - 3
10).
в) Решить уравнения, применив ФСУ.
1). (6а - 1)(6а + 1) = 4а(9а + 2) – 1
2). (2х + 1)2 – 4х2 = 9 3). (2х - 3)2 = 9 + 4(х - 3)(х + 3)
4). (х - 5)2 = 5х2 – (2х - 1)(2х + 1)
5). (3х + 2)(3х - 2) – 32 = 9 (х - 2)2
6). (2х - 1)(2х + 1) – 4(х + 5)2 = 19
7). (3х + 2)(3х - 2) – 32 = 9 (х - 2)2
8). (6а - 1)(6а + 1) = 4а(9а + 2) – 1
9). (3х - 1)2 – 9х2 = 10
10). (2х + 1)2 – 3(х - 5)2 = (х + 3)(х - 3)
Зачётная работа №3. Функции
-
Найдите значение выражения
Заполните таблицу, вычислив значение выражения
| а | 5 | -2 | 4 | 1 | 6 |
| в | -3 | 3 | 0 | -1 | 4 |
| с | 4 | 0 | -5 | 7 | -2 |
| х | 2 | 3 | -1 | -2 | -3 |
| а – 2в | | | | | |
| с – 2са | | | | | |
| ав – 3с | | | | | |
| ах + вх + с | | | | | |
-
Найти значение функции.
Задание: вычислить значения заданной функции и заполнить таблицу.
1). у = 6х – 5
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| у | | | | | | | | | | |
2). у = 3х + 2
| х | -4 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| у | | | | | | | | | | |
