Ответы на вопросы экзамена АлГеМ

1. 
   Матрицы и их виды:
   

- Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы. Матрица порядка m × n записывается в форме:


Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j- номер столбца.


Определение: Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой:



Определение: Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом:

 

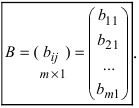
Определение: Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.

Определение: Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы - на соответствующие строки.

Определение: Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной:


Определение: Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали, называется диагональной:

---

 

Определение: Единичной матрицей называется диагональная матрица, у которой на главной диагонали все элементы равны единице, а остальные элементы равны нулю:

2. 
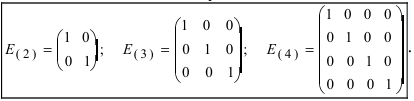
   Операции над матрицами и их свойства:
   

- Умножение матрицы на число

Произведением матрицы А на число  называется матрица   элементы которой   для 

Например, если  , то 

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например:
 

В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е. 

- Сложение матриц

Суммой двух матриц А и В одинакового размера  называется матрица   , элементы которой   для  (т.е. матрицы складываются поэлементно).

Например
 
В частном случае A + 0 = A.

- Вычитание матриц

---

Разность двух матриц одинакового размера определяется через предыдущие операции: 

- Умножение матриц

Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц   называется такая матрица , каждый элемент которой   равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В:

- Возведение в степень

Целой положительной степенью   квадратной матрицы   называется произведение   матриц, равных  , т.е.


Заметим, что операция возведения в степень определяется только для квадратных матриц.

По определению полагают   Нетрудно показать, что 

Пример №4

Найти   , где
 

Решение:


Обращаем внимание на то, что из равенства 

---

 еще не следует, что матрица   

- Транспонирование матрицы

Транспонирование матрицы— переход от матрицы   к матрице  , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица  называется транспонированной относительно матрицы  :

   

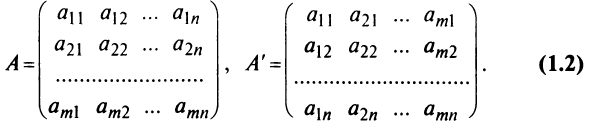
Из определения следует, что если матрица   имеет размер   , то транспонированная матрица   имеет размер  .

Например,
 
В литературе встречаются и другие обозначения транспонированной матрицы, например,  .

Свойства операции транспонирования:

3. 
   Определители и их свойства. Способы вычисления определителей.
   

- Необходимость введения определителя — числа, характеризующего квадратную матрицу  , — тесно связана с решением систем линейных уравнений (см. гл. 2). Определитель матрицы 

---

обозначается   или 

Определителем матрицы первого порядка  , или определителем первого порядка, называется элемент   :
 

Например, пусть   тогда 

Определителем матрицы второго порядка  , или определителем второго порядка, называется число, которое вычисляется по формуле:


Произведения а  и  называются членами определителя второго порядка.

Например, пусть   тогда

Пусть дана квадратная матрица третьего порядка:
   
Определителем матрицы третьего порядка  , или определителем третьего порядка, называется число, которое вычисляется по формуле:

---

Смотрите также файлы

• Задание для выполнения контрольной работы по дисциплине Гибкие оптические сети.pdf

• Учебнометодический комплекс по дисциплине Дискретная математика Основная образовательная программа 010800 Механика и математическое моделирование.pdf

• Реферат по информатике Программное обеспечение компьютера.doc

• терапия ВСЕ ТЕСТЫ.doc

• Udachi_na_ekzamene_33.docx