Файл: Исследование нестационарной теплопроводности в диэлектрической среде.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, где
D – коэффициент тепловой диффузии
Процесс передачи энергии в форме теплоты подчиняется закону теплопроводности Фурье:
, где 
– коэффициент теплопроводности
Внутреннее трение подчиняется закону Ньютона:
, где
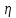– коэффициент внутреннего трения.
2.
Теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов). Другими словами, это способность материала проводить тепло.
Для количественной оценки теплопроводности существует коэффициент теплопроводности. Чем больше значение коэффициента теплопроводности, тем лучше он проводит тепло.
Коэффициент теплопроводности определяется уравнением Фурье и численно равен плотности теплового потока, проходящего через изотермическую поверхность при единичном температурном градиенте:
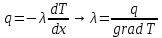
3.
Длина свободного пробега молекулы — это среднее расстояние λ, которое пролетает частица за время между двумя последовательными столкновениями.
В кинетической теории вводится понятие средней длины свободного пробега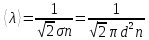
, где 
– эффективный диаметр молекулы,
n – концентрация молекул
Обработка результатов
1. Вычислите приращение температуры среды относительно исходной температуры
T(x; t) = T(x; t) T(x; 0)
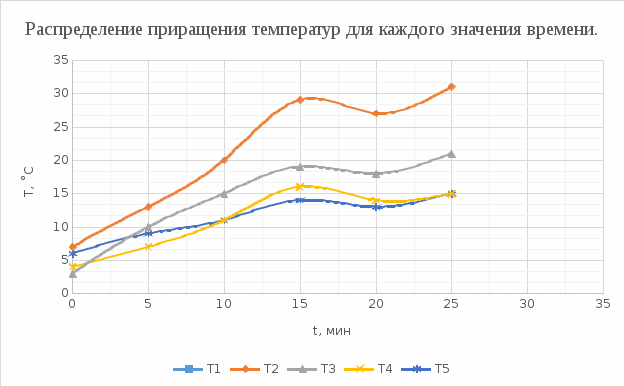
2. Построить графики распределения приращения температуры в координатах (x, T) для каждого значения времени tj
3.
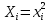и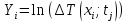 
. Найти коэффициенты линейных зависимостей Y1=a1X+b1, Y2=a2X+b2
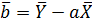
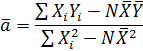
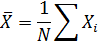
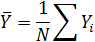
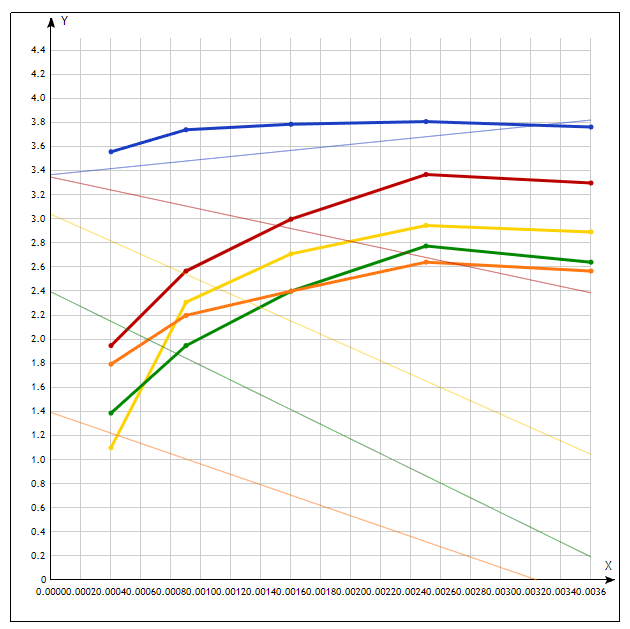
4. Построить графики распределения температуры в приведенных координатах (X, Y) для каждого значения времени tj
5. Введите обозначения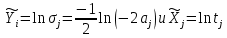
. Используя МНК, найдите по набору 
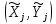коэффициенты 
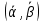линейной зависимости 
Коэффициенты:
, 
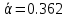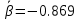
6. Сопоставьте найденное по МНК значение со значением 1/2
Полученное значение
< 1/2 => теоретическая зависимость среднеквадратичной ширины распределения температуры от времени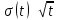 
выполняется.
7. Найти значение коэффициента диффузии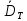
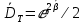= 0.088
Вывод: в ходе работы мной была исследована теплопроводность в диэлектрической среде. Был найден коэффициент диффузии и исследована зависимость среднеквадратичной ширины распределения температуры от времени.
D – коэффициент тепловой диффузии
Процесс передачи энергии в форме теплоты подчиняется закону теплопроводности Фурье:
, где – коэффициент теплопроводностиВнутреннее трение подчиняется закону Ньютона:
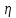, где – коэффициент внутреннего трения.2.
Теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов). Другими словами, это способность материала проводить тепло.
Для количественной оценки теплопроводности существует коэффициент теплопроводности. Чем больше значение коэффициента теплопроводности, тем лучше он проводит тепло.
Коэффициент теплопроводности определяется уравнением Фурье и численно равен плотности теплового потока, проходящего через изотермическую поверхность при единичном температурном градиенте:
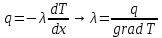
3.
Длина свободного пробега молекулы — это среднее расстояние λ, которое пролетает частица за время между двумя последовательными столкновениями.
В кинетической теории вводится понятие средней длины свободного пробега
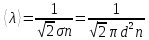, где – эффективный диаметр молекулы,n – концентрация молекул
Обработка результатов
1. Вычислите приращение температуры среды относительно исходной температуры
T(x; t) = T(x; t) T(x; 0)
| t, мин | ΔT1 | ΔT2 | ΔT3 | ΔT4 | ΔT5 |
| 5 | 35 | 7 | 3 | 4 | 6 |
| 10 | 42 | 13 | 10 | 7 | 9 |
| 15 | 44 | 20 | 15 | 11 | 11 |
| 20 | 45 | 29 | 19 | 16 | 14 |
| 25 | 43 | 27 | 18 | 14 | 13 |
| 30 | 50 | 31 | 21 | 15 | 15 |
2. Построить графики распределения приращения температуры в координатах (x, T) для каждого значения времени tj
3.
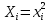и 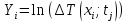. Найти коэффициенты линейных зависимостей Y1=a1X+b1, Y2=a2X+b2 | Xi | Yi1 | Yi2 | Yi3 | Yi4 | Yi5 |
| 0,0004 | 3,555 | 1,946 | 1,098 | 1,386 | 1,792 |
| 0,0009 | 3,738 | 2,565 | 2,306 | 1,946 | 2,197 |
| 0,0016 | 3,784 | 2,996 | 2,708 | 2,398 | 2,398 |
| 0,0025 | 3,806 | 3,367 | 2,944 | 2,773 | 2,639 |
| 0,0036 | 3,761 | 3,296 | 2,890 | 2,639 | 2,565 |
 |  |
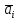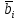| 126,049 | 3,365 |
| -266,900 | 3,345 |
| -553,507 | 3,036 |
| -611,187 | 2,392 |
| -429,311 | 1,391 |
4. Построить графики распределения температуры в приведенных координатах (X, Y) для каждого значения времени tj
5. Введите обозначения
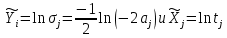. Используя МНК, найдите по набору 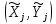коэффициенты 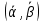линейной зависимости  |  |
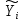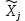| -3,107 | 5,704 |
| -2,872 | 6,397 |
| -3,343 | 6,802 |
| -3,538 | 7,090 |
| -3,576 | 7,313 |
Коэффициенты:
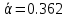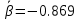
, 6. Сопоставьте найденное по МНК значение со значением 1/2
Полученное значение
< 1/2 => теоретическая зависимость среднеквадратичной ширины распределения температуры от времени 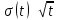выполняется.7. Найти значение коэффициента диффузии
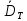
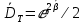= 0.088Вывод: в ходе работы мной была исследована теплопроводность в диэлектрической среде. Был найден коэффициент диффузии и исследована зависимость среднеквадратичной ширины распределения температуры от времени.