Глава 5

Тема: “Движение (перемещение) фигуры. Параллельный перенос.”

Движение фигуры F- Преобразование фигуры F,сохраняющее расстояние между точками.

Опр- Две фигуры называют равными ,если существует движение , при котором одна из данных фигур является образом другой.

Теорема 17.1 – Параллельный перенос является движением

Параллельный перенос - это частный случай движения, т.е. отображение плоскости на себя, при котором сохраняются расстояния.

Доказательство:

Дано: точки Еи К отображаются в точки Е₁и К₁ при параллельном переносе на  .

Доказать: параллельный перенос - движение.

Доказательство:

1 случай

Точки Еи К не лежат на одной прямой параллельной вектору  .



По условию точки Еи К отображаются в точки Е₁и К₁ соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса   и  , поэтому  , следовательно,   и  , значит, ЕЕ₁ КК₁ (т.к. точки Еи К не лежат на одной прямой параллельной вектору  ) и ЕЕ₁= КК₁. Следовательно, по признаку параллелограмма четырехугольник ЕЕ₁К₁К - параллелограмм, поэтому по свойству параллелограмма ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.

2 случай

Точки Еи К лежат на одной прямой параллельной вектору  .



По условию точки Еи К отображаются в точки Е₁и К₁ соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса   и  , поэтому  , следовательно,  , значит, ЕЕ₁

---

 = КК₁.  (1)

ЕК = КК₁ + ЕК₁, Е₁К₁= ЕЕ₁ + ЕК₁, тогда, учитывая (1), получим: ЕК = Е₁К₁, т.е. расстояние между точками Е и К равно расстоянию между точками Е₁ и К₁. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.

Следствие- Если фигура F- образ фигуры F при параллельном переносе ,то F1=F. (Используют при создание обоев, тканей и т.д.)



Задача 146.

a)

Треугольник ΔABC

A  A₁:

= 

 

B  B₁:

= 

 

C  C₁:

= 

б)

Треугольник ΔABC

A  A₁:  = 

 

B  B₁:

= 

 

C  C₁:

= 

Задача 147.

Дано:

треугольник ΔABC

AB = BC

точка D лежит на AC: D AC

точка C лежит на AD: C AD

BC  B₁D

 

а) Построить: B₁D

б) Доказать: ABB₁D – равнобедренная трапеция

 

а)

Построение:

1) От точки B проведем прямую a, параллельную вектору  : a || 

2) Точка B переводится движением в точку B₁

= 

3) Проведем прямую B₁D, параллельную отрезку BC:

B₁D || BC 

б)

Доказательство:

Рассмотрим четырехугольник BB₁DC.

Т.к. основания BB₁ || CD и боковые стороны BC || BD параллельны, то BB₁DC – параллелограмм (по определению)

По свойству параллелограмма:

основания BB₁ = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B₁D

Т.к. BB₁ || AD параллельны и AB   B₁D не параллельны, следовательно, ABB₁D – трапеция (по определению).

Т.к. AB = B₁D, то ABB₁D – равнобедренная трапеция.

Источники:

1. 
   Учебник
   
2. 
   https://budu5.com/manual/chapter/3583
   
3. 
   https://www.petrovskov.ru/uchebniki/geometriya-9/parallelnyj-perenos-povorot-ploskosti-i-podobnye-treugolniki.html
   

Тема: “Осевая симметрия”

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой

---

Опр-Точки А и В называют относительно прямой l, если прямая l является серединным перпендикуляром отрезка АВ



Теорема 18.1 – Осевая симметрия является движением.

Доказательство:

Пусть A и B — две произвольные точки фигуры F.

При симметрии относительно прямой g фигуры F точка A переходит в точку A1, точка B — в точку B1. При этом AO=A1O, BO1=B1O1и прямая g перпендикулярна отрезкам AA1 и BB1.

Проведём отрезки AO1 и A1O1.

Прямоугольные треугольники AOO1 и A1OO1 равны по двум катетам, следовательно, AO1=A1O1 и ∠OAO1=∠OA1O1. Прямые AA1 и BB1 параллельны по признаку параллельности прямых (как прямые, перпендикулярные одной и той же прямой g). ∠BO1A=∠OAO1 (как внутренние накрест лежащие при AA1 ∥ BB1 и секущей AO1) ∠B1O1A1=∠OA1O1 (как внутренние накрест лежащие при AA1 ∥ BB1 и секущей A1O1)

Следовательно, ∠BO1A=∠B1O1A1.

В треугольниках BO1A и B1O1A1:

1) ∠BO1A=∠B1O1A1;

2) BO1=B1O1;

3) AO1=A1O1.

Следовательно, эти треугольники равны (по двум сторонам и углу между ними).Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1, то есть расстояние между точками сохраняется, а значит, преобразование симметрии относительно прямой есть движение.

Следствие – Если фигуры F и F1 симметричны относительной прямой , то F= F1.

Опр - Фигуру называют симметричной относительно прямой l , если для каждой точки данной фигуры точка , симметричная ей относительно прямая l , также принадлежит этой фигуре .

Симметрия относительно прямой — осевая

Симметрия относительно точки — центральная



Задачи:





Источники :

1. 
   Учебник
   
2. 
   https://skysmart.ru/articles/mathematic/osevaya-i-centralnaya-simmetriya
   
3. 
   https://www.treugolniki.ru/osevaya-simmetriya/
   

Тема : “ Центральная симметрия . Поворот.”

Центральная симметрия - одно из свойств определённой геометрической фигуры, при котором точке В соответствует некая точка В1, находящая в таком же пространственном положении относительно точки С. Точка С лежит на середине отрезка ВВ1. Точка С называется центром симметрии. Это определение соответствует курсу планиметрии.

---

Теорема 19.1 – Центральная симметрия является движением

Доказательство:

Пусть A и B — две произвольные точки фигуры F.

При симметрии относительно точки O фигуры F точка A переходит в точку A1, точка B — в точку B1.

Рассмотрим треугольники AOB и A1OB.

1) AO=OA1

2) BO=OB1 (так как A и A1, B и B1 — точки, симметричные относительно точки O)

3) ∠AOB=∠B1OA1 (как вертикальные)

Следовательно, треугольники AOB и A1OB равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1, то есть расстояние между точками сохраняется, а значит, преобразование симметрии относительно точки является движением.

Следствие - Если фигуры F и F1 симметричны относительной прямой , то F= F1.

Опр – Фигуру называют симметричной относительной точки О , если для каждой точки данной фигуры точка, симметричная ей относительно точки О , так же принадлежит этой фигуре.

Задача  . В какую точку перейдет точка   при центральной симметрии относительно точки  ? Найти координаты получившейся точки  .



Решение

Если точка   переходит в некоторую точку  , то   – середина  . Значит, координаты точки   есть полусумма координат   и  :







То есть точка   имеет координаты  .

Задача  . Докажите, что при центральной симметрии прямая, не проходящая через центр симметрии, перейдет в прямую, параллельную исходной.

Решение

Пусть  . Нужно доказать, что   (Рис. 10).

 

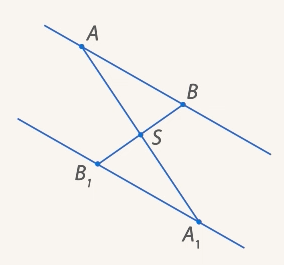
Рис. 10. Иллюстрация к условию

---

Точка   перешла в точку  , а точка   – в точку  . Образовалась прямая  , т.к. образом прямой при движении является прямая.

Распишем вектор  :   (коллинеарные векторы). Значит,  .

Источники:

1. 
   Учебник
   
2. 
   https://nauka.club/matematika/geometriya/tsentralnaya-simmetriya.html
   
3. 
   https://interneturok.ru/lesson/geometry/11-klass/bmetod-koordinat-v-prostranstveb/dvizheniya-tsentralnaya-i-osevaya-simmetrii
   

Теорема 19.2 – Поворот является движением.

Доказательство:

Если точки A, O и B не лежат на одной прямой.

Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.

Проведём отрезки AB и A1B1.

Рассмотрим треугольники AOB и A1OB1.

1) OA=OA1;

2) OB=OB1 (по определению поворота).

  

  

Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.

Если точки A, O и B лежат на одной прямой.

  

При повороте в направлении по часовой стрелке все рассуждения аналогичны.

Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.

Следствие – Если фигура F1- образ фигуры F при повороте , то F= F1.

Задача (аналогичная № 1167 из учебника Атанасян, см. список литературы)

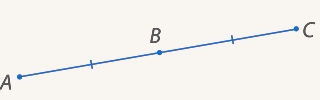
Постройте треугольник, который получается из данного треугольника ABC поворотом вокруг точки А на угол 60° против часовой стрелки (  ∆АВС).

Решение (Рис. 3).

 

 

 

 

 

 

 

 

 

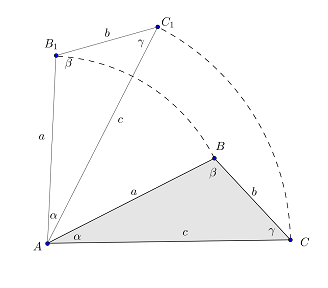
Рис. 3.

При повороте точка А перейдет в саму себя. Точки В и С перейдут в точки В

---

Смотрите также файлы

• Современные проблемы философии Содержание.docx

• .docx

• Лабораторная работа 4 Бурильная колонна. Цель работы изучение всех типов буровых труб. Дидактический материал.docx

• Техник системного администрирования.docx

• Моделирование, как метод изучения биологии.pptx