Файл: Движение (перемещение) фигуры. Параллельный перенос.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 и С1 соответственно. Углы треугольника и длины его сторон, в соответствии с общими свойствами движения, сохранятся (все обозначения сторон и углов даны на Рис. 3).
Построения при повороте крайне простые: при помощи циркуля построить дугу окружности радиусом, равным длине стороны треугольника (АС или АВ), с центром в точке А, далее при помощи транспортира отложить на дуге угол 60° и отметить точку-образ (В1 или С1). Соединив полученные точки-образы отрезками, можно получить искомый треугольник А1В1С1, являющийся образом треугольника АВС ( ∆АВС = ∆А1В1С1).
Задача (Атанасян, № 1168).
Точка О является точкой пересечения биссектрис равностороннего треугольника ABC. Докажите, что при повороте вокруг точки О на угол 120° треугольник ABC отображается на себя.
Решение.
Сделаем рисунок (Рис. 4).
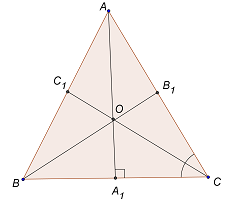
Рис. 4.
Точка О пересечения биссектрис правильного треугольника является центром этого треугольника. Следовательно, вершины треугольника при повороте вокруг точки О будут «отрисовывать» дуги окружности, описанной около ∆АВС. Легко показать, что ÐВОС = ÐСОА = ÐАОВ = 120°. Следовательно, при повороте , точка А перейдет в точку В, точка В перейдет в точку С и точка С перейдет в точку А (напомним, что угол поворота считается положительным, если поворот происходит против часовой стрелки). Таким образом, ∆АВС = ∆АВС .
Задача решена.
Задача. Дана прямая, на которой заданы точка О1 и точка О2 и даны точки А и В, лежащие по разные стороны от этой прямой. Причем имеют место равенства расстояний: О1А = О1В, О2А = О2В.
Доказать, что точки А и В симметричны относительно указанной прямой.
Решение (Рис. 5).
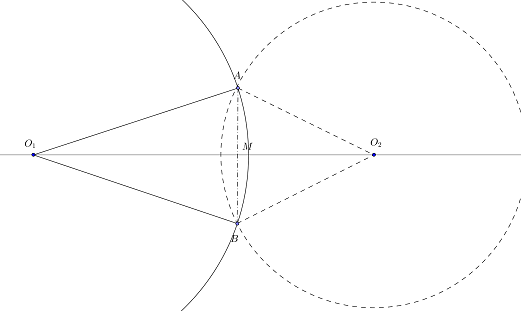
Рис. 5.
Для доказательства требуемого в задаче утверждения нам необходимо доказать, что АМ = МВ и АВ^ О1О2 .
Построим окружность радиусом О1А с центром в точке О1 и окружность радиусом О2А с центром в точке О2.
Рассмотрим некоторую осевую симметрию с осью О1О2. При таком отображении полуокружности, расположенные в верхней полуплоскости, перейдут в соответствующие полуокружности, расположенные в нижней полуплоскости относительно оси симметрии. При этом точка пересечения «верхних» полуокружностей – точка А – перейдет в точку пересечения «нижних» полуокружностей – точку В. То есть точка В симметрична точке А относительно рассматриваемой прямой. Задача решена.
В заключение разберем еще один простое применение понятий симметрии.
Дан параллелограмм ABCD.
Доказать, что точка пересечения его диагоналей является его центром симметрии.
Источники :
Тема: “Гомотетия. Подобие фигур”
Теорема 20.1- При гомотетии фигуры F с коэффициентом k все расстояния между ее точками изменяются в |k| раз, те если X и Y - произвольные точки фигуры F , а X1 и Y1- их соответствующие образы при гомотетии с коэффициентом k, то X1 и Y1=|k|XY
Если при гомотетии с коэффициентом k точки X и У переходят в точки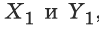
, то 
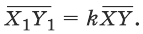
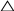
Следствие- Если треугольник А1 В1 С1 гомотетичен треугольнику АВС с коэффициентом гомотетии k , то А1В1С1
k АВС.
Свойства гомотетии :
- Центр гомотетии (O) - единственная двойная точка, и она превращается в себя; то есть не меняется.
- Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.
- Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.
- Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A'B ', так что AB будет параллельным A'B', а k будет:
- Гомотетические углы конгруэнтны; то есть они имеют одинаковую меру. Следовательно, изображение угла - это угол, имеющий одинаковую амплитуду..
С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:
- Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.
- Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).
- Если k = -1, гомотетия становится центральной симметрией (C); то есть вращение вокруг C будет происходить под углом 180или.
- Если k> 1, размер преобразованного рисунка будет больше размера исходного.
Источники:
Опр- Две фигуры называются подобными ,если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Теорема 20.2- Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Дано:
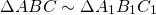
Доказать:
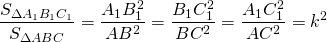
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
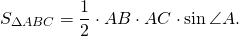
Аналогично,
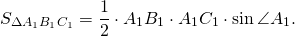
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
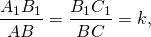
то есть
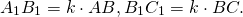
Теперь можем найти, как относятся площади подобных треугольников:
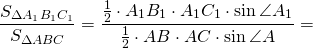
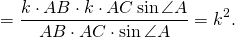
Так как
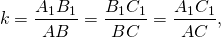
то
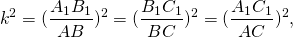
то есть
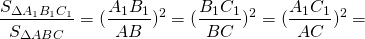
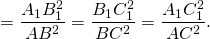
Что и требовалось доказать.
Задачи:
Задача 1.1. Построить образ треугольника при гомотетии с центром и коэффициентом .
Решение. Для построения образа
треугольника следует воспользоваться определением гомотетии. При гомотетии точка перейдет в такую точку , что
;
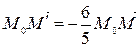точка − в такую точку , что
;
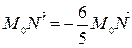а точка − в такую точку , что
.
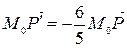Построим образ точки .
Так как , то точка лежит между точками и .
Так как
,
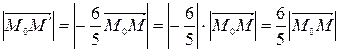то отрезок составляет отрезка . Учитывая все эти выводы, строим точку (рис. 22).
П
роводя аналогичные рассуждения для точек и , строим эти точки (рис. 22).
.
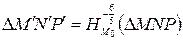Задача 1.2. Найти координаты образа и прообраза точки в гомотетии с центром и коэффициентом .
Решение. Воспользуемся аналитическим выражением гомотетии:
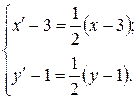
Чтобы найти координаты и образа точки , надо положить . Тогда
.
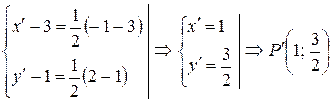Чтобы найти координаты прообраза точки (которая для является образом), можно записать формулы данной гомотетии в виде:
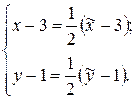
Полагая , находим и :
.
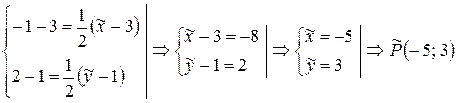Ответ: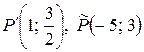
.
Задача 1.3. Через точку внешнего касания двух окружносте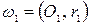й
и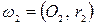 
неравных радиусов проведены две прямые и , 
, 
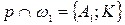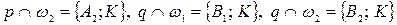. Доказать, что четырехугольник есть трапеция.
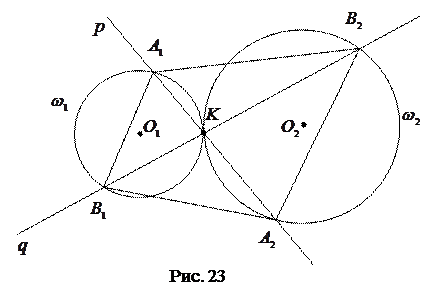
Решение. Чтобы доказать, что − трапеция, достаточно доказать, что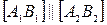
и (так как если бы , то четырехугольник был бы параллелограммом) (рис. 23).
Так как , то удобно воспользоваться гомотетией. Рассмотрим гомотетию с центром в точке и коэффициентом .
Так как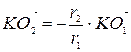
, то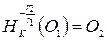 
, а так как отношение радиусов окружностей и равно , то 
.
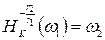Так как , то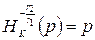
и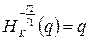 
(по свойству гомотетии).
, 
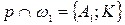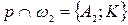. Тогда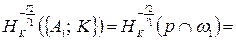 
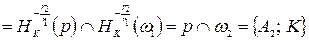. Отсюда и из того, что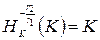 
Построения при повороте крайне простые: при помощи циркуля построить дугу окружности радиусом, равным длине стороны треугольника (АС или АВ), с центром в точке А, далее при помощи транспортира отложить на дуге угол 60° и отметить точку-образ (В1 или С1). Соединив полученные точки-образы отрезками, можно получить искомый треугольник А1В1С1, являющийся образом треугольника АВС ( ∆АВС = ∆А1В1С1).
Задача (Атанасян, № 1168).
Точка О является точкой пересечения биссектрис равностороннего треугольника ABC. Докажите, что при повороте вокруг точки О на угол 120° треугольник ABC отображается на себя.
Решение.
Сделаем рисунок (Рис. 4).
Рис. 4.
Точка О пересечения биссектрис правильного треугольника является центром этого треугольника. Следовательно, вершины треугольника при повороте вокруг точки О будут «отрисовывать» дуги окружности, описанной около ∆АВС. Легко показать, что ÐВОС = ÐСОА = ÐАОВ = 120°. Следовательно, при повороте , точка А перейдет в точку В, точка В перейдет в точку С и точка С перейдет в точку А (напомним, что угол поворота считается положительным, если поворот происходит против часовой стрелки). Таким образом, ∆АВС = ∆АВС .
Задача решена.
Задача. Дана прямая, на которой заданы точка О1 и точка О2 и даны точки А и В, лежащие по разные стороны от этой прямой. Причем имеют место равенства расстояний: О1А = О1В, О2А = О2В.
Доказать, что точки А и В симметричны относительно указанной прямой.
Решение (Рис. 5).
Рис. 5.
Для доказательства требуемого в задаче утверждения нам необходимо доказать, что АМ = МВ и АВ^ О1О2 .
Построим окружность радиусом О1А с центром в точке О1 и окружность радиусом О2А с центром в точке О2.
Рассмотрим некоторую осевую симметрию с осью О1О2. При таком отображении полуокружности, расположенные в верхней полуплоскости, перейдут в соответствующие полуокружности, расположенные в нижней полуплоскости относительно оси симметрии. При этом точка пересечения «верхних» полуокружностей – точка А – перейдет в точку пересечения «нижних» полуокружностей – точку В. То есть точка В симметрична точке А относительно рассматриваемой прямой. Задача решена.
В заключение разберем еще один простое применение понятий симметрии.
Дан параллелограмм ABCD.
Доказать, что точка пересечения его диагоналей является его центром симметрии.
Источники :
-
Учебник -
https://www.treugolniki.ru/povorot/ -
https://interneturok.ru/lesson/geometry/9-klass/dvizhenie/povorot-zadachi
Тема: “Гомотетия. Подобие фигур”
Теорема 20.1- При гомотетии фигуры F с коэффициентом k все расстояния между ее точками изменяются в |k| раз, те если X и Y - произвольные точки фигуры F , а X1 и Y1- их соответствующие образы при гомотетии с коэффициентом k, то X1 и Y1=|k|XY
Если при гомотетии с коэффициентом k точки X и У переходят в точки
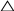
, то Следствие- Если треугольник А1 В1 С1 гомотетичен треугольнику АВС с коэффициентом гомотетии k , то А1В1С1
k АВС.Свойства гомотетии :
- Центр гомотетии (O) - единственная двойная точка, и она превращается в себя; то есть не меняется.
- Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.
- Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.
- Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A'B ', так что AB будет параллельным A'B', а k будет:
- Гомотетические углы конгруэнтны; то есть они имеют одинаковую меру. Следовательно, изображение угла - это угол, имеющий одинаковую амплитуду..
С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:
- Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.
- Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).
- Если k = -1, гомотетия становится центральной симметрией (C); то есть вращение вокруг C будет происходить под углом 180или.
- Если k> 1, размер преобразованного рисунка будет больше размера исходного.
Источники:
-
Учебник -
https://ru.thpanorama.com/articles/matemticas/homotecia-propiedades-tipos-y-ejemplos.html -
https://natalibrilenova.ru/preobrazovanie-podobiya/
Опр- Две фигуры называются подобными ,если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
| Подобие | = | Гомотетия | + | Движение |
Теорема 20.2- Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Дано: Доказать:
Площадь треугольника ABC может быть найдена, например, по двум сторонам и углу между ними:
Аналогично,
Так как углы подобных треугольников равны, а стороны — пропорциональны, то ∠A=∠A1,
то есть
Теперь можем найти, как относятся площади подобных треугольников:
Так как
то
то есть
Что и требовалось доказать.
Задачи:
Задача 1.1. Построить образ треугольника при гомотетии с центром и коэффициентом .
Решение. Для построения образа
треугольника следует воспользоваться определением гомотетии. При гомотетии точка перейдет в такую точку , что ;точка − в такую точку , что
;а точка − в такую точку , что
.Построим образ точки .
Так как , то точка лежит между точками и .
Так как
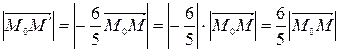,то отрезок составляет отрезка . Учитывая все эти выводы, строим точку (рис. 22).
П
роводя аналогичные рассуждения для точек и , строим эти точки (рис. 22).| | |
| | |
.Задача 1.2. Найти координаты образа и прообраза точки в гомотетии с центром и коэффициентом .
Решение. Воспользуемся аналитическим выражением гомотетии:
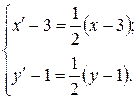
Чтобы найти координаты и образа точки , надо положить . Тогда
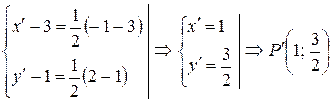.Чтобы найти координаты прообраза точки (которая для является образом), можно записать формулы данной гомотетии в виде:
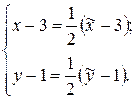
Полагая , находим и :
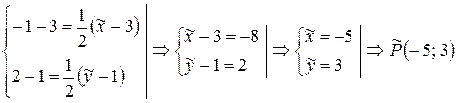.Ответ:
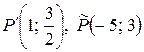.Задача 1.3. Через точку внешнего касания двух окружностей
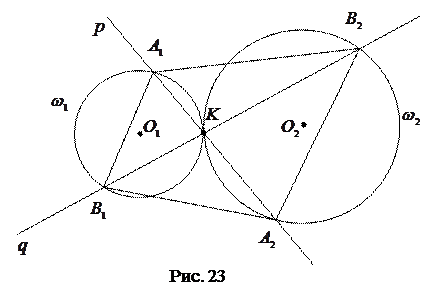
и неравных радиусов проведены две прямые и , , . Доказать, что четырехугольник есть трапеция. Решение. Чтобы доказать, что − трапеция, достаточно доказать, что
и (так как если бы , то четырехугольник был бы параллелограммом) (рис. 23).Так как , то удобно воспользоваться гомотетией. Рассмотрим гомотетию с центром в точке и коэффициентом .
Так как
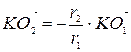, то , а так как отношение радиусов окружностей и равно , то .Так как , то
и (по свойству гомотетии). , . Тогда . Отсюда и из того, что