Задание 1

Даны комплексные числа: ;

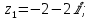
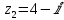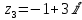
Найти z = 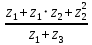в алгебраической форме.

Упростим дробное выражение, умножив и числитель, и знаменатель на сопряженное знаменателя:





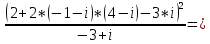
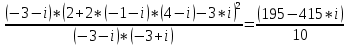
где



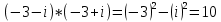
Упростим комплексное число



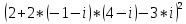
Возводим в квадрат по формуле



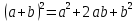
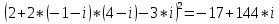
где





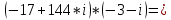
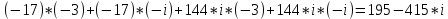
Ответ:

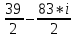
Задание 2

Дано число z = .

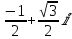а) найти тригонометрическую форму числа z;

Действительная часть числа х.



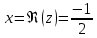
Мнимая часть числа y:



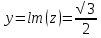
Модуль комплексного числа |z|



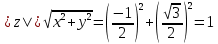
Поскольку 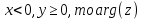находим как:

=



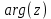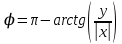
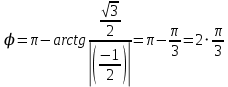
Таким образом, тригонометрическая форма комплексного числа z =

)

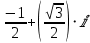
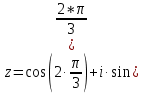б) найти z²⁰;

Действительная часть числа х.



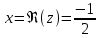
Мнимая часть числа у.

---

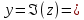
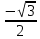
Модуль комплексного числа |z|

|z| = =

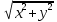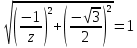
Поскольку 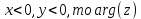находим как: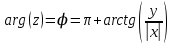





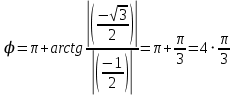
Таким образом, тригонометрическая форма комплексного числа



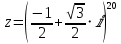
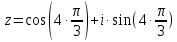
Находим показательную форму комплексного числа



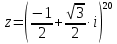
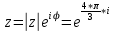
в) найти ;





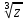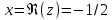
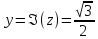
|z| =

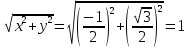
Поскольку 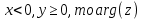находим как:

=



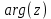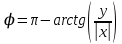
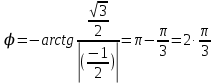
Таким образом, тригонометрическая форма комплексного числа



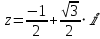
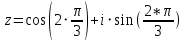
Извлекаем корни по формуле:









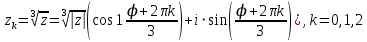
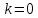
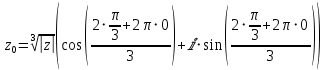
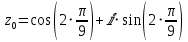
или



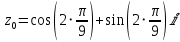
или









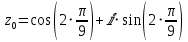
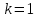
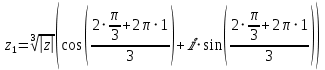
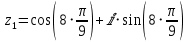
или

---

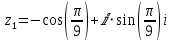
или









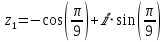
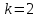
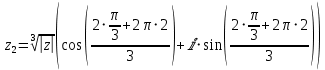
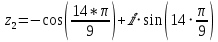
или



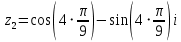
или



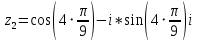
Задание 3

Вычислить определенные интегралы:

а)

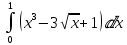
Применим линейность:

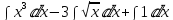
Далее вычисляем 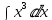, интеграл от степенной функции: 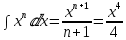(n = 3)

Теперь вычисляем: 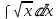(n = ) =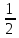

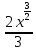
Далее вычисляем: 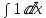= х

Подставим уже вычисленные интегралы:

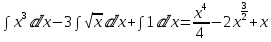
Ответ:

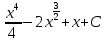
б)

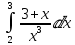
Используем свойство дистрибутивности:

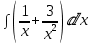
Применим линейность:

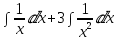
Теперь вычисляем:

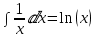
Далее вычисляем:

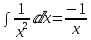
Подставим уже вычисленные интегралы:

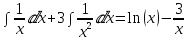
Ответ:

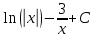
в)

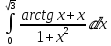
Используем свойство дистрибутивности:

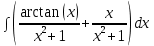
Применим линейность:

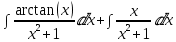
Далее вычисляем: =

---

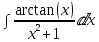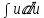
Интеграл от степенной функции:

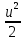
Обратная замена:

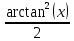
Теперь вычисляем: 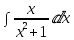= 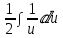, табличный интеграл =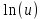

Подставим вычисленные интегралы: =

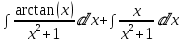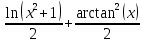
Задача решена: =

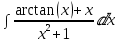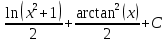
Упростим:

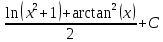
Ответ:

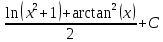
г) =

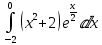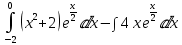
Теперь вычисляем:

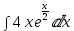
Применим линейность:

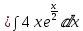
Следующим вычислим: =

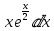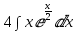
Теперь вычисляем: =

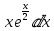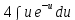
Следующим пунктом вычислим: =



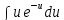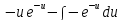
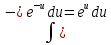
Интеграл от экспоненциальной функции: =

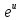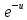
Подставим уже вычисленные интегралы:

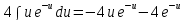
Обратная замена ;

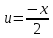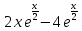
Подставим уже вычисленные интегралы:

---

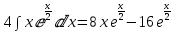
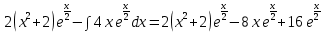
Задача решена:



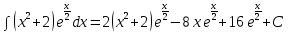
Упростим:



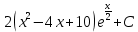
Ответ:

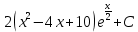
Задание 4

Решить дифференциальное уравнение с разделяющимися переменными:



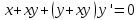
Для начала представим исходное дифференциальное уравнение в виде:



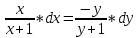
Интегрируя обе части, получаем:



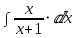
Степень числителя Р(х) больше или равна степени знаменателя Q(x), поэтому разделим полиномы:



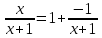
Интегрируя целую часть, получаем:



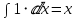
Интегрируя далее, получаем:



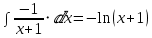
Отсюда ответ:





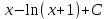
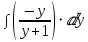
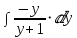
Степень числителя Р(у) больше или равна степени знаменателя Q(y) поэтому разделим полиномы.



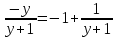
Интегрируя целую часть, получаем:

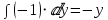
Интегрируя далее, получаем: =

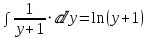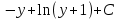
Ответ:

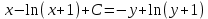
Задание 5

Решить однородное уравнение:

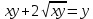
Дано уравнение:



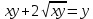
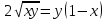
Возведем обе части уравнения во 2-ую степень:





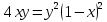
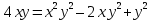
Теперь перенесем правую часть уравнения в левую часть со знаком минус:

---

Смотрите также файлы

• Геологогеофизический факультет.docx

• 2. в первой главе проанализированы.docx

• азастан тарихы 5 сынып Тас дуірі 1нса Жылы сйектері те кп табылан энеолиттік.doc

• Тесты бастау бизнес. Спасибо всем кто участвовал в проекте, но я вылажил эти ответы!.docx

• Сегодня один из главных объектов изучения науки о космосе планета Марс.docx