Файл: Задание 1 Даны комплексные числа Найти z в алгебраической форме. Упростим дробное выражение, умножив и числитель, и знаменатель на сопряженное знаменателя где Упростим комплексное число Возводим в квадрат по формуле где Ответ Задание 2.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Это уравнение вида:
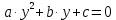
Это квадратное уравнение можно решить с помощью дискриминанта.
Корнями квадратного уравнения будут:
y1 =
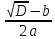
y2 =
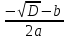
D =
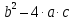 = это дискриминант. Т. к.
= это дискриминант. Т. к. 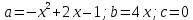
то,
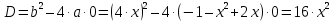
Уравнение имеет два корня:
y1 =
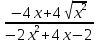
y2 =
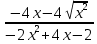
Задание 6
Решить линейное дифференциальное уравнение:
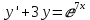
Дано уравнение:
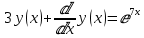
Это дифференциальное уравнение имеет вид:
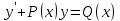
где
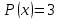
и
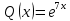
Линейное однородное дифференциальное уравнение 1-го порядка:
Для начала решаем линейное однородное уравнение:
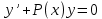
с разделяющимися переменными. Данное уравнение решается по шагам:
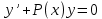 – из этого уравнения получаем
– из этого уравнения получаем 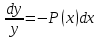
при y не равным 0
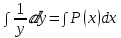
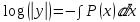
Или,
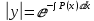
Поэтому,
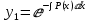
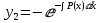
Из выражения видно, что надо найти интеграл:
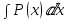
Т.к.
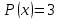
то
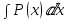
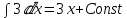
Значит решение однородного линейного уравнения:
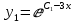
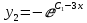
что соответствует решению с любой константой С, не равной нулю:
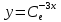
Таким образом мы нашли решение соответствующего однородного уравнения
Теперь надо решить наше неоднородное уравнение:
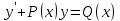
Используем метод вариации произвольной постоянной. Теперь считаем, что С – функция от х:
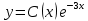
И подставим в наше исходное уравнение. Воспользовавшись правилами:
-
дифференцирования произведения; -
производной сложной функции,
находим, что
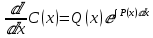
Подставим Q(x) и P(x) в это уравнение.
Получим простейшее дифференциальное уравнение для C(x):
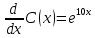
Значит, C(x)
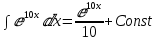
подставим C(x) в
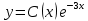
и получим окончательный ответ для y(x):
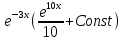
Ответ:
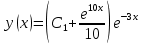
Задание 8
Решить дифференциальное уравнение:
a)
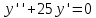
Это дифференциальное уравнение имеет вид:
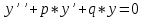
Где
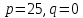
Это дифференциалньое уравнение 2-го порядка. Сначала мы найдем корни характеристического уравнения:
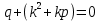
В нашем случае характеристическое уравнение будет иметь вид:
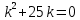
Корни этого уравнения:
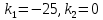
Т.к. характеристическое уравнение имеет два корня, то решение соответствующего дифференциального уравнения имеет вид:
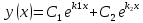
Получаем окончательный ответ:
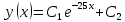
б)
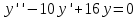
Это дифференциальное уравнение, которое имеет вид:
Где
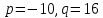
Линейное однородное дифференциальное уравнение 2-го порядка.
Сперва решаем линейное однородное уравнение:
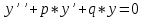
Ищем корни характеристического уравнения:
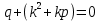
В нашем случае уравнение будет иметь вид:
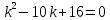
Корни этого уравнения:
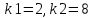
Т.к. характеристическое уравнение имеет два корня, то решение соотвтетсующего диффференциального уравнения имеет вид:
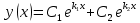
По итогу получаем:
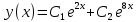
в)
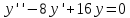
Это дифференциальное уравнение имеет вид:
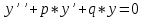
Где
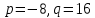
Это дифференциалньое уравнение 2-го порядка. Сначала мы найдем корни характеристического уравнения:
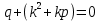
В нашем случае характеристическое уравнение будет иметь вид:
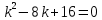
Корни этого уравнения:
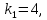
Т.к. характеристическое уравнение имеет один корень, то решение соответствующего дифференциального уравнения имеет вид:
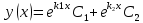
Подставляем: k1 = 4
Получаем окончательный ответ:
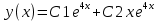
Задание 9
Решить дифференциальное уравнение:
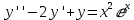
Это дифференциальное уравнение имеет вид:
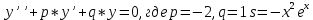
Линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
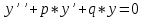
Сначала отыскиваем корни характеристического уравнения
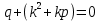
В нашем случае характеристическое уравнение будет иметь вид:
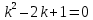
Простое квадратное уравнение. Корень этого уравнения:
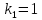
Т.к. корень уравнения один, то решения дифференциального уравнения имеет вид:
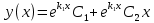
Подставляем:
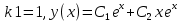
Теперь надо решить наше неоднородное уравнение
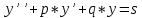
Используем метод вариации произвольной постоянной. Считаем, что С1 и С2 – это функции от х.
Общим решением будет:
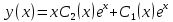
где С1(х) и С2(х), согласно методу вариации постоянных найдем из системы:
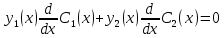
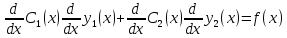
где
y1(x) и y2(x) – линейно независимые частные решения ЛОДУ,
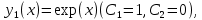
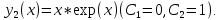
А свободный член
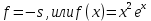
Значит, система примет вид:
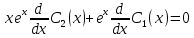
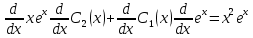
или
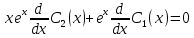
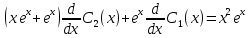
Решаем эту систему:
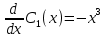
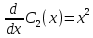 – это простые дифференциальные уравнения, теперь решаем их:
– это простые дифференциальные уравнения, теперь решаем их:С1(х) =
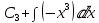
С2(х) =
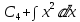
или
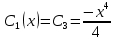
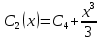
Подставляем найденные С1(х) и C2(x) в
y(x) = xC2(x)ex + C1(x)ex
Получаем окончательный ответ:
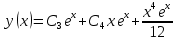
Задание 10
Решить дифференциальное уравнение:
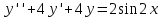
Это дифференциальное уравнение, которое имеет вид:
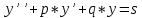
Где
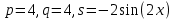
Это линейное неоднородное дифференциальное уравнение 2-го порядка.
Для начала решим подобное линейное однородное уравнение:
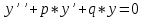
Ищем корни характеристического уравнения:
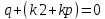
Уравнение в нашем случае будет иметь вид:
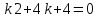 – это простое квадратное уравнение, корнем этого уравнения будет являться =
– это простое квадратное уравнение, корнем этого уравнения будет являться = 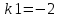
Т.к. корень характеристического уравнения один, то решение соответствующего дифференциального уравнения будет иметь вид:
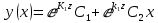
Теперь надо решить наше неоднородное уравнение:
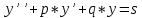
Используем метод вариации произвольной постоянной. Считаем, что С1 и С2 – это функции от х.
Общим решением будет: y(x) = xC2(x)e-2x + C1(x)e-2x
Где С1(х) и С2(х) согласно методу вариации постоянных найдем из системы:
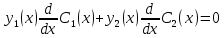
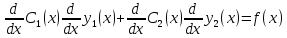
где y1(x) и y2(x) – линейно независимые частный решения ЛОДУ,
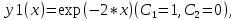
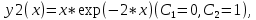
Свободный член
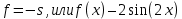
Значит система примет вид:
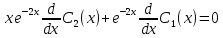
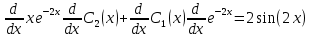
или