Файл: Решение а. Используем метод интегрирования частями б. Используем метод замены переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Найти неопределенный интеграл.
а).
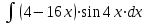 ; б).
; б). 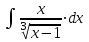 ; в).
; в). 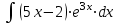 ; г).
; г). 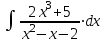 .
.Решение.
а). Используем метод интегрирования частями:
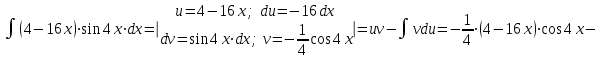
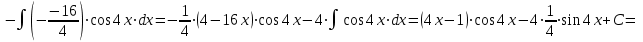
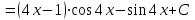 .
.б). Используем метод замены переменной:
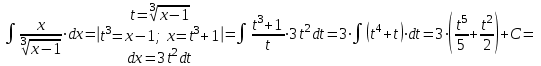
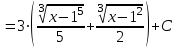 .
.в). Используем метод интегрирования частями:
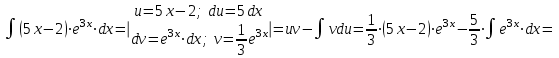
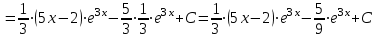 .
.г).
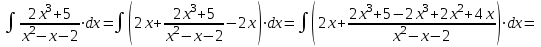
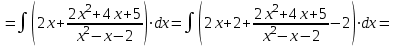
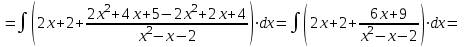
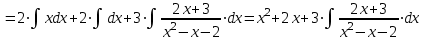 .
.Разложим последнее подынтегральное выражение на сумму простейших дробей, используя общий метод разложения.
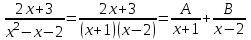 .
.Освобождаемся от знаменателей:
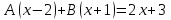 ;
; 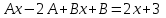 .
.Приравнивая коэффициенты при одинаковых степенях х левой и правой части, получим:
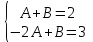 ;
; 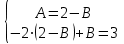 ;
; 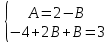 ;
; 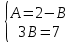 ;
; 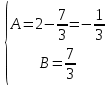 .
.Итак,
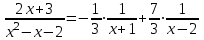 ;
;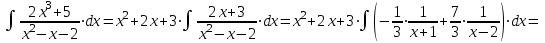
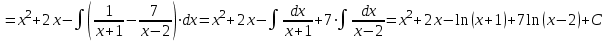
.
2. Вычислить по формулам Ньютона-Лейбница определённый интеграл:
а).
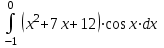 ; б).
; б). 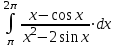 .
.Решение.
а). Найдем сначала соответствующий неопределённый интеграл, используя метод интегрирования частями:
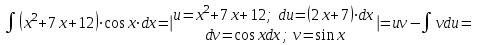
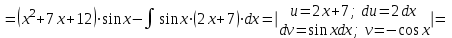
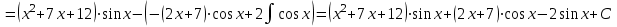
Используя формулу Ньютона-Лейбница, получим:
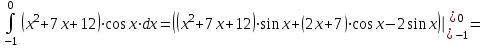
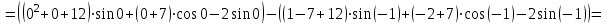
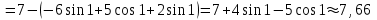 .
.б).
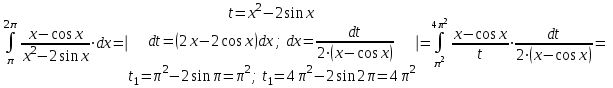
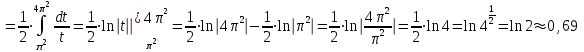 .
.3. Вычислить площадь фигуры, ограниченной линиями
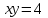 ,
, 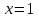 ,
, 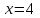 и
и 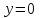
Решение.
Сделаем схематический чертеж указанной фигуры, ограниченной гиперболой
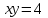 или
или 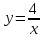 и прямыми
и прямыми 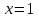 ,
, 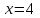 ,
, 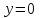 :
: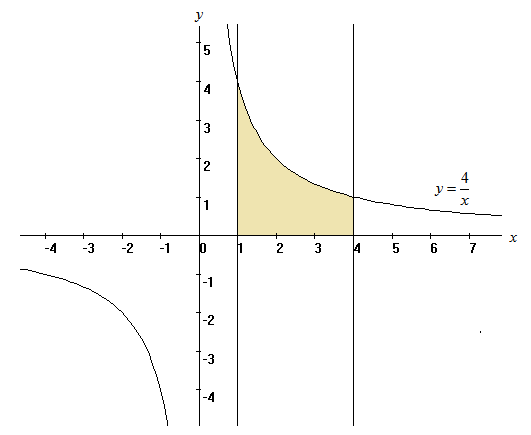
Площадь фигуры (закрашенной на чертеже) будем искать по соответствующей формуле через определенный интеграл, и именно
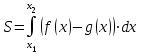 , где
, где 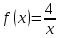 – функция, график которой ограничивает фигуру сверху,
– функция, график которой ограничивает фигуру сверху, 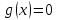 – функция, график которой ограничивает фигуру снизу.
– функция, график которой ограничивает фигуру снизу.Тогда, получим:
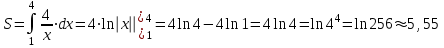
4. Найти полный дифференциал функции
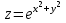 .
.Решение.
Находим частные производные первого порядка:
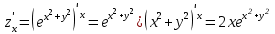 ;
;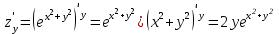 .
.По соответствующей формуле запишем полный дифференциал функции:
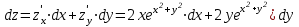 .
.5. Исследовать функцию
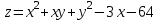 на экстремумы.
на экстремумы.Решение.
Сначала найдем все частные производные первого порядка:
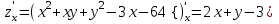 и
и 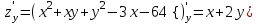 .
. Приравнивая их к нулю, получаем систему уравнений:
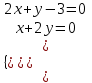 ;
; 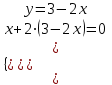 ;
; 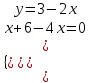 ;
; 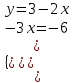 ;
; 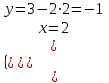 .
.Решению системы уравнений соответствует одна стационарная точка:
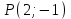 .
.Найдем частные производные второго порядка указанной функции:
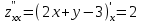 ;
; 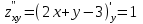 ;
; 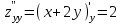 .
.Следовательно, вторые производные постоянные величины, т.е. в стационарной точке
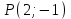 они равны
они равны 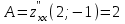 ,
, 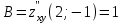 ,
, 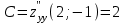 и вычисляем дискриминант
и вычисляем дискриминант 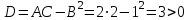 .
.Дискриминант имеет положительное значение, следовательно, экстремум в точке
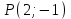 есть и, поскольку
есть и, поскольку 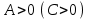 , то функция здесь имеет локальный минимум.
, то функция здесь имеет локальный минимум.Вычислим минимальное значение функции в точке
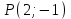 :
: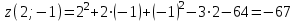
.
Следовательно, в точке
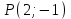 функция имеет минимум равный -67.
функция имеет минимум равный -67.6. Найти общее решение дифференциального уравнения
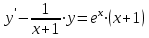 и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям 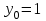 при
при 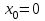 .
.Решение.
Для решения уравнения используем метод Бернулли.
Положим
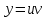 ; тогда
; тогда 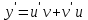 . Подставив выражения
. Подставив выражения 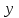 и
и 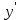 в исходное уравнение, получим:
в исходное уравнение, получим: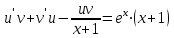 или
или 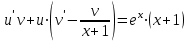 .
.Считая, что неизвестная функция
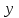 является произведением двух (также неизвестных) функций
является произведением двух (также неизвестных) функций 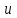 и
и 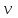 , мы тем самым можем одну из этих функций выбрать произвольно. Поэтому приравняем нулю коэффициент при
, мы тем самым можем одну из этих функций выбрать произвольно. Поэтому приравняем нулю коэффициент при 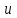 :
: 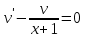 .
.Разделяя переменные в полученном уравнении, имеем:
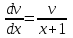 ;
; 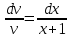 ;
;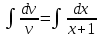 ;
; 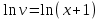 ;
; 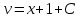 .
.Снова в виду произвольности в выборе
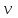 мы можем не учитывать произвольную постоянную
мы можем не учитывать произвольную постоянную 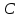 (точнее – можем приравнять её к нулю), т.е.
(точнее – можем приравнять её к нулю), т.е. 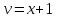
Найденное значение
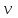 подставляем в уравнение
подставляем в уравнение 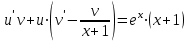 :
: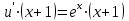
;
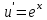 ;
;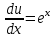 ;
; 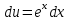 ;
; 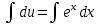 ;
; 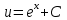 (здесь
(здесь 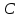 писать обязательно, иначе получится не общее, а частное решение).
писать обязательно, иначе получится не общее, а частное решение).Тогда, окончательно получим:
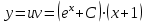 – общее решение уравнения.
– общее решение уравнения.Используя начальное условие, получим:
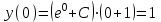 ;
; 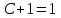 ;
; 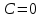
Следовательно,
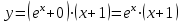 – частное решение.
– частное решение.7. а). Найти общее решение уравнения
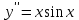 и частное решение, удовлетворяющее начальным условиям
и частное решение, удовлетворяющее начальным условиям 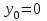
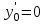 при
при 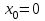 .
.б). Найти общее решение уравнения
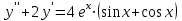 .
.Решение.
а). Имеем случай понижения порядка – отсутствует переменная у. Вводим замену
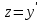 :
: 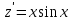 .
.Заменяя
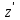 на
на 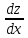 , получим:
, получим: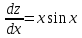 ;
; 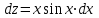 ;
;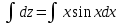 ;
;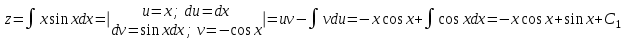 .
.Возвращаясь к замене, получим:
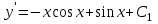 ;
; 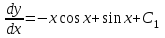 ;
; 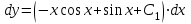 ;
;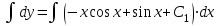 ;
;