Файл: Решение а. Используем метод интегрирования частями б. Используем метод замены переменной.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Решим отдельно интеграл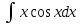
:
.
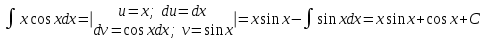Тогда, получим: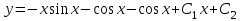
; 
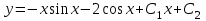– общее решение уравнения.
Используя начальное условие, находим постоянные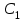
и 
:
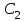1).
; 
; 
;
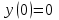
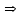
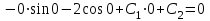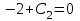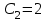2).
; 
.
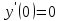
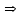
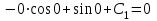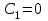Итак,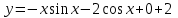
; 
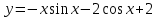– частное решение.
б). Составим характеристическое уравнение и найдем его корни:
; 
; 
, 
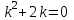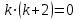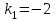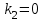– два неравных действительных корня.
Тогда, получим общее решение уравнения без правой части:
.
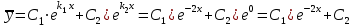Уравнение с правой частью имеет частное решение вида: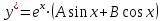
.
Находим коэффициенты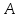
и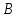 
, используя метод неопределенных коэффициентов.
;
.
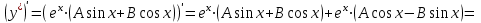
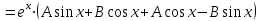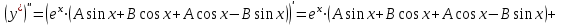
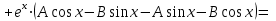
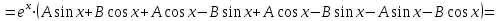
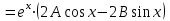Подставляя найденные значения в исходное уравнение, получим:
;
;
.
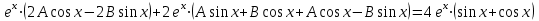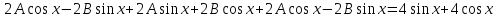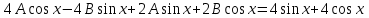Приравнивая одинаковые коэффициенты, получим:
; 
; 
; 
; 
;
.
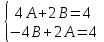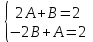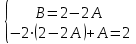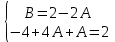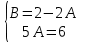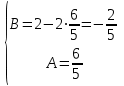Тогда, запишем частное решение: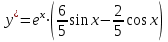
.
Полное решение заданного уравнения:
.
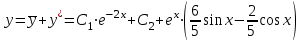8. Найти область сходимости ряда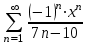
.
Решение.
Здесь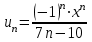
, 
.
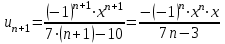Далее, используя признак Даламбера, ищем предел:
.
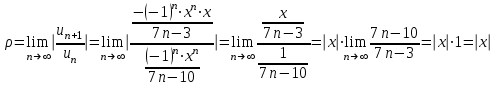И определяем, при каких значениях x этот предел будет меньше единицы, т.е. решаем неравенство:
; 
.
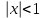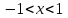Границы найденного интервала исследуем особо.
При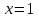
получим числовой знакочередующейся ряд 
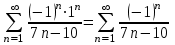, который сходится по признаку Лейбница: модуль общего члена стремится к 0 – 
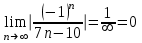и члены ряда убывают по абсолютному значению с увеличением порядкового номера.
При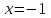
получим числовой положительный ряд 
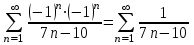. Используем предельный признак сравнения. Для этого сравним данный ряд с известным расходящимся гармоническим рядом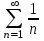 
.
Тогда, получим: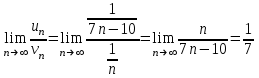
. Поскольку получили конечный ненулевой предел, то заданный ряд также расходится.
Следовательно, область сходимости есть –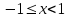
.
9. С точностью до 0,001 вычислить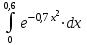
.
Решение.
Используя известное разложение функции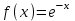
в степенной ряд: 
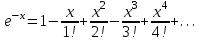разложим подынтегральную функцию в соответствующий ряд подставив вместо 
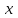выражение 
.
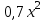Тогда, получим:
;
.
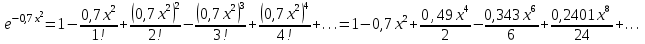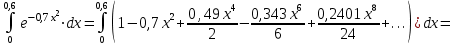
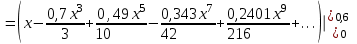Проводим соответствующие вычисления с заданной точностью:
, 
;
; 
;
; 
;
.
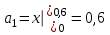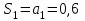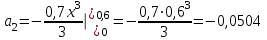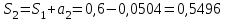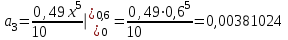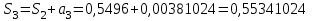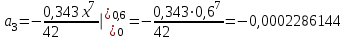Поскольку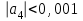
(заданная точность удовлетворяется), то 
.
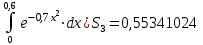Решим отдельно интеграл
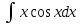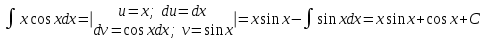: .Тогда, получим:
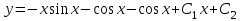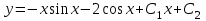; – общее решение уравнения.Используя начальное условие, находим постоянные
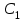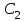и :1).
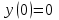
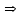
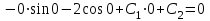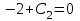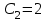; ; ;2).
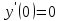
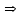
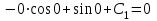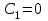; .Итак,
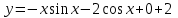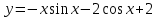; – частное решение.б). Составим характеристическое уравнение и найдем его корни:
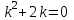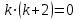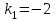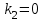; ; , – два неравных действительных корня.Тогда, получим общее решение уравнения без правой части:
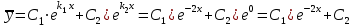.Уравнение с правой частью имеет частное решение вида:
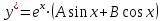.Находим коэффициенты
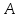и 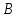, используя метод неопределенных коэффициентов. ;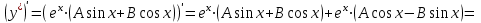
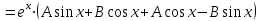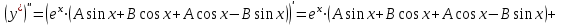
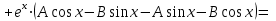
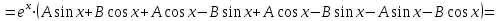
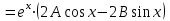.Подставляя найденные значения в исходное уравнение, получим:
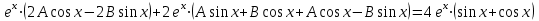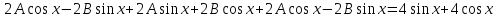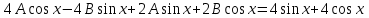; ; .Приравнивая одинаковые коэффициенты, получим:
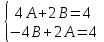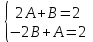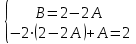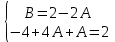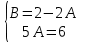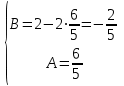; ; ; ; ; .Тогда, запишем частное решение:
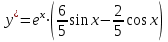.Полное решение заданного уравнения:
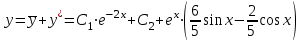.8. Найти область сходимости ряда
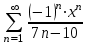.Решение.
Здесь
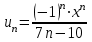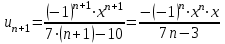, .Далее, используя признак Даламбера, ищем предел:
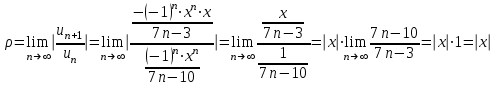.И определяем, при каких значениях x этот предел будет меньше единицы, т.е. решаем неравенство:
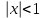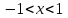; .Границы найденного интервала исследуем особо.
При
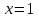получим числовой знакочередующейся ряд 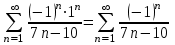, который сходится по признаку Лейбница: модуль общего члена стремится к 0 – 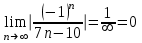и члены ряда убывают по абсолютному значению с увеличением порядкового номера.При
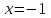получим числовой положительный ряд 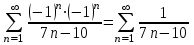. Используем предельный признак сравнения. Для этого сравним данный ряд с известным расходящимся гармоническим рядом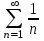
.
Тогда, получим:
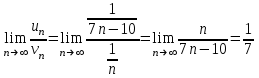. Поскольку получили конечный ненулевой предел, то заданный ряд также расходится.Следовательно, область сходимости есть –
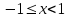.9. С точностью до 0,001 вычислить
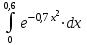.Решение.
Используя известное разложение функции
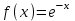в степенной ряд: 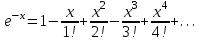разложим подынтегральную функцию в соответствующий ряд подставив вместо 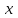выражение 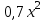.Тогда, получим:
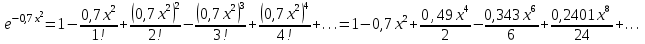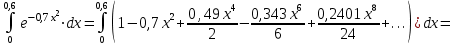
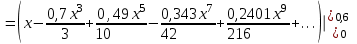; .Проводим соответствующие вычисления с заданной точностью:
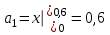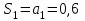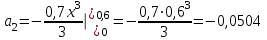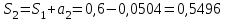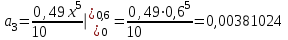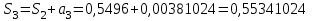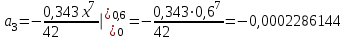, ; ; ; ; ; .Поскольку
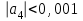(заданная точность удовлетворяется), то .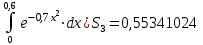