Файл: Основные определения.docx

1. 
   Основные определения.
   

Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.

Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.

Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.

Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.

Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).

Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила — действие приложена к связи, а реакция связи приложена к твердому телу.

Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.

Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.

Сила – это векторная величина, характеризующая механическое действие одного материального тела на другое.
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон.

Линия действия силы – это прямая, вдоль которой направлен вектор силы.

Сосредоточенная сила – сила, приложенная в одной точке.

Распределенные силы (распределенная нагрузка) – это силы, действующие на все точки объема, поверхности или длины тела.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м³ (Н/м², Н/м).

Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.

Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.

Система сил – это совокупность сил, действующих на механическую систему.

Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.

Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.

Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.

Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.

Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение:  .

Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.

Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
.

Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.
.

Момент силы – это величина, характеризующая вращающую способность силы.

Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение:  .
Под действием пары сил тело будет совершать вращательное движение.

Проекция силы на ось – это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси.

Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.

2. 
   Равнодействующая системы сил.
   

Равнодействующая системы - Векторная сумма всех сил, действующих на тело. При равномерном прямолинейном движении или в состоянии покоя равнодействующая сила равна нулю. 

3. 
   Главный вектор системы сил.
   

Главный вектор системы сил- вектор, равный геометрической сумме сил системы.

4. 
   Алгебраический момент силы относительно центра.
   

Момент силы относительно точки (или центра) — вращательный эффект силы, характеризующий вращение твердого тела вокруг некоторой точки под действием приложенной силы.

5. 
   Момент силы относительно оси.
   

Моментом силы относительно оси называют скалярную величину, равную моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью

6. 
   Пара сил, алгебраический моменты пары. Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны.Пара сил не имеет равнодействующей. Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил.
   

7. 
   Главный момент системы сил относительно центра.
   

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил

8. 
   Эквивалентные системы сил.
   

Если одну систему сил, действующих на данное свободное тело, можно заменить другой системой сил, не изменяя при этом покоя или его движения, в котором находится тело, то такие две системы сил называются эквивалентными.

9. 
   Связи и их реакции. Примеры.
   

Реакции гладкой поверхности и ребра

Реакции связей нити и стержня

Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня)

Реакции связей шарнирных опор

Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.

Реакции связи в заделках

Соединение стержня и втулки в плоскости

Реакции пространственных связей

Показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. 

10. 
    Равновесие системы сходящихся сил, равновесие плоской системы сил.
    

 для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны нулю.

Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма моментов этих сил относительно любой точки, находящейся в плоскости действия сил также была равна нулю.

11. 
    Равновесие сочлененных систем.
    

при равновесии системы тел каждое тело системы находится в равновесии, то задачи на равновесие системы сочлененных тел обычно решаются путем рассмотрения равновесия каждого тела в отдельности. При составлении уравнений равновесия какого-либо тела системы мы должны рассматривать другие, сочлененные с ним тела как связи и заменять их действие на рассматриваемое тело реакциями этих связей. 

12. 
    Теорема об эквивалентности двух систем сил.
    
13. 
    Две системы сил приложенных к свободному твердому телу, эквиваленты тогда и только тогда, когда, когда их главные векторы и главные моменты, относительно одного и того же произвольного центра, равны между собой.
    
14. 
    Приведение системы сил к центру.
    

Силу, приложенную к твердому телу, можно перенести параллельно самой себе в любую точку плоскости, если добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки.

15. 
    Теорема Вариньона.
    

момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.

16. 
    Распределенные нагрузки.
    

Распределенной нагрузкой называют внешние или внутренние усилия, которые приложены случайным образом или по заданному закону распределены по его определенной длине, площади или объему.

17. 
    Центр тяжести. Нахождение центра масс сложной фигуры.
    

Центр тяжести является точкой приложения равнодействующей силы тяжести, если силы тяжести отдельных его частей считать системой параллельных сил.

Метод симметрии( центр масс находится на оси симметрии)

Метод разбиения

Метод интегралов

Метод подвешивания

Метод отрицательных площадей

18. 
    Кинематика точки.
    

Кинема́тика то́чки — раздел кинематики, в котором изучается механическое движение материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без анализа вызывающих это движение причин; их рассматривает динамика, в частности, динамика точки.

19. 
    Три способа задания движения точки.
    

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

При координатном способе задания движения задаются координаты точки как функции времени.

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t).

20. 
    Определение скорости и ускорения точки для каждого способа задания движения точки.
    

Векторный способ:

Скорость точки равна первой производной от радиус-вектора точки по времени  . Вектор скорости   направлен по касательной к траектории в сторону движения точки.Ускорение точки равно первой производной от вектора скорости по времени или второй производной от радиус-вектора по времени  . Вектор ускорения   лежит в соприкасающейся плоскости траектории и направлен в сторону её вогнутости.Координатный способ:Для определения скорости точки   определяются проекции скорости на оси координат как первые производные от соответствующих координат точки по времени

 .

Проекции ускорения на оси координат равны первым производным от соответствующих проекций скорости по времени или вторым производным от соответствующих координат точки по времени

Естественный способ:Модуль скорости при естественном способе равен первой производной от дуговой координаты S по времени  .

Вектор ускорения   при естественном способе предстаёт как геометрическая сумма векторов касательного   и нормального   ускорений

21. 
    Касательное и нормальное ускорение. Радиус кривизны траектории.
    

Касательное ускорение характеризует изменение в данное мгновение вектора скорости по величине, а нормальное — по направлению

Радиус кривизны траектории-радиус окружности, которая сливается на бесконечно малом участке в данном месте с кривой

22. 
    Поступательное движение твердого тела. Поступательное движение< твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.
    
23. 
    Вращательное движение твердого тела. Вращательным движением называется движение, при котором все точки твердого тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения, причем эти окружности лежат в плоскостях, перпендикуляр-ных оси вращения. Угловые скорости всех точек тела одинаковы.
    
24. 
    Определение и уравнение вращательного движения твердого тела.
    

Вращательное движение твердого тела – это движение, при котором тело имеет как минимум две неподвижные точки Прямая, проходящая через эти точки, называется осью вращения.I*ԑ=M, I- момент инерции, ԑ-угловое ускорение, М- момент силы

25. 
    Угловая скорость и угловое ускорение вращающегося тела.
    

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени. Обозначение угловой скорости: ω (омега).

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела: Обозначение: ε (Эпсилон)

26. 
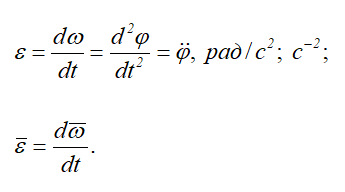
    Линейная скорость и линейное ускорение произвольной точки вращающегося тела.
    

Скорость точки вращающегося твердого тела определяется выражением

V=dS/dt=dφ∙R/dt=ωR    (2.9)

где ω — угловая скорость вращения твердого тела.

Скорость направлена по касательной к траектории, поэтому можно написать



Вектор скорости можно получить векторным произведением:

V=ω × r,
V=ω × r × sinα=ω×R.

Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений :

27. 
    Сложное движение тела. Скорости и ускорения точек в сложном движении. Ускорение Кориолиса. Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
    

Абсолютная скорость точки определяется как геометрическая сумма переносной и относительной скоростей:



Ускорение точки определяется как сума трех ускорений: переносного, относительного и кориолисова (поворотного):



Кориолисово ускорение — это векторная величина, равная   где   — угловая скорость неинерциальной системы отсчёта относительно инерциальной,   — скорость объекта в неинерциальной системе отсчёта.

28. 
    Плоско-параллельное движение тела. Мгновенный центр скоростей. Способы нахождения мгновенного центра скоростей
    

Плоскопараллельным/плоским движением ATT называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

В каждый момент времени при плоском движении тела, если  ,имеется единственная точка в плоскости его движения, скорость которой равна нулю.Эту точку называют мгновенным центром скоростей (МЦС). А)Известна скорость точки А и направление скорости точки В. МЦС находится на пересечении перпендикуляров к скоростям, проведённых в точках А и В . Б)Если скорости двух точек параллельны и с прямой, соединяющей точки образуют острые углы, то мгновенный центр скоростей не существует (находится в бесконечности). В этом случае скорости всех точек плоской фигуры равны, а угловая скорость равна нулю (рис. 16) .В)Если скорости двух точек не параллельны, то мгновенный центр скоростей лежит в точке пересечения перпендикуляров к ним. Г)Если скорости двух точек А и В плоской фигуры параллельны и с прямой, соединяющей эти точки, составляют прямые углы, то мгновенный центр скоростей Р находится как точка пересечения об щего перпендикуляра, восстановленного к скоростям в данных точках, и прямой, проходящей черезконцы векторов скоростей.

29. 
    Скорости и ускорения точек тела в плоском движении.
    

скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А

Vb=Va+Vab

Ускорение какой-либо точки тела при его плоском движении равно векторной сумме ускорения полюса и ускорения этой точки при вращательном движении тела вокруг полюса:

 

30. 
    Аксиомы динамики.
    

Закон 1(Закон инерции): Изолированная материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения пока и поскольку приложенные силы не заставят ее изменить это состояние.

Закон 2(Основной закон динамики): Производная по времени от количества движения МТ равна приложенной к ней силе. Закон 3(Закон равенства действия и противодействия): Две МТ действуют друг на друга с силами, которые равны по модулю и направлены в противоположные стороны по прямой, соединяющей эти МТ. Закон 4(Закон независимости действия сил): Если на МТ постоянной массы действует одновременно несколько сил, то каждая из этих сил действует независимо от других и сообщает МТ такое ускорение, которое она сообщила бы, действуя отдельно.

31. 
    Принцип Даламбера для точки.
    

Принцип Даламбера для материальной точки гласит: для движущейся точки в любой момент времени геометрическая сумма действующих на точку активных сил, реакций связи и сил инерции равна нулю. Другими словами, все внешние силы действующие на материальную точку при её движении всегда уравновешиваются силами инерции.

32. 
    Силы инерции.
    

 СИЛА ИНЕРЦИИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ F_i. Она возникает, когда тело движется по прямолинейной траектории.( F = ma)

 ЦЕНТРОБЕЖНАЯ СИЛА ИНЕРЦИИ F_i. возникает при вращении и направлена вдоль радиуса от центра вращения. (F_цб = mω²r)

СИЛА КОРИОЛИСА F_K. При совмещении двух видов движения: вращательного и поступательного – появляется еще одна сила, называемая силой Кориолиса (или кориолисовой силой)( F_K=2mυωsinα)

31 Момент инерции.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J .

33. 
    Механическая работа.
    

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути. А = FScosα

34. 
    Кинетическая энергия для точки и механической системы.
    

Кинетическая энергия материальной точки — скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости, т. е. Кинетическая энергия механической системы — арифметическая сумма кинетических энергий всех материальных точек этой системы.

35. 
    Теорема Кёнига.
    

кинетическая энергия системы в абсолютном движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс.

36. 
    Теорема об изменении кинетической энергии для механической системы.
    

 изменение кинетической энергии меха­нической системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних cuл, приложенных к системе, на этом перемещении:



36. Принцип Даламбера для механической системы.

для движущейся механической системы в любой момент времени геометрическая сумма главных векторов внешних сил, реакций связей, сил инерции равна нулю и геометрическая сумма главных моментов от внешних сил, реакций связей, сил инерции равна нулю.