ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Муниципальное бюджетное образовательное учреждение
«Основная школа №17 им. Т. Н. Хренникова»
Исследовательская работа
«Многочлены»
Выполнил:
Пойда Иван Олегович
Руководитель:
Васильева Татьяна Владимировна
Учитель математики
г. Елец-2023
Оглавление
I.Введение………………………………………………………………………..3-4
II. Многочлены…………………………………………………………………….4
-
Действия с многочленами. Степень многочлена………………….……4-7 -
Многочлен и его стандартный вид…………………………………….......8 -
Проверка многочлена на тождественность……………………….…….8-9
III. Заключение……………………………………………………………..….…10
IV. Список литературы…………………………………………………………..11
Введение
Актуальность исследовательской работы:
Математика помогает человеку в решении задач жизнедеятельности и производства. Любая данная ситуация рассматривается нами как математическая модель. Математической моделью может быть уравнение, алгебраическое выражение, график и прочее. Из курса алгебры для более глубокого изучения я выбрал тему: «Многочлены». Эта тема, в отличие от большинства тем школьной программы представляет собой математический аппарат для решения задач более широкого содержания, прежде всего решения уравнений и вопросов делимости целых и натуральных чисел.
Проблема исследовательской работы:
в школьной программе отсутствует теория деления многочленов, однако это знание может помочь при решении алгебраических уравнений.
Цель исследовательской работы:
изучить теорию делимости многочленов и области ее применения.
Объект исследования:
многочлены в курсе 8 класса.
Предмет исследования:
методы решения задач по данной теме.
Задачи исследовательской работы:
1.Необходимо изучить основные понятия, теоремы и алгоритмы теории многочленов.
2. Обобщить и систематизировать знания по данной теме.
3. Продемонстрировать применение основных методов решений на наглядных примерах.
4. Предоставить выводы по данной теме.
Гипотеза исследования:
алгоритм деления многочленов сокращает время на решение задач по разложению алгебраических выражений на множители.
Методы исследовательской работы:
моделирование, анкетирование, чтение учебной, литературы по проблеме исследования, поиск информации в глобальных компьютерных сетях.
Многочлены.
Общее понятие.
Многочленом называют сумму одночленов. Одночлены, входящие в эту сумму, называют членами многочлена. В математике, многочлены или полиномы от одной переменной — функции вида
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций. Многочлены, которые состоят из двух и трех членов, имеют специальные названия – двучлен и трехчлен соответственно. Так х+у – это двучлен(бином), а 2x3q−qx2+7b – трехчлен(трином), многочлен (полином). В своей работе я буду использовать многочлены стандартного вида первой степени, второй, третьей и четвёртой. (Степенью многочлена называют наибольшую из степеней входящих в него одночленов). В школе наиболее часто приходится работать с линейным двучленом a·x+b, где a и b– некоторые числа, а x – переменная, а также с квадратным трехчленом a·x2+b·x+c, где a, b и c – некоторые числа, а x – переменная. Вот примеры линейных двучленов: x+1 и 2x-5, а вот примеры квадратных трехчленов: x2+3x−5 и 3х2–2x–5.-
Действия с многочленами. Степень многочлена
Действия с многочленами.
Сложение (вычитание) многочленов.
Суммой (разностью) двух многочленов называется многочлен, коэффициенты которого являются суммой (разностью) коэффициентов при подобных членах этих многочленов. На практике для нахождения суммы и разности многочленов используют правила раскрытия скобок, перед которыми стоит знак плюс (знак минус).
Пример:(2x+3y) + (-5x+3y-4)=2x+3y-5x+3y-4=-3x+6y-4; (4x-5y)-(-x-4y)=4x-5y+x+4y=5x-y.
Умножение многочленов.
Чтобы умножить многочлен на одночлен, нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения. Чтобы умножить многочлен на многочлен, нужно умножить каждый член первого многочлена на каждый член второго многочлена полученные одночлены сложить.
Пример:(-5a)(4-b-a2)=-20a+5ab+5a3;
(2+b)(b2-4)=2b2-8+b3-4b.
Деление многочленов
В алгебре, деление многочленов столбиком — алгоритм деления многочлена f(x) на многочлен g(x), степень которого меньше или равна степени многочлена f(x). Алгоритм представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов f(x) и g(x),
, существуют единственные полиномы q(x) и r(x), такие что
,причем r(x) имеет более низкую степень, чем g(x). Целью алгоритма деления многочленов в столбик является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x).
Пример:
Покажем, что
Частное и остаток от деления могут быть найдены в ходе выполнения следующих шагов:
а). Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой
.
б). Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого
.
в). Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой
.
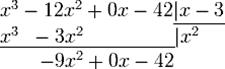
г). Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
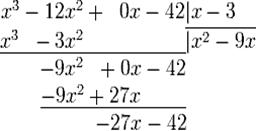
д). Повторяем шаг 4.
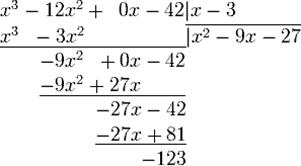
е). Конец алгоритма.
Таким образом, многочлен q(x) = x2 − 9x − 27 частное деления, а r(x) = − 123 — остаток.
Степень многочлена.
Многочлен может иметь степень — имеет на это полное право. Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов. Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду. Приводим многочлен к стандартному виду. Выбираем одночлен с наибольшей степенью.
Рассмотрим на примере:
Дан многочлен 6x + 4xy2 + x + xy2. Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:
6x и x — подобные слагаемые
4xy2 и xy2 — подобные слагаемые
Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.
Степень первого одночлена (7x) — 1.
Степень второго одночлена (5xy2) — 3.
Наибольшая из двух степеней — 3.
Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен третьей степени.
Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен третьей степени, поскольку оба многочлена равны друг другу. В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.
Пример: дан многочлен 6xx2 + 5xx2 − 3xx3 − 3x2x
Приведем его к стандартному виду: 6xx3 + 5xx2 − 3xx3 − 3x2x = 6x4 + 5x3 − 3x4 − 3x3 Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:
5x3 и −3x3 — подобные слагаемые.
6x4 и −3x4 — подобные слагаемые.
6x4 + 3x3 − 3x4 − 3x3 = 3x4 − 2x3
6xx3 + 5xx2 − 3xx3 − 3x2x — многочлен четвертой степени.
-
Многочлен и его стандартный вид
Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности. Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов. Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее. К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые. Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью. Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.
Дан красавец многочлен: 3x + 5xy2 + x − xy2
Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:
3x и x — подобные слагаемые.
5xy2 и −xy2 — подобные слагаемые.
Получаем многочлен вот такого вида: 3x + 5xy2 + x − xy2 = 4x + 4xy2.
Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.
-
Проверка многочлена на тождественность
Решение задачи с многочленами порой растягивается на несколько строк. Каждое следующее преобразование должно быть тождественно равно предыдущему. Если возникают сомнения в правильности своих действий, то можно подставить произвольные значения переменных в исходное и полученное выражение. Если исходное и полученное выражение будут равны одному и тому же значению, то можно быть уверенным, что задача была решена правильно.
Допустим, нам нужно вынести общий множитель за скобки в следующем многочлене:
2x + 4x2
В данном случае за скобки можно вынести общий множитель 2x
2x + 4x2 = 2x(1 + 2x)
Представим, что мы не уверены в таком решении. В этом случае нужно взять любое значение переменной x и подставить его сначала в исходное выражение 2x + 4x2, затем в полученное 2x(1 + 2x). Если в обоих случаях результат будет одинаковым, то это будет означать, что задача решена правильно. Возьмём произвольное значение x и подставим его в исходное выражение 2x + 4x2. Пусть x = 2. Тогда получим:
2x + 4x2 = 2 × 2 + 4 × 22 = 4 + 16 = 20
Теперь подставим значение 2 в преобразованное выражение 2x(1 + 2x)
2x(1 + 2x) = 2 × 2 × (1 + 2 × 2) = 4 × 5 = 20
То есть при x = 2 выражения 2x + 4x2 и 2x(1 + 2x) равны одному и тому же значению. Это значит, что задача была решена правильно. Тоже самое будет происходить и при других значениях переменных x. Например, проверим наше решение при x = 1
2x + 4x2 = 2 × 1 + 4 × 12 = 2 + 4 = 6
2x(1 + 2x) = 2 × 1 × (1 + 2 × 1) = 2 × 3 = 6
Заключение
Можно сделать вывод, что применение алгебраических правил настолько универсальны, что могут применяться не только в точных науках, но и в повседневной нашей жизни
Поэтому развитие науки, такой как алгебра, даёт нам огромную
помощь в нашей жизни и продвижении вперёд вместе научно-техническим прогрессом. И хочется выразить огромную благодарность всем учёным, математикам, чей вклад был внесён в развитие этой науки.
В этой работе я показал что такое многочлен, и объяснил как