Программа среднего профессионального образования

44.02.02 Преподавание в начальных классах

Дисциплина: Математика

Практическое занятие №1


Выполнил:

Обучающийся Кобзева Яна Александровна

Преподаватель:

Губарева Татьяна Викторовна

Задание № 1 Кобзева Я.А

Найти корень.

1. 
   1/3х^2=16 1/3
   

Решение:

Преобразуем число 16 1/3= 49/3

х^2=49/3:1/3=49/3*3/1=49

о ткуда имеем: х=+ 49=+ 7

меньше из корней равен -7

Ответ: -7

2. 
   х^2-17х+72=0
   

Решение: найдем корни квадратного уравнения через дискриминант:

D=b^2-4ac=289-288=1

Х1=-b+D/2a=17+1/2=9

Х2=-b-D/2a=17-1/2=8

Ответ:8

3. 
   х=6х-15/х-2
   

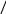
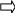
Р 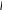ешение: уравнения имеет вид х-2= 0 х= 2

Перенесем знаменатель х-2 в левую часть получим

Х*(х-2)=6х-15

Х^2х-6х+15=0

Х^2-8х+15=0

Решаем квадратное уравнение: D=b^2-4ac=64-60=4

D=2

Х1=-b+D/2a=8+2/2=5

Х2=-8-D/2a=8-2/2=3

Больше из этих корней 5

Ответ: 5

4. 
   х+8/5х+7=х+8/7х+5
   

Р ешение:

5 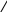х+7=0 х=-7/5

7х+5=0 х=-5/7

Так как числители х+8 в обеих частях уравнения равны, то общее равенство между левой и правой частями уравнения будут наблюдаться при:

---

Х+8=0 х=-8

5х+7=7х+5 х=1

Ответ:1

5. 
   15-2х=3
   

Решение:

15-2х=9

-2х=-6

Х=-6 : (-2)=3

Ответ:3

6. 
   Х-4=3
   

Решение:

Возводим в квадрат

Х-4=9

Х=9+4

Х=13

Ответ:13

Задание №2

Решение неравенства методом интервалов.

1.1/(х-2) (х-3) >0

Решение

( х-1) (х-2)/х-3 >0

- + - +

Х (1;2) (3;+бесконечность)

2. (х-3) (х-5) ( х+4) <0

Решение:

Х1=-4; х2=3; х3=5



Х (- бесконечность; -4) (3;5)

---

Смотрите также файлы

• Интенсивный курс Матрица, определитель и зачёт!.pdf

• Часть света, западная часть материка Евразия.docx

• Жолда жру ережелері Сабаты масаты.docx

• Сйлем мшелері трлаулы мшелер Сйлем рауа негіз болады.pptx

• Основы автоматизации технологических процессов нефтегазового производства.docx