ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И КОМПЬЮТЕРНОГО
МОДЕЛИРОВАНИЯ
КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Направление подготовки: 190700.62 «Технология транспортных процессов»
Профиль: «Организация и безопасность движения»
3 семестр
КУРГАН 2015
В третьем семестре выполняются контрольные работы №5 и №6. В контрольную работу №5 включены задачи из следующих разделов математики: «Кратные и криволинейные интегралы».
В контрольную работу №6 включены задачи из следующих разделов математики: «Элементы теории вероятностей и случайных процессов». «Элементы математической статистики».
Студент должен выполнять вариант, номер которого совпадает с последней цифрой его шифра (номера зачетной книжки), если последняя цифра 0, то решают задачи с ЖО, 20,30 и т.д.
Правила выполнения и оформления контрольных работ.
-
Каждая контрольная работа выполняется в отдельной тетради в клетку чернилами любого цвета, кроме красного.
2. В заголовке работы на обложке тетради должны быть указаны:
-
название дисциплины, -
номер контрольной работы, -
ФИО студента, -
номер группы, -
номер зачетной книжки студента.
-
В работу должны быть включены все задачи варианта. Контрольные работы, содержащие не все задачи, а также задачи не своего варианта не зачитываются. -
Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях.
5. Перед решением каждой задачи надо полностью записать ее условие.
6. Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как не зачтенной, так и зачтенной, студент должен исправить все отмеченные рецензентом ошибки и недочеты и выполнить все рекомендации рецензента. Если рецензент предлагает внести в решения задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. В случае незачета работы и отсутствия прямого указания рецензента о том, что студент может ограничиться представлением исправленных решений отдельных задач, вся работа должна быть выполнена заново. При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее.
ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
«МАТЕМАТИКА»
3 СЕМЕСТР
15. Кратные н криволинейные интегралы.
Двойной интеграл, его определение. Задачи, приводящие к понятию двойного интеграла. Вычисление двойного интеграла, его свойства. Изменение порядка интегрирования. Замена переменной в двойном интеграле. Якобиан. Двойной интеграл в полярных координатах. Приложения двойного интеграла к вычислению площадей плоских фигур в прямоугольных и полярных координатах. Вычисление объемов тел, статических моментов, моментов инерции и координат центра тяжести плоских фигур. Тройной интеграл. Его определение. Задачи, приводящие к понятию тройного интеграла. Механический смысл тройного интеграла. Свойства тройных интегралов. Замена переменных в тройном интеграле. Общая формула замены переменных. Якобиан. Цилиндрические и сферические координаты. Приложения тройных интегралов к вычислению объемов тел, статических моментов, моментов инерции, координат центра тяжести пространственных тел. Криволинейные интегралы по длине дуги (1-го рода), их свойства и вычисление в декартовых, полярных координатах, в параметрической форме. Механический смысл криволинейного интеграла 1-го рода. Приложения криволинейных интегралов 1-го рода, к вычислению длины дуги плоской кривой, статических моментов, моментов инерции и координат центра тяжести плоской дуги. Криволинейный интеграл
II-го рода (по координатам), его механический смысл, свойства и вычисление в
декартовых координатах, параметрической форме. Приложения криволинейного
интеграла II-го рода. Условие независимости криволинейного интеграла от пути
интегрирования. Интегралы от полных дифференциалов. Криволинейные интегралы по
замкнутому контуру. Формула Грина. Восстановление функции по ее полному
дифференциалу.
16. Элементы теории вероятностей и случайных процессов.
Алгебра событий. Частота событий, ей свойства. Статистическое и классическое
определение вероятности событий. Геометрическая вероятность. Комбинаторный метод
вычисление вероятностей. Теоремы сложения и умножения, следствия. Формула полной
вероятности и теорема гипотез (формула Байеса). Повторение испытаний. Схема
Бернулли. Формула Бернулли. Локальная и интегральная теоремы Лапласа. Производящая
функция. Понятие случайной величины. Дискретные и непрерывные случайные
величины. Закон распределения случайной величины. Функция распределения и её
свойства. Плотность распределения непрерывной случайной величины. Числовые
характеристики случайных величин. Законы биномиального распределения,
распределение Пуассона, равномерного распределения, показательного распределения.
Определения, условия возникновения, числовые характеристики. Нормальное
распределение: определение, числовые характеристики, влияние числовых характеристик
на форму кривой Гаусса. Вероятность попадания нормально распределенной случайной
величины в заданный интервал. Правило «трех сигм». Закон больших чисел. Неравенство
и теоремы Чебышева. Понятие случайного процесса (функции). Классификация
случайных процессов. Основные характеристики случайного процесса: математическое
ожидание и дисперсия. Корреляционная функция случайного процесса. Взаимная
корреляционная функция случайного процесса. Стационарные случайные процессы в
узком и широком смысле. Дифференцирование и интегрирование случайных процессов.
Спектральное разложение стационарного случайного процесса. Спектральная плотность
случайного процесса. Стационарный белый шум.
17. Элементы математической статистики.
Генеральная и выборочная совокупность. Статистическое распределение выборки.
Эмпирическая функция распределения и ее свойства. Полигон и гистограмма частот.
Точечные и интервальные оценки параметров распределения.Метод моментов и
максимального правдоподобия. Доверительные интервалы с заданной надежностью.
Статистические гипотезы. Критерии согласия, критические точки. Критерий «хи квадрат»
Пирсона. Проверка гипотезы о нормальном распределении вероятностей по данным
выборки. Элементы теории корреляционно-регрессионного анализа. Понятие
функциональной, стохастической и корреляционной зависимости. Выборочное
корреляционное отношение. Линейная корреляция. Обработка результатов наблюдений по
методу наименьших квадратов. Линейное уравнение регрессии.
Литература.
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. М.: Наука,
1970. Т. 1.
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах, М.: Высшая
школа. Ч. 1. 1980.
3. Запорожец Г.И. Руководство к решению задач по мат анализу. М.: Высшая школа, 1966.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической
статистике. М.: Высшая школа, 1970.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа,
1972.
6. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969.
КОНТРОЛЬНАЯ РАБОТА № 5
ВАРИАНТ 1
1. Вычислить двойной интеграл ∫∫(x2 + y)dxdyпо области D, ограниченной
D
линиями: у = х2, x = у2.
2. Вычислить площадь фигуры, ограниченной линиями:
у2=4x, x + y=3, y ≥ 0
3. Вычислить тройной интеграл ∫∫∫(2x2
+ 3у + z)dxdydz, если область V
v
задается неравенствами: 2
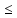х ≤3, -1 ≤ у ≤2, 0 ≤ z ≤4.4. Вычислить криволинейный интеграл ∫ (х2 + у2)dx + 2xydy, где L0А - дуга
LOA
кубической параболы у = х3 от точки O(0;0) до точки А(1;1).
ВАРИАНТ 2
1. Вычислить двойной интеграл ∫∫ xy2dxdyпо области D, ограниченной
D
линиями: у = х2,y=2x.
2. Вычислить площадь фигуры, ограниченной линиями; у = 6х2, х + у = 2, х≥0.
3. Вычислить тройной интеграл ∫∫∫x2yzdxdydz, если область V задается
V
неравенствами: −1 ≤ х ≤ 2, 0
≤ у ≤ 3, 2 ≤ z ≤ 3.
4. Вычислить криволинейный интеграл ∫2xydx − x2dy, где L0BА-
LOBA
ломаная ОВА: O(0;0), В(2;0), А(2;1).
ВАРИАНТ 3
1. Вычислить двойной интеграл ∫∫(x+ y)dxdyпо области D, ограниченной
D
линиями: у = х, х = у2.
2. Вычислить площадь фигуры, ограниченной линиями:у2 =х+ 2, х = 2.
3. Вычислить тройной интеграл ∫∫∫(x + y + 4z2)dxdydz, если область V задается
V
неравенствами: −1≤ х ≤1, 0≤y≤2, −1≤z ≤1.
4. Вычислить криволинейный интеграл ∫(x2