ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 21
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
−y2)dx+ xydy , где LАB-
LAB
отрезок прямой АВ: А(1;1), В(3;4).
ВАРИАНТ 4
1.Вычислить двойной интеграл ∫∫ x2ydxdyпо области D, ограниченной
D
линиями:у = 2 − х, у = х, х ≥ 0.
2. Вычислить площадь фигуры, ограниченной линиями: x = −2y2, x = 1−3y2, x ≤ 0, y≥ 0.
3. Вычислить тройной интеграл ∫∫∫(x2 + y2 + z2)dxdydz, если область V задается
V
неравенствами:0 ≤ х ≤ 3, −1 ≤ у ≤ 2, 0 ≤ z≤2.
4.Вычислить криволинейный интеграл ∫xydx + (y −x)dy + xydy, где LАB- дуга
LAB
кубической параболыу = х3 отточки А(0;0) до точки В(1;1).
ВАРИАНТ 5
1. Вычислить двойной интеграл ∫∫ (x3 −2y)dxdyпо области D, ограниченной
D
линиями:у = x2 −1, x≥ 0, y≤ 0.
2. Вычислить площадь фигуры, ограниченной линиями:у = х2 +1, x +y= 3.
3. Вычислить тройной интеграл∫∫∫x2y2zdxdydz, если область V задается
V
неравенствами: −1 ≤ x≤ 3, 0 ≤ у ≤ 2, − 2 ≤ z≤ 5.
4. Вычислить криволинейный интеграл ∫(x2+ y2)dx+(x +
y2)dy , где
LABC
LABC - ломаная ABC: А(1;2), В(3;2), С(3;5),
ВАРИАНТ 6
1. Вычислить двойной интеграл ∫∫ (y−x)dxdyпо области D, ограниченной
D
линиями:у = х2, х = у.
2. Вычислить площадь фигуры, ограниченной линиями: у2 = 4х, х2 = 4у.
3. Вычислить тройной интеграл ∫∫∫(x + y + z)dxdydz, если область V задается
V
задается неравенствами: 0 ≤ х ≤ 1, −l ≤ y≤ 0, l ≤ z≤ 2.
4. Вычислить криволинейный интеграл ∫xydx + (y −x)dy , где LOA- дуга
LOA
параболы у2 = xот точки O(0;0) до точки А(1;1).
ВАРИАНТ 7
1.Вычислить двойной интеграл ∫∫ (1+y)dxdyпо области D, ограниченной
D
линиями: у2 = х, 5у = х.
2.Вычислить площадь фигуры, ограниченной линиями: у = х2 + 2, х ≥ 0, х = 2, у = х.
3.Вычислить тройной интеграл ∫∫∫(2x − y2 −z)dxdydz, если область V задается
V
задается неравенствами: l ≤ x ≤ 5, 0 ≤ y ≤ 2, −l ≤ z ≤ 0.
4.Вычислить криволинейный интеграл ∫(xy-1)dx+ x2ydy , где LАB- дуга
LAB
параболы у2 = 4 − 4х от точки А(1;0) до точки В(0;2).
ВАРИАНТ 8
1.Вычислить двойной интеграл ∫∫ (x+y)dxdyпо области D, ограниченной
D
линиями: у = х2-1, у = −х2 +1.
2.Вычислить площадь фигуры, ограниченной линиями: у = х2, у = −х
.
3.Вычислить тройной интеграл ∫∫∫2xy2zdxdydz, если область V задается
V
неравенствами: 0 ≤ х ≤ 3, −2 ≤ у ≤ 0, 1 ≤ z ≤ 2.
4.Вычислить криволинейный интеграл ∫xydx + (y −x)dy , где LOA- дуга
LOA
параболы у= x2от точки O(0;0) до точки А(1;1).
ВАРИАНТ 9
1.Вычислить двойной интеграл ∫∫ x (y+1)dxdyпо области D, ограниченной
D
линиями: у = 5х, х = у, х = 3.
2.Вычислить площадь фигуры, ограниченной линиями: x= у2, x=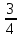
y2+1.
3.Вычислить тройной интеграл ∫∫∫5xyz2dxdydz, если область V задается
V
неравенствами: −1≤ х ≤ 0, 2 ≤ у ≤ 3 1≤ z ≤ 2.
4.Вычислить криволинейный интеграл ∫(xy−y2)dx+ xdy , где LOA- дуга
LOA
параболы у = х2 от точки O(0;0) до точки А(1 ;1).
ВАРИАНТ 10
1.Вычислить двойной интеграл ∫∫ (x+2)ydxdyпо области D, ограниченной
D
линиями: у = х, у =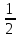
х, х = 2.
2.Вычислить площадь фигуры, ограниченной линиями: у = х2 +4х, у = х + 4.
3.Вычислить тройной интеграл ∫∫∫(x2+2y2 − z)dxdydz, если область V задается
V
неравенствами: 0 ≤ x≤ 1, 0 ≤ y≤ 3, −l ≤ z≤ 2.
4.Вычислить криволинейный интеграл ∫(xy − x
)dx+
x2dy , где LOA- дуга
LOA
параболы у2 = 4х от точки O(0;0) до точки А(1;2).
КОНТРОЛЬНАЯ РАБОТА № 6
ВАРИАНТ 1
1.На пяти карточках написаны цифры от 1 до 5. Опыт состоит в случайном выборе трех карточек и раскладывании их в порядке поступления в ряд слева направо. Найти вероятности следующих событий: а) появится число 123; б) появится число, не содержащее цифры 3.
2.На фабрике, изготовляющей болты, первая машина производит 25% всех изделий, вторая 35% и третья - 40%. Брак в их продукции составляет соответственно 5%, 4% и 2%. Найти вероятность того, что случайно выбранный болт окажется бракованным.
3.В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения случайной величины X - числа стандартных деталей среди отобранных. Найти математическое ожидание и дисперсию случайной величины X.
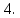Случайная величина X задана интегральной функцией распределения F(x):
F(x) =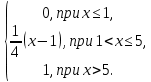
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4) вероятность попадания случайной величины X в интервал (2;3);
5) построить графики F(x) и f(x).
ВАРИАНТ 2
1.В ящике лежит 12 красных, 8 зелёных 10 синих шаров. Наудачу
вынимаются два шара. Найти вероятность того, что они разного цвета.
2.Два завода поставляют асфальтобетон одному ДСУ. Производительность
первого в два раза больше производительности второго завода. Первый завод
производит в среднем 60% асфальтобетона отличного качества, второй - 84%.
Наудачу взятая проба асфальтобетона, оказалась отличного качества. Найти
вероятность того, что этот бетон изготовлен на первом заводе.
3.В партии из 25 деталей имеется 6 бракованных. Наудачу отобраны три
детали. Составить закон распределения случайной величины
X - числа бракованных деталей среди отобранных. Найти математическое
ожидание и дисперсию случайной величины X.
4.Случайная величина X задана интегральной функцией распределения F(x):
F(x) =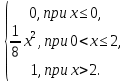
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4)вероятность попадания случайной величины X в интервал (0;1);\
5) построить графики F(x) и f(x).
ВАРИАНТ 3
1.На строительстве моста среди прочих машин используется 15
автогрейдеров и 10 бульдозеров. Необходимо выделить 5 машин на другой
объект. Какова вероятность того, что в их число попадут три автогрейдера и
два бульдозера?
2.30% приборов собирали рабочие первого участка автозавода. 70%
приборов - рабочие второго участка. Надежность приборов, собранных
рабочими первого участка, 0,9, второго - 0,8. Наудачу взятый прибор
оказался надежным. Найти вероятность того, что он изготовлен рабочими
первого участка.
3.В партии из 8 деталей имеется 6 стандартных. Наудачу отобраны 4 детали.
Составить закон распределения случайной величины
X - числа стандартных деталей среди отобранных. Найти математическое
ожидание и дисперсию случайной величины X.
4.Случайная величина X задана интегральной функцией распределения F(x):
F(x) =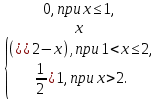
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4) вероятность попадания случайной величины X в интервал (1,5; 1,8);
5) построить графики F(x) и f(x).
ВАРИАНТ 4
1.На складе имеется 30 банок краски: 13 белой и 17 коричневой. Берутся
подряд две банки. Найти вероятность того, что: а) первая банка коричневая,
вторая белая; б) обе банки белые.
2.Каждое изделие проверяется одним из 2-х контролеров. Первый
LAB
отрезок прямой АВ: А(1;1), В(3;4).
ВАРИАНТ 4
1.Вычислить двойной интеграл ∫∫ x2ydxdyпо области D, ограниченной
D
линиями:у = 2 − х, у = х, х ≥ 0.
2. Вычислить площадь фигуры, ограниченной линиями: x = −2y2, x = 1−3y2, x ≤ 0, y≥ 0.
3. Вычислить тройной интеграл ∫∫∫(x2 + y2 + z2)dxdydz, если область V задается
V
неравенствами:0 ≤ х ≤ 3, −1 ≤ у ≤ 2, 0 ≤ z≤2.
4.Вычислить криволинейный интеграл ∫xydx + (y −x)dy + xydy, где LАB- дуга
LAB
кубической параболыу = х3 отточки А(0;0) до точки В(1;1).
ВАРИАНТ 5
1. Вычислить двойной интеграл ∫∫ (x3 −2y)dxdyпо области D, ограниченной
D
линиями:у = x2 −1, x≥ 0, y≤ 0.
2. Вычислить площадь фигуры, ограниченной линиями:у = х2 +1, x +y= 3.
3. Вычислить тройной интеграл∫∫∫x2y2zdxdydz, если область V задается
V
неравенствами: −1 ≤ x≤ 3, 0 ≤ у ≤ 2, − 2 ≤ z≤ 5.
4. Вычислить криволинейный интеграл ∫(x2+ y2)dx+(x +
y2)dy , где
LABC
LABC - ломаная ABC: А(1;2), В(3;2), С(3;5),
ВАРИАНТ 6
1. Вычислить двойной интеграл ∫∫ (y−x)dxdyпо области D, ограниченной
D
линиями:у = х2, х = у.
2. Вычислить площадь фигуры, ограниченной линиями: у2 = 4х, х2 = 4у.
3. Вычислить тройной интеграл ∫∫∫(x + y + z)dxdydz, если область V задается
V
задается неравенствами: 0 ≤ х ≤ 1, −l ≤ y≤ 0, l ≤ z≤ 2.
4. Вычислить криволинейный интеграл ∫xydx + (y −x)dy , где LOA- дуга
LOA
параболы у2 = xот точки O(0;0) до точки А(1;1).
ВАРИАНТ 7
1.Вычислить двойной интеграл ∫∫ (1+y)dxdyпо области D, ограниченной
D
линиями: у2 = х, 5у = х.
2.Вычислить площадь фигуры, ограниченной линиями: у = х2 + 2, х ≥ 0, х = 2, у = х.
3.Вычислить тройной интеграл ∫∫∫(2x − y2 −z)dxdydz, если область V задается
V
задается неравенствами: l ≤ x ≤ 5, 0 ≤ y ≤ 2, −l ≤ z ≤ 0.
4.Вычислить криволинейный интеграл ∫(xy-1)dx+ x2ydy , где LАB- дуга
LAB
параболы у2 = 4 − 4х от точки А(1;0) до точки В(0;2).
ВАРИАНТ 8
1.Вычислить двойной интеграл ∫∫ (x+y)dxdyпо области D, ограниченной
D
линиями: у = х2-1, у = −х2 +1.
2.Вычислить площадь фигуры, ограниченной линиями: у = х2, у = −х
.
3.Вычислить тройной интеграл ∫∫∫2xy2zdxdydz, если область V задается
V
неравенствами: 0 ≤ х ≤ 3, −2 ≤ у ≤ 0, 1 ≤ z ≤ 2.
4.Вычислить криволинейный интеграл ∫xydx + (y −x)dy , где LOA- дуга
LOA
параболы у= x2от точки O(0;0) до точки А(1;1).
ВАРИАНТ 9
1.Вычислить двойной интеграл ∫∫ x (y+1)dxdyпо области D, ограниченной
D
линиями: у = 5х, х = у, х = 3.
2.Вычислить площадь фигуры, ограниченной линиями: x= у2, x=
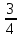y2+1. 3.Вычислить тройной интеграл ∫∫∫5xyz2dxdydz, если область V задается
V
неравенствами: −1≤ х ≤ 0, 2 ≤ у ≤ 3 1≤ z ≤ 2.
4.Вычислить криволинейный интеграл ∫(xy−y2)dx+ xdy , где LOA- дуга
LOA
параболы у = х2 от точки O(0;0) до точки А(1 ;1).
ВАРИАНТ 10
1.Вычислить двойной интеграл ∫∫ (x+2)ydxdyпо области D, ограниченной
D
линиями: у = х, у =
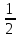х, х = 2.2.Вычислить площадь фигуры, ограниченной линиями: у = х2 +4х, у = х + 4.
3.Вычислить тройной интеграл ∫∫∫(x2+2y2 − z)dxdydz, если область V задается
V
неравенствами: 0 ≤ x≤ 1, 0 ≤ y≤ 3, −l ≤ z≤ 2.
4.Вычислить криволинейный интеграл ∫(xy − x
)dx+
x2dy , где LOA- дугаLOA
параболы у2 = 4х от точки O(0;0) до точки А(1;2).
КОНТРОЛЬНАЯ РАБОТА № 6
ВАРИАНТ 1
1.На пяти карточках написаны цифры от 1 до 5. Опыт состоит в случайном выборе трех карточек и раскладывании их в порядке поступления в ряд слева направо. Найти вероятности следующих событий: а) появится число 123; б) появится число, не содержащее цифры 3.
2.На фабрике, изготовляющей болты, первая машина производит 25% всех изделий, вторая 35% и третья - 40%. Брак в их продукции составляет соответственно 5%, 4% и 2%. Найти вероятность того, что случайно выбранный болт окажется бракованным.
3.В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения случайной величины X - числа стандартных деталей среди отобранных. Найти математическое ожидание и дисперсию случайной величины X.
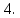Случайная величина X задана интегральной функцией распределения F(x):F(x) =
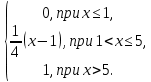
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4) вероятность попадания случайной величины X в интервал (2;3);
5) построить графики F(x) и f(x).
ВАРИАНТ 2
1.В ящике лежит 12 красных, 8 зелёных 10 синих шаров. Наудачу
вынимаются два шара. Найти вероятность того, что они разного цвета.
2.Два завода поставляют асфальтобетон одному ДСУ. Производительность
первого в два раза больше производительности второго завода. Первый завод
производит в среднем 60% асфальтобетона отличного качества, второй - 84%.
Наудачу взятая проба асфальтобетона, оказалась отличного качества. Найти
вероятность того, что этот бетон изготовлен на первом заводе.
3.В партии из 25 деталей имеется 6 бракованных. Наудачу отобраны три
детали. Составить закон распределения случайной величины
X - числа бракованных деталей среди отобранных. Найти математическое
ожидание и дисперсию случайной величины X.
4.Случайная величина X задана интегральной функцией распределения F(x):
F(x) =
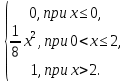
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4)вероятность попадания случайной величины X в интервал (0;1);\
5) построить графики F(x) и f(x).
ВАРИАНТ 3
1.На строительстве моста среди прочих машин используется 15
автогрейдеров и 10 бульдозеров. Необходимо выделить 5 машин на другой
объект. Какова вероятность того, что в их число попадут три автогрейдера и
два бульдозера?
2.30% приборов собирали рабочие первого участка автозавода. 70%
приборов - рабочие второго участка. Надежность приборов, собранных
рабочими первого участка, 0,9, второго - 0,8. Наудачу взятый прибор
оказался надежным. Найти вероятность того, что он изготовлен рабочими
первого участка.
3.В партии из 8 деталей имеется 6 стандартных. Наудачу отобраны 4 детали.
Составить закон распределения случайной величины
X - числа стандартных деталей среди отобранных. Найти математическое
ожидание и дисперсию случайной величины X.
4.Случайная величина X задана интегральной функцией распределения F(x):
F(x) =
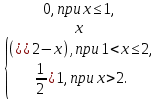
Найти: 1) Дифференциальную функцию f(x);
2) математическое ожидание случайной величины X;
3) дисперсию случайной величины X;
4) вероятность попадания случайной величины X в интервал (1,5; 1,8);
5) построить графики F(x) и f(x).
ВАРИАНТ 4
1.На складе имеется 30 банок краски: 13 белой и 17 коричневой. Берутся
подряд две банки. Найти вероятность того, что: а) первая банка коричневая,
вторая белая; б) обе банки белые.
2.Каждое изделие проверяется одним из 2-х контролеров. Первый