Файл: Условие равновесия в термодинамической системе Содержание.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
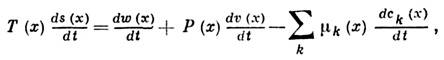
где
Статистическая физика позволяет уточнить понятие Л.Т.Р. и указать пределы его применимости. Понятию Л.Т.Р. соответствует локально равновесная функция распределения f плотности энергии, импульса и массы, которая отвечает максимуму информационной энтропии при заданных средних значениях этих величин как функций координат и времени:
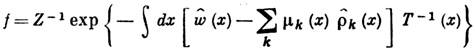
где Z - статистическая сумма,
2. Критерии обратимости в качестве критериев равновесия
Пользуясь тем, что п изохорно-изотермическом обратимом процессе dutU = Tdut S. Выведем критерии равновесия произвольной термодинамической системы, основываясь, на том, что равновесие – необходимое условие обратимости процесса и что, таким образом, каждое из состояний, через которые проходит система в обратимом процессе, оказывается состоянием равновесия. Отсюда следует: Критерии обратимости всегда являются вместе с тем критериями равновесия. Этим обстоятельством и пользуются в термодинамике: определяют состояния, в которых может происходить обратимый процесс, н каждое такое состояние считают состоянием равновесия. В настоящее время в термодинамике нет других средств нахождения состояний равновесия. Однако, пользуясь критериями обратимости вместо критериев равновесия, нужно помнить, что равновесие- необходимое, но недостаточное условие обратимости, т. с, что, кроме равновесных состояний, в которых может начаться обратимый процесс, существуют и такие равновесные состояния, в которых обратимый процесс невозможен. Из этого явствует, что, применяя критерии обратимости в качестве критериев равновесия, можно определить не все состояния равновесия, а только часть их. Этим объясняется тот хорошо известный факт, что все предсказанные термодинамикой состояния равновесия, действительно имеют место; но, кроме них, наблюдаются и такие состояния, которые термодинамикой не предсказываются. Между тем в некоторых таких смесях в довольно значительном интервале температур при постоянном объеме равновесный состав также остается постоянным, т. е. имеется непрерывный ряд равновесий и только одно из них указывается термодинамикой .
3. Некоторые условия устойчивости равновесия
Специальный термодинамический анализ позволяет показать, что из соображений термодинамической устойчивости системы для любого вещества должны выполняться следующие соотношения:
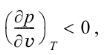 (2)
(2)т.е., во-первых, изохорная теплоемкость Сv всегда положительна и, во-вторых, в изотермическом процессе увеличение давления всегда приводит к уменьшению объема вещества. Условие (1) называют условием термической устойчивости
, а условие (2) – условием механической устойчивости. Условия (1) и (2) можно объяснить так называемым принципом смещения равновесия (принцип Ле Шателье – Брауна), смысл которого заключается в том, что, если система, находившаяся в равновесии, выводится из него, соответствующие параметры системы изменяются таким образом, чтобы система вернулась в состояние равновесия. Эти условия термодинамической устойчивости системы ясны и без формальных выкладок. Представим себе, что теплоемкость сv некоторого вещества отрицательна. Это означало бы, поскольку cv = dqv/dT, что подвод теплоты к веществу при постоянном объеме этого вещества приводил бы не к повышению, а к понижению температуры. Таким образом, чем больше теплоты мы подводили бы к веществу в изохорном процессе, тем больше становилась бы разность между температурами этого вещества и источника теплоты (окружающая среда).
Для вывода условий устойчивости можно предположить, что при малом отклонении от положения равновесия система однородна по внутренним параметрам T иp, ноTTo,PPo, пока не достигнуто равновесие. Можно обойтись и без этого предположения и рассмотреть не всю систему, а столь малую ее часть, что ее можно считать однородной поTиp. Результат будет получен один и тот же. Согласно (49) запишем
dU-TcdS+pcdV=-Tc(diS+diSпов)
Если система выведена из условия устойчивого равновесия, то поскольку правая часть положительна, то
dU-TcdS+pcdV>0.
При малом, но не бесконечно малом отклонении от устойчивого равновесия должно быть
U-TcS+pcV>0 (51)
При этом U=TS-pV . Подставляя это выражение в (51) получим условия устойчивости равновесия в виде
TS-pV>0, (52)
где T=T-Tc,p=p-pc отклоненияT иp от равновесных значений поскольку в равновесииT=Tc, p=pc.
Для изобарных (p=0) и изохорных (V=0) систем условия устойчивости равновесия (52) принимают видTS>0
Будем неограниченно приближать систему к равновесию, меняя S. Тогда
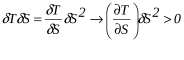
В изобарных и изохорных условиях
Следовательно, условие устойчивости изобарного равновесия имеет вид
, (53)то есть
Условие устойчивости изохорного равновесия
В изотермической (T=0)и изэнтропической (S=0)системах условие (52) принимает видpV<0. Будем неограниченно приближать систему к равновесию, меняя V. Тогда
в изотермических, а в изэнтропических условиях
Следовательно, условие устойчивости изотермического равновесия имеет вид
Для изэнтропического равновесия -
Неравенства , ,
Термодинамическое равновесие неустойчиво, если сколь угодно малые флуктуации выводят систему в такое неравновесное состояние, из которого она не возвращается в исходное равновесное, а движется к некоторому иному равновесному.
Следует отметить, что, если в данных условиях рассматриваемое равновесное состояние оказывается неустойчивым (не выполнены условия устойчивости), то при этих условиях существует непременно некоторое иное, устойчиво равновесное состояние. Система не может находиться в неустойчивом равновесии сколь - нибудь долго. Понятие неустойчиво равновесное состояния достаточно условно. Строго говоря, неустойчиво равновесные состояния не реализуются. Могут существовать лишь неравновесные состояния, в какой-то мере близкие или приближающиеся к неустойчиво равновесным.
Если выполнены все условия устойчивости (54),(56),(57),(58), то все четыре характеристик CP,CV,ST положительны. При этом ,как видно, из (43)CP>CVи, как следует из (37)T>S.
Как видно из (36), Pможет быть и положительным и отрицательным; знакPне определяется условиями устойчивости, Из опыта известно, что почти всегдаP>0. При этом, как следует из (39) и (40) изохорный и адиабатический коэффициенты давления
Список использованных источников
1Сорокин, В. С. Макроскопическая необратимость и энтропия. Введение в термодинамику. / В.С. Сорокин. – М.: ФИЗМАТЛИТ, 2004. – 176 с.
2Михеева, Е.В. Физическая и коллоидная химия: учебное пособие / Е.В.Михеева, Н.П.Пикула; Томский политехнический университет. – Томск: ТПУ, 2010. – 267 с.
3Де Гроот, С. Неравновесная термодинамика. / С. Де Гроот, П. Мазур. М.: Мир, 1964. – 456 с.
4Химия и химическая технология / Некоторые условия устойчивости равновесия [Электронный ресурс] // URL: http://www.chem21.info/page/104.html (дата обращения 18.04.2016).

