ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.02.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 1
Тема 1.1. Основные понятия алгебры высказываний
Задание 1
Составив таблицы истинности, выясните, равносильны ли формулы алгебры высказываний из таблицы 1.1.
Таблица 1.1
| № вари-анта | Формулы |
| 1 | 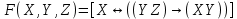 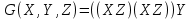 |
| 2 | 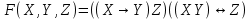 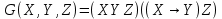 |
| 3 | 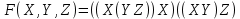 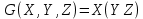 |
| 4 | 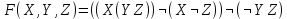 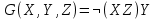 |
| 5 | 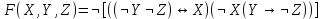 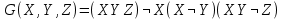 |
| 6 | 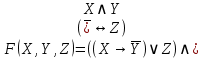 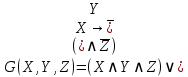 |
| 7 | 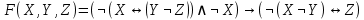 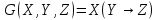 |
| 8 | 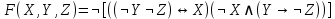 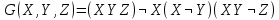 |
| 9 | 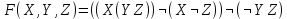 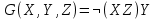 |
| 10 | 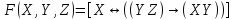 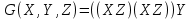 |
Рекомендации по выполнению задания
Номер варианта задания определить по первой букве фамилии студента, используя таблицу 1.2. Решение расписывать как можно подробнее,
обязательно описывать формулы, используемые при решении. Обязательно должны быть записаны условие задания, ответ.
Таблица 1.2
Выбор варианта задания
| Буква | А, Ф, Э | Б, М, Х | В, Ю | Г, У,Я | Д, Ч, С | Е, Н, П | Ж, О, З | И, Ц | К, Т, Ш, Щ | Л, Р |
| № вар. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Образец выполнения задания
Задание
Составив таблицы истинности, выясните, равносильны ли следующие формулы алгебры высказываний:
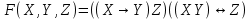 ,
,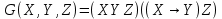 .
.Решение
Будем использовать таблицы истинности конъюнкции, дизъюнкции, импликации и эквивалентности.
| X | Y |  |  | 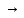 | 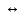 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Таблица истинности формулы F
| X | Y | Z | 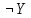 | 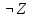 | 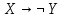 | 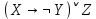 | 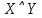 | 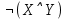 | 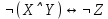 | 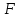 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
Таблица истинности формулы G
| X | Y | Z | 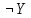 | 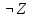 | 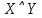 | 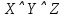 | 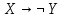 | 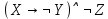 | 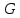 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
Формулы F и G не эквивалентны, так как их значения различаются на наборе (1, 1, 1).
Введённая функция:
X∧(Y→Z)∨¬X∨¬Z≡¬¬Y≡Z
Вектор функция: 00111011
Таблица истинности:
| X | Y | Z | Y→Z | X∧(Y→Z) | ¬Z | X∨¬Z | ¬X∨¬Z | X∧(Y→Z)∨¬X∨¬Z | ¬Y | ¬Y≡Z | ¬¬Y≡Z | X∧(Y→Z)∨¬X∨¬Z≡¬¬Y≡Z |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
Совершенная дизъюнктивная нормальная форма (СДНФ)
¬XY¬Z ∨ ¬XYZ ∨ X¬Y¬Z ∨ XY¬Z ∨ XYZ
Совершенная конъюнктивная нормальная форма (СKНФ)
(X∨Y∨Z) ∧ (X∨Y∨¬Z) ∧ (¬X∨Y∨¬Z)
Полином Жегалкина
Y⊕X⊕XZ⊕XY⊕XYZ
Решение
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 0 } { 1, 1, 0 } { 1, 1, 1 }
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
K1: { 0, 1, 0 } — ¬XY¬Z
K2: { 0, 1, 1 } — ¬XYZ
K3: { 1, 0, 0 } — X¬Y¬Z
K4: { 1, 1, 0 } — XY¬Z
K5: { 1, 1, 1 } — XYZ
Объединим конъюнкции с помощью операции ИЛИ и получим совершенную дизъюнктивную нормальную форму:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬XY¬Z ∨ ¬XYZ ∨ X¬Y¬Z ∨ XY¬Z ∨ XYZ
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 0, 0, 1 } { 1, 0, 1 }
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
D1: { 0, 0, 0 } — X∨Y∨Z
D2: { 0, 0, 1 } — X∨Y∨¬Z
D3: { 1, 0, 1 } — ¬X∨Y∨¬Z
Объединим дизъюнкции с помощью операции И и получим совершенную конъюнктивную нормальную форму:
D1 ∧ D2 ∧ D3 = (X∨Y∨Z) ∧ (X∨Y∨¬Z) ∧ (¬X∨Y∨¬Z)
Построение полинома Жегалкина методом Паскаля:
| X | Y | Z | ((X∧(Y→Z))∨¬(X∨¬Z))≡¬(¬Y≡Z) | | | | | | | |
| 0 | 0 | 0 | 0 | → | 0 | → | 0 | → | 0 | |
| 0 | 0 | 1 | 0 | ⊕ 0 | 0 | → | 0 | → | 0 | |
| 0 | 1 | 0 | 1 | → | 1 | ⊕ 0 | 1 | → | 1 | Y |
| 0 | 1 | 1 | 1 | ⊕ 1 | 0 | ⊕ 0 | 0 | → | 0 | |
| 1 | 0 | 0 | 1 | → | 1 | → | 1 | ⊕ 0 | 1 | X |
| 1 | 0 | 1 | 0 | ⊕ 1 | 1 | → | 1 | ⊕ 0 | 1 | XZ |
| 1 | 1 | 0 | 1 | → | 1 | ⊕ 1 | 0 | ⊕ 1 | 1 | XY |
| 1 | 1 | 1 | 1 | ⊕ 1 | 0 | ⊕ 1 | 1 | ⊕ 0 | 1 | XYZ |


