Файл: Обыкновенные дроби при реализации системнодеятельностного подхода 13.docx

Мотивационно-ценностный этап характеризуется созданием ситуации в которой происходит положительное самоопределение ученика деятельности на уроке. Речь идет о создании таких условий, в которых возникает внутренняя потребность включения в деятельность. Отметим, что для ученика основной школы, в том числе и 5-6 класса главным видом деятельности является обучение в школе. Существенная особенность такой деятельности учеников 5-6 класса заключается избирательной готовности к тем или иным сторонам обучения. В этом плане высока роль мотивов. Ребенок такого возраста проявляет большую готовность к тем видам учебной деятельности, в которых он выглядит взрослым в собственных глазах. Наибольший интерес вызывают самостоятельные формы организации занятий на уроке, сложный учебный материал, возможность самому строить свою познавательную деятельность вне урока. Однако ребенок 5-6 класса не всегда осуществлять такую деятельность. Основная неудача учащихся в учебно-познавательной деятельности в таком возрасте связана несформированности у учащихся способов учебной деятельности, что не дает возможности реализовать актуальную потребность ученика данного возраста – потребность в самоутверждении. Естественно для повышения эффективности обучения учеников является целенаправленное формирование у них мотивов учения [1].

Процессуальный этап предполагает организацию деятельности учащихся по «открытию» нового знания и его применению.

Рефлексивно-оценочный этап связан с фиксированием освоенного содержания, изученного на уроке, с последующей рефлексией, самооценкой и взаимооценкой учениками деятельности на уроке. Устанавливается степень соответствия поставленной цели на первом этапе и результатов осуществленной деятельности, определяются цели последующей деятельности.

Отметим, что основу деятельности учеников 5-6 классов составляют мотивы. Это связано с психологическими особенностями данного возраста. Для этого возрастного периода важно наличие познавательного интереса, познавательной потребности. Кроме того, необходимо чтобы ученики осознавали для чего им нужны знания, освоенные на уроке, а также их содержание, оно должно быть интересным и жизненным. Только в таком случае обучение будет осознанным. Кроме того велика роль самооценки учащихся своих способностей и знаний [5].

Как видно из вышеизложенного, психические процессы характерные для учеников 5-6 классов, существенно влияют на процесс усвоения знаний и умений. Поэтому их учёт их необходим для организации успешного обучения учащихся. Соответственно данные факты нашли отражение и в организационной структуре урока в формате СДП.

---

Уроки деятельностной направленности по целеполаганию можно распределить на три группы:

1. уроки «открытия» нового знания;

2. уроки рефлексии;

3. уроки развивающего контроля [5].

Этапы каждого из видов урока повторяют этапы деятельности, выделенные нами в предыдущем параграфе. Поэтому структура любого урока в формате СДП содержит такие структурные этапы:

1. Мотивация (самоопределение) к учебной деятельности.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии.

3. Постановка проблемы.

4. Построение проекта выхода из затруднения.

5. Реализация построенного проекта.

6. Первичное закрепление с проговариванием во внешней речи.

7. Самостоятельная работа с самопроверкой по эталону.

8. Включение в систему знаний и повторение.

9. Рефлексия учебной деятельности [6].

В нашем исследовании мы придерживаемся мнения, что для успешной реализации урока основанного на системно деятельностном подходе, необходимо провести тщательную его подготовку. В связи с этим логично обратиться к методическим вопросам проектирования таких уроков [8].

Поэтому в процессе подготовки урока в формате СДП мы предлагаем разрабатывать и использовать технологическую карту урока, которая содержит:

 название темы;

 планируемые результаты (личностные, метапредметные, предметные);

 тип урока (учебного занятия), определяющий технологию [6]

Учителю следует обратить внимание на следующие: разбиение учебного процесса на уроки разных типов в соответствии с ведущими целями не должно разрушать его непрерывность, а значит, необходимо обеспечить инвариантность технологии обучения. Поэтому при построении технологии организации уроков разных типов должен деятельностный метод обучения и обеспечиваться соответствующая ему система дидактических принципов как основа для построения структуры и условий взаимодействия между учителем и учеником.

Раздел 2. Методические аспекты реализации системно-деятельностного подхода при изучении темы обыкновенные дроби

2.1. Комплекс задач по теме «Обыкновенные дроби» при реализации системно-деятельностного подхода

1. Среди данных математических предложений выбрать те, которые сформулированы правильно.

Пример. Выберите правильную формулировку определения:

− неправильной называется дробь, у которой числитель больше знаменателя; (Л)

− правильной называется дробь, у которой числитель больше знаменателя; (Л)

---

− неправильной называется дробь, у которой числитель не меньше знаменателя; (И)

− правильной называется дробь, у которой числитель не больше знаменателя; (Л)

− неправильной называется дробь, у которой числитель равен знаменателю; (И)

− правильной называется дробь, у которой числитель меньше знаменателя; (И)

2. Решить задачу с недостающими (лишними, противоречивыми) данными, с необычной фабулой или постановкой вопроса.

Пример. Какие данные противоречивы?

− Дана правильная дробь, числитель которой кратен 3 а знаменатель равен 2. Найдите все такие дроби.

Пример. Измените условие задачи так, чтобы она имела единственное решение:

− В соревновании участвовало 140 спортсменов. В каждой команде было по 8 мужчин. Сколько всего было женщин, если в команде их было меньше, чем мужчин?

3. В 56-х классах, когда учащиеся еще только осваивают предложенную деятельность, учитель может быть инициатором первых (разных) версий решения проблемы.

Пример. Сравните несколько предложенных дробей.



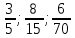
Удобно ли сравнивать эти дроби, применяя данный порядок действий? Чем он удобен? Предложите другой способ сравнения этих дробей, какие средства вам «подскажут» способ – справочник по математике, интернет-ресурсы или другие источники? Какие еще способы сравнения дробей вы обнаружили в используемом источнике? Приведите пример пары таких дробей, которые удобнее сравнивать, используя другой порядок действий.

4. Сформулировать задачу, аналогичную (обратную, частично измененную) данной типовой задаче.

Пример. Дана задача: в классе 24 ученика писали контрольную работу по математике. Сколько учеников справилось с работой на «отлично», если они составили 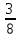от всего количества учащихся?

− прочитайте эту задачу;

− если в дайной задаче будет известно количество детей, не справившихся с контрольной работой, то можно ли ответить на вопрос задачи?

− придумайте задачу, которая решается по такому же алгоритму;

− придумайте задачу, обратную данной;

− как можно решить обратную задачу, используя приѐм решения данной?

---

5. Пример. Выполните деление столбиком десятичной дроби (придумайте сами) на 10, 100, 1000,. Составьте таблицу

Данн ое число	Результат деления на
	10	100	1000	10000

Проанализируйте получившиеся результаты, сформулируйте гипотезу о получившейся закономерности.

Пример. Выполните умножение десятичных дробей. Заполните таблицу, которая представлена выше. Сформулируйте правило умножения десятичных дробей.

6. Подобрать для соседа по парте задания определенного вида решения на этапе повторения и предложить ему их решить, организовать работу над ошибками. Оценка качества выполненной работы одноклассника.

Пример. Составить 10 заданий на последовательное процентное изменение величины:

• 
  двойное повышение на одно и то же число процентов;
  
• 
  двойное понижение на одно и то же число процентов;
  
• 
  двойное повышение на разное число процентов;
  
• 
  двойное понижение на разное число процентов;
  
• 
  повышение, а затем понижение на одно и то же число процентов;
  
• 
  понижение, а затем повышение на одно и то же число процентов;
  
• 
  повышение, а затем понижение на разное число процентов;
  
• 
  понижение, а затем повышение на разное число процентов.
  

7. Измените условие задачи так, чтобы она имела единственное решение:

− Числа, являющиеся числителем и знаменателем дроби, отличаются на 1 одно из этих чисел равно 7. Найдите эту дробь.

Для сравнения дробей с разными знаменателями чаще всего применяется следующий порядок действий:

− найти наименьшее общее кратное для чисел, стоящих в знаменателях дробей;

− найти дополнительные множители для знаменателей;

− умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель; сравнить полученные числа.

2.2. Методы и приемы обучения, позволяющие реализовывать системно-деятельностный подход при изучении обыкновенных дробей

---

Классификация методов по характеру познавательной деятельности.

Объяснительно-иллюстративный метод, метод при котором преподаватель объясняет, а школьники воспринимают, осознают и фиксируют в памяти.

Репродуктивный метод (воспроизведение и применение информации)

Метод проблемного изложения (постановка проблемы и показ пути ее решения)

Частично – поисковый метод (студенты пытаются сами найти путь к решению проблемы)

Исследовательский метод (преподаватель направляет, студенты самостоятельно исследуют).

Наиболее продуктивным и интересным считаю создание проблемной ситуации, исследование, поиск правильного ответа.

Для развития познавательных интересов стараюсь выполнять следующие условия [9]:

1. 
   избегать в стиле преподавания будничности, монотонности, серости, бедности информации, отрыва от личного опыта студента;
   
2. 
   не допускать учебных перегрузок, переутомления и низкой плотности режима работы использовать содержание обучения как источник стимуляции познавательных интересов;
   
3. 
   стимулировать познавательные интересы многообразием приемов занимательности
   
4. 
   (иллюстрацией, игрой, кроссвордами, задачами-шутками, занимательными упражнениями т.д.);
   
5. 
   специально обучать приемам умственной деятельности и учебной работы, использовать проблемно-поисковые методы обучения.
   

Знания будут прочными, если они приобретены не одной памятью, не заучены механически, а являются продуктом собственных размышлений и проб и закрепились в результате его собственной творческой деятельности над учебным материалом.

Творческие, поисковые, проблемные задания позволяют создавать на уроках кратковременные педагогические ситуации для познавательной деятельности учащихся, обеспечивающих более полное включение их в самостоятельное выполнение.

На этапах «открытия» новых знаний важным становится организация самостоятельной деятельности учащихся, в процессе которой они выполняют проблемные и другие творческие задания (практические, лабораторные работы, проводят эксперимент). В результате этой деятельности получают «продукт» - вывод, определение понятия, формулировку математического предложения, выдвигают гипотезы, которые в дальнейшей работе проверяются, либо опровергаются. К проблемным заданиям можно отнести практическую и лабораторную работы, учебные исследования, основанные на эмпирических методах [14].

К творческим заданиям можно отнести занимательные задания и задачи, дидактические игры, творческие задания для самостоятельной работы при изучении нового материала, обобщения и систематизации. Выполняя творческие задания, ученик в большей степени становится субъектом учебной деятельности, вступает в диалог с учителем, активно участвует в познавательном процессе.

---