Файл: Курсовая работа электропроводность горных пород студента iv курса геологического факультета Логинова Александра Алексеевича.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 20
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ех, Ну :
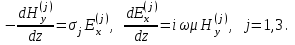
Во втором анизатропном слое электромагнитное поле определяется компонентами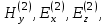
связанные соотношениями
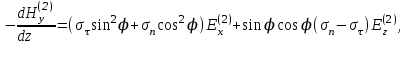
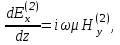
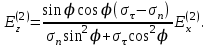
Последнее равенство в (4) есть следствие того, что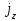
= 0, где 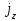– составляющая плотности тока проводимости. Таким образом, хотя 
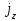≠ 0, но = 0. Такая связь напряженности электрического поля и тока проводимости возможна в анизатропной среде, но не допустима в изотропной. Уравнение (3), (4) дополняются на поверхности раздела 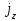= 0, z= h3 краевыми условиями
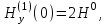
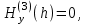
а на поверхностях z= h1,z= h2 условиями сопряжения
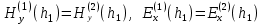
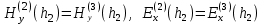
Подставляя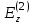
из последнего равенства (4) в первое уравнение той же группы формул и исключая компоненту 
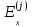, j = 1,2,3 из (3), (4), (7), (8), получим уравнение для компоненты 
:
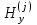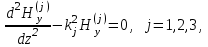
где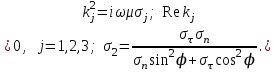
Решение задачи (5)-(9) хорошо известно [Бердичевский, Жданов, 1981] и по формуле Ваньяна-Липской для импеданса Z Тихонова-Каньяра можно записать:
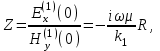
где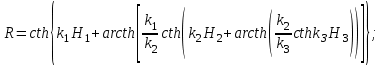
H1 = h1, H2 = h2-h1, H3 = h3-h2– мощности 1,2 и 3 слоев соответственно.
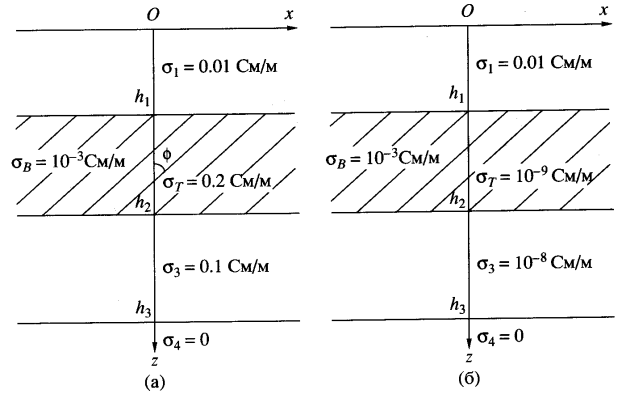
Рис. 3. Модели разуплотненных структур: трещиноватый 2-й слой заполнен минерализованной водой (а), нефтью или газом (б).
Для вариантов четырехслойной модели среды (рис. 3) были рассчитаны амплитудные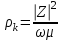
и фазовые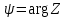
кривые магнитотеллурических зондирований (МТЗ). В обоих вариантах H1= 50м, H2 = 5000м, H3 = 5000м, 
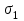= 10-2СМ/м, 
, 
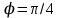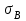= 10-3 СМ/м. Однако в первом случае третий слой низкоомный (
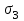= 10-1 СМ/м), а во втором случае высокоомный ( 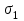= 10-8 СМ/м). Как в том, так и в другом случаях трещины во втором слое заполняются флюидом, поступающим из третьего слоя. В первом варианте 
= 0.2СМ/м, что соответствует минерализованной среде, а во втором случае – трещины заполняются высокоомным флюидом (например, газом или нефтью) и поэтому = 10-9 СМ/м.
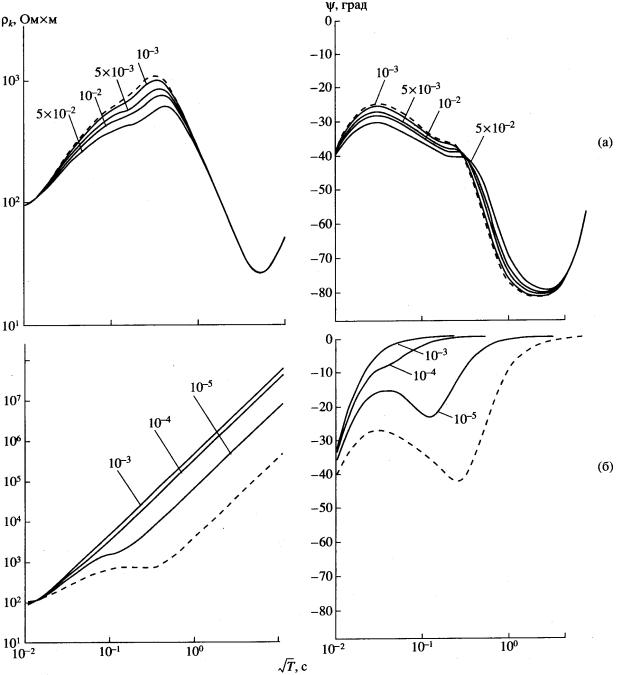
Рис. 4. Амплитудные и фазовые кривые МТЗ для трещиноватого слоя, заполненного минерализованной водой (а), нефтью или газом (б). Шифр кривых
.
В случае заполнения трещин минерализованной водой ( рис. 3а) кривые МТЗ представлены на рис. 4а для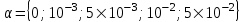
.
Значению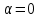
соответствует отсутствие трещин во втором слое. Здесь и в дальнейшем кривые электромагнитного поля для этого значения будем изображать пунктирной линией. Изменение амплитудных кривых становится более значимым с ростом доли трещин, а фазовые кривые МТЗ слабо зависят от изменения . На рис. 4б следует, что по результатам МТЗ могут быть обнаружены самые ранние моменты трещинообразования во втором слое. Именно прослеживание изменений электромагнитных полей с незначительными и, очевидно, медленными процессами трещинообразования, как следствия напряженно-деформируемых состояний горных пород, и является основной целью прогноза динамики разуплотнения. В отличии от первого варианта модели четырехслойной среды, с увеличением доли трещин различие кривых МТЗ становится все менее заметным, а процесс раннего трещинообра
зования хорошо определяется как по амплитудным, так и по фазовым кривым.
Аналогично поведение кривых электромагнитного поля в случае зондирований становлением поля. Пусть на поверхности четырехслойной среды (рис. 3) расположен вертикальный магнитный диполь, момент которого в отсчет времени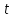
= 0 скачкообразно изменяется с некоторого постоянного значения до нуля. Для расчета кривых становления электромагнитного поля приближенно будем считать второй слой изотропным с эффективной электропроводностью 
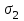, вычисляемой так же, как в рассмотренном случае МТЗ. Этот случай соответствует пористой среде или среде с неупорядоченным и статистически равномерным распределением трещин по области второго слоя. Тогда, напряженность электрического поля имеет единственную отличную от нуля азимутальную компоненту 
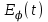. Для двух вариантов модели четырехслойной среды и для разноса 
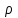= 1000м рассчитаны кривые
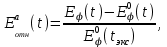
где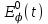
- азимутальная компонента напряженности электрического поля при = 0 (трещины или поры во втором слое отсутствуют)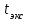 
время, на котором аномальное поле 
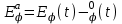достигает первого экстремального значения. На рис. 5 значения 
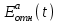отложены в линейном масштабе, а время t – в логарифмическом. Кривые 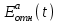для модели, изображенной на рис. 3а, представлены на рис. 5а для значений 
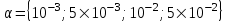. До момента времени t = 10-5с 
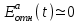, то есть до этого момента значения 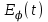практически не отличаются от значений 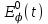. При дальнейшем увеличении времени кривые 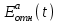переходят в момент времени t=tэкс через отрицательный минимум, а затем – через положительный максимум и в пределе стремятся к нулю при 
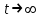. При увеличении возрастает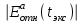 
. С уменьшением значения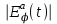 
стремятся к нулю. Кривые 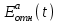для модели на рис. 3б и 
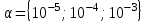изображены на рис. 5б. Также как в предыдущем случае 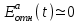до момента времени
t = 10-5с. Затем, с увеличением t кривые
достигают положительного максимума при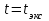 
, переходят через отрицательный минимум и стремятся к нулю. Из рис. 5б следует, что при заполнении трещин высокоомным флюидом максимальное значение тем больше, чем больше доля трещин, хотя при 
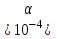кривые уже мало отличаются друг от друга. Знак экстремума кривых может служить признаком того, каким флюидом наполнены трещины: при заполнении трещин минерализованной средой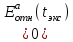 
, а при заполнении газом или нефтью 
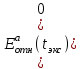. Таким образом, поведение кривых существенно отличается в зависимости от электропроводности флюида, наполняющего трещины, и доли трещин в среде.
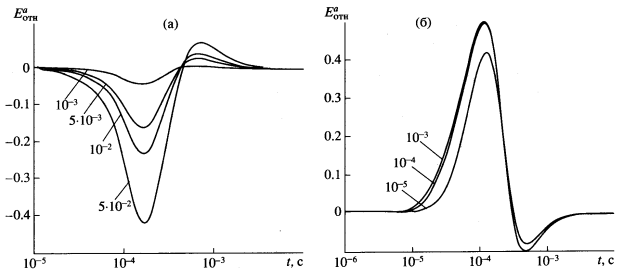
Рис. 5. Относительная азимутальная компонента становления поля вертикального магнитного диполя для разуплотненного слоя с минерализованной водой (а), нефтью или газом (б). Шифр кривых
ЗАКЛЮЧЕНИЯ
СПИСОК ЛИТЕРАТУРЫ
Размещено на .ur1>1>
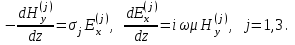
Во втором анизатропном слое электромагнитное поле определяется компонентами
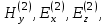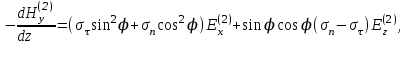
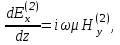
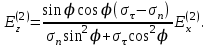
связанные соотношениями Последнее равенство в (4) есть следствие того, что
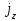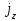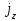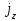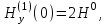
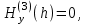
= 0, где – составляющая плотности тока проводимости. Таким образом, хотя ≠ 0, но = 0. Такая связь напряженности электрического поля и тока проводимости возможна в анизатропной среде, но не допустима в изотропной. Уравнение (3), (4) дополняются на поверхности раздела = 0, z= h3 краевыми условиями а на поверхностях z= h1,z= h2 условиями сопряжения
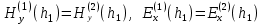
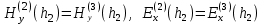
Подставляя
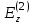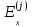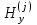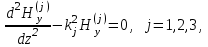
из последнего равенства (4) в первое уравнение той же группы формул и исключая компоненту , j = 1,2,3 из (3), (4), (7), (8), получим уравнение для компоненты : где
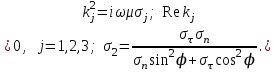
Решение задачи (5)-(9) хорошо известно [Бердичевский, Жданов, 1981] и по формуле Ваньяна-Липской для импеданса Z Тихонова-Каньяра можно записать:
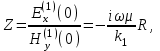
где
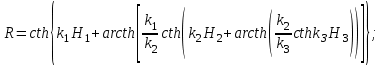
H1 = h1, H2 = h2-h1, H3 = h3-h2– мощности 1,2 и 3 слоев соответственно.
Рис. 3. Модели разуплотненных структур: трещиноватый 2-й слой заполнен минерализованной водой (а), нефтью или газом (б).
Для вариантов четырехслойной модели среды (рис. 3) были рассчитаны амплитудные
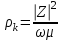
и фазовые
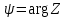кривые магнитотеллурических зондирований (МТЗ). В обоих вариантах H1= 50м, H2 = 5000м, H3 = 5000м, 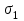= 10-2СМ/м, 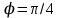, 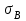= 10-3 СМ/м. Однако в первом случае третий слой низкоомный ( 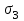= 10-1 СМ/м), а во втором случае высокоомный ( 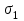= 10-8 СМ/м). Как в том, так и в другом случаях трещины во втором слое заполняются флюидом, поступающим из третьего слоя. В первом варианте = 0.2СМ/м, что соответствует минерализованной среде, а во втором случае – трещины заполняются высокоомным флюидом (например, газом или нефтью) и поэтому = 10-9 СМ/м. Рис. 4. Амплитудные и фазовые кривые МТЗ для трещиноватого слоя, заполненного минерализованной водой (а), нефтью или газом (б). Шифр кривых
.В случае заполнения трещин минерализованной водой ( рис. 3а) кривые МТЗ представлены на рис. 4а для
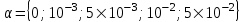. Значению
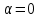соответствует отсутствие трещин во втором слое. Здесь и в дальнейшем кривые электромагнитного поля для этого значения будем изображать пунктирной линией. Изменение амплитудных кривых становится более значимым с ростом доли трещин, а фазовые кривые МТЗ слабо зависят от изменения . На рис. 4б следует, что по результатам МТЗ могут быть обнаружены самые ранние моменты трещинообразования во втором слое. Именно прослеживание изменений электромагнитных полей с незначительными и, очевидно, медленными процессами трещинообразования, как следствия напряженно-деформируемых состояний горных пород, и является основной целью прогноза динамики разуплотнения. В отличии от первого варианта модели четырехслойной среды, с увеличением доли трещин различие кривых МТЗ становится все менее заметным, а процесс раннего трещинообра
зования хорошо определяется как по амплитудным, так и по фазовым кривым.
Аналогично поведение кривых электромагнитного поля в случае зондирований становлением поля. Пусть на поверхности четырехслойной среды (рис. 3) расположен вертикальный магнитный диполь, момент которого в отсчет времени
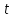= 0 скачкообразно изменяется с некоторого постоянного значения до нуля. Для расчета кривых становления электромагнитного поля приближенно будем считать второй слой изотропным с эффективной электропроводностью 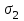, вычисляемой так же, как в рассмотренном случае МТЗ. Этот случай соответствует пористой среде или среде с неупорядоченным и статистически равномерным распределением трещин по области второго слоя. Тогда, напряженность электрического поля имеет единственную отличную от нуля азимутальную компоненту 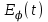. Для двух вариантов модели четырехслойной среды и для разноса 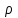= 1000м рассчитаны кривые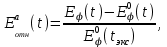 где
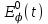- азимутальная компонента напряженности электрического поля при = 0 (трещины или поры во втором слое отсутствуют) 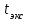время, на котором аномальное поле 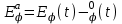достигает первого экстремального значения. На рис. 5 значения 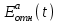отложены в линейном масштабе, а время t – в логарифмическом. Кривые 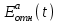для модели, изображенной на рис. 3а, представлены на рис. 5а для значений 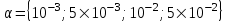. До момента времени t = 10-5с 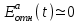, то есть до этого момента значения 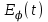практически не отличаются от значений 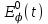. При дальнейшем увеличении времени кривые 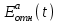переходят в момент времени t=tэкс через отрицательный минимум, а затем – через положительный максимум и в пределе стремятся к нулю при 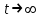. При увеличении возрастает 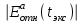. С уменьшением значения 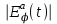стремятся к нулю. Кривые 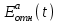для модели на рис. 3б и 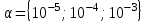изображены на рис. 5б. Также как в предыдущем случае 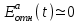до момента времени
t = 10-5с. Затем, с увеличением t кривые
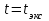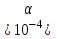достигают положительного максимума при , переходят через отрицательный минимум и стремятся к нулю. Из рис. 5б следует, что при заполнении трещин высокоомным флюидом максимальное значение тем больше, чем больше доля трещин, хотя при кривые уже мало отличаются друг от друга. Знак экстремума кривых может служить признаком того, каким флюидом наполнены трещины: при заполнении трещин минерализованной средой 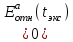, а при заполнении газом или нефтью 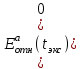. Таким образом, поведение кривых существенно отличается в зависимости от электропроводности флюида, наполняющего трещины, и доли трещин в среде. Рис. 5. Относительная азимутальная компонента
становления поля вертикального магнитного диполя для разуплотненного слоя с минерализованной водой (а), нефтью или газом (б). Шифр кривых ЗАКЛЮЧЕНИЯ
-
Эффективная электропроводность горных пород может заметно изменяться при возникновении в них относительно малой доли трещин. -
При заполнении трещин высокоомным флюидом прогноз раннего трещинообразования методами электроразведки возможен для напряженности электрического поля, ориентированной поперек направления трещин, а при заполнении низкоомным флюидом – вдоль. -
Если трещины наполняются высокоомным флюидом, то изменение электромагнитного поля может быть замечено на ранних этапах трещинообразования, при 0,001% доле трещин. С увеличением доли трещин изменения электромагнитного поля становится менее значимым. В случае же заполнения трещин низкоомным флюидом (например, минерализованной водой) изменение электромагнитного поля наиболее заметно при более 0,1% трещин во вмещающей среде. -
По знаку аномального сигнала становления поля можно судить о проводимости флюида, наполняющего трещины.
СПИСОК ЛИТЕРАТУРЫ
-
Бердичевский М.Н., Жданов М.С. Интерпретация аномалий переменного электромагнитного поля Земли. М.: Недра, 1981. 327 с. -
Бурсиан В.Р. Теория электромагнитных полей, применяемых в электроразведке. Л.: Недра, 1972. 368 с. -
Губатенко В.П. Эффект Максвелла-Вагнера в электроразведке//Изв. АН СССР. Физика Земли. 1991. №4. С. 88-98. -
Губатенко В.П., Бердичевский М.Н., Светов Б.С. Магнитотеллурическое зондирование вертикально-трещиноватых сред //Изв. АН СССР. Физика Земли. 1992. №4. С. 3-17. -
Николаевский В.Н. Геомеханика и флюидодинамика. М.: Недра, 1996. 447 с. -
Огаджанов В.А. Концепция геофизических исследований, основанная на явлении дилатации горных пород // Геофизика. 1998. №4. С. 10-14. -
Уэйт Дж. Р. Геоэлектромагнетизм: Пер. с англ. Ред. пер. Бердичевский М.Н. М.: Недра, 1987. 235 с.
Размещено на .ur1>1>