Файл: Признаки и свойства параллельности прямых и плоскостей Признак параллельности прямых в пространстве.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Признаки и свойства параллельности прямых и плоскостей | |
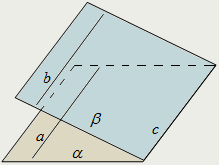 | Признак параллельности прямых в пространстве: Две прямые, параллельные третьей прямой, параллельны между собой: a||c, b||c ⇒ a||b. |
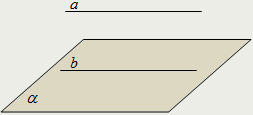 | Признак параллельности прямой и плоскости: Прямая, не лежащая в плоскости, параллельна этой плоскости тогда и только тогда, когда она параллельна некоторой прямой в этой плоскости: а ∉ α, ∃b ∈ α, а || b ⇔ а || α. |
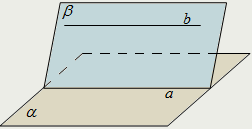 | Признак параллельности прямых в пространстве: Если прямая, лежащая в одной из пересекающихся плоскостей, параллельна другой плоскости, то она параллельна их линии пересечения. b || α, α ∩ β = a ⇒ а || b. |
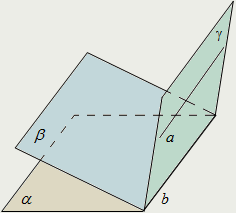 | Признак параллельности прямых в пространстве: Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии пересечения этих плоскостей: a || α, a || β, α ∩ β = b ⇒ а || b. |
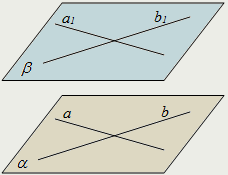 | Признак параллельности плоскостей: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны: a ∈α, b ∈ α, a1∈ β, b1∈β, a ∩ b ⇓ α || β. |
| Некоторые свойства прямых и плоскостей | |
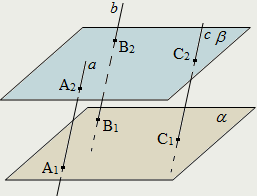 | Отрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны: α||βи a || b || c ⇒ A1A2 = B1B2 = C1C2 . |
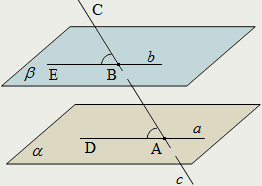 | Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость; более того, эта прямая образует с параллельными плоскостями равные углы: α || β ⇒ ∠CBE = ∠CAD. |
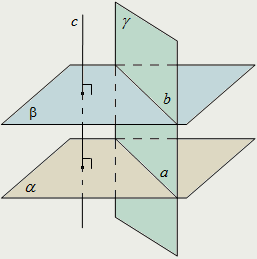 | Прямые, полученные при пересечении двух параллельных плоскостей третьей плоскостью, параллельны между собой: α || β, α ∩ γ = а, β ∩ γ = b ⇒ a || b. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости: c ⊥ α, α || β ⇒ c ⊥ β . Две плоскости, перпендикулярные одной и той же прямой, параллельны: α ⊥ c, β ⊥ c ⇒ α || β . Плоскость, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости: γ ⊥ α, α || β ⇒ γ ⊥ β . |

