Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Владимирский государственный университет

имени Александра Григорьевича и Николая Григорьевича Столетовых»
Кафедра «Автомобильные дороги»

Отчет по практическим занятиям

по дисциплине «Теория упругости»

Выполнил:

студент гр. ЗСд-119

Мигунов М.М.

Принял:

Кондратьева Л. Е.

Владимир 2023 г.

Напряженное состояние (плоское напряженное состояние) в точке твердого тела задано компонентами






Найти

- главные напряжения в точке

- положения главных площадок

- наибольшие касательные напряжения.

Определение напряжений на наклонной площадке. Напряжения, действующие на наклонной площадке, находим по формулам (2.2а) и (2.2б). В этих формулах положение площадки задает угол между нормалью к площадке и осью . Этот угол нельзя путать с углом , указанным на рис. 2.3.

Можно отсчитывать угол  не от оси , а от осиz, но тогда в формулах (2.2а) и (2.2б) напряжения

---

, надо поменять местами и напряжение заменить напряжением . Надо выбирать более удобный способ.

Используем угол  между и осью , отсчитывая его от оси к нормали : . Значение угла положительное, так как угол отсчитывается против часовой стрелки.

Согласно (2.2а) и (2.2б)



,



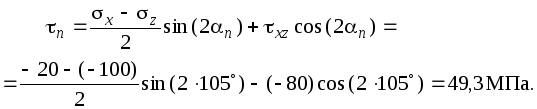
Получившееся нормальное напряжение  отрицательно, значит, оно направлено к площадке (сжимающее). Касательное напряжение положительно, это значит, что оно обходит площадку по часовой стрелке.

Используем теперь угол  между нормалью и осью , отсчитывая его отzк : . Формулы (2.2а) и (2.2б) записываем в измененном виде:

---

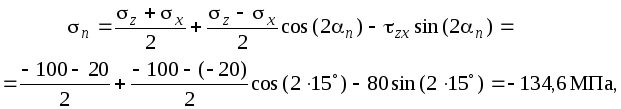
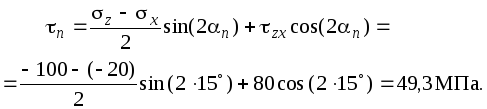
Рис. 1. Напряжения

на наклонной

площадке

Абсолютная величина полного напряжения (или просто полное напряжение)

Вычисленные напряжения показаны на рис.1.

Определение главных напряжений и главных направлений.Согласно (1) главные напряжения



.

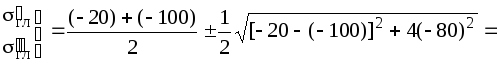
После вычисления главные напряжения следует пронумеровать согласно убыванию. Чтобы не путать напряжения до и после нумерации, специально используются для этих напряжений разные обозначения. Главные напряжения, пронумерованные согласно их величине,

, , .

Найдем положение главных площадок. Сказанное о способах вычисления напряжений по наклонной площадке относится и к способам вычисления положения главных площадок. Здесь мы вычислим углы  , , определяющие положения главных площадок, одним способом: будем отсчитывать эти углы от направления оси . Углы являются решениями уравнения (2.7):

,

то есть





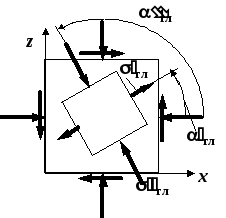
Рис. 2. Определение

положения главных

площадок

---

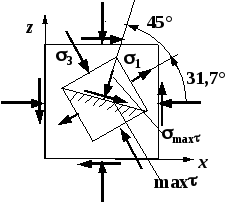
Рис. 3. Площадка

с максимальным

касательным напряжением

Получены два значения угла, которые отвечают площадкам с напряжениями , (рис. 2.). Выясним, какому из этих напряжений соответствует угол . Для этого определим по формуле (2.8) знак второй производной при :

.

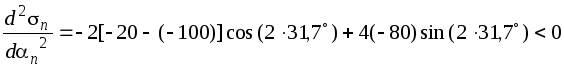Знак отрицательный, следовательно, по этой площадке действует бóльшее из найденных главных напряжений – напряжение . Теперь можно в соответствии с нумерацией главных напряжений пронумеровать и углы: , .

Определение максимального касательного напряжения.Касательное напряжение, максимальное среди касательных напряжений на площадках, перпендикулярных плоскости (рис. 3), определяется формулой (2.10):

МПа.

В рассматриваемом примере главные напряжения  , , поэтому касательное напряжение является максимальным среди касательных напряжений для всей совокупности площадок, проходящих через заданную точку: .

Нормальные напряжения на той же площадке даются формулой (2.11):

---

МПа.

Графический способ исследования напряженного состояния



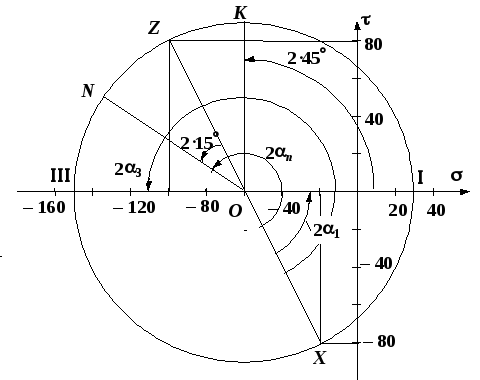
Рис. 4. Круг Мора, изображающий заданное

плоское напряженное состояние

Круг напряжений Мора является средством вычисления. При выполнении задачи его необходимо построить в крупном масштабе на миллиметровке, используя заточенный карандаш. Чем точнее выполнены построения, тем точнее будет получен результат.

Строим круг напряжений Мора (рис. 4). Изображаем систему координат с одинаковым масштабом по вертикальной и горизонтальной осям. Отмечаем на координатной плоскости две точки X, , соответствующие заданным площадкам с нормалями . Координатами точек X (160, -80),

Z (-70, 80) являются нормальные и касательные напряжения на заданных площадках. Соединяем точки отрезком, который представляет собой диаметр круга Мора. Точка О пересечения диаметра с осью – центр круга. Проводим окружность.

Точкам I, III пересечения круга с горизонтальной осью соответствуют главные площадки 1, 3. Горизонтальные координаты этих точек (измеренные в масштабе) являются главными напряжениями: МПа, МПа.

Углы  , , определяют положения главных площадок. Отмеченные на рисунке углы дают удвоенные значения , . По рисунку сразу видно, какому главному напряжению соответствует каждое значение угла. Графически найденные значения:

---

Смотрите также файлы

• Контрольная работа По дисциплине Метрология, стандартизация и сертификация.docx

• Февральская революция 1917 года.docx

• Лабораторная работа исследование разветвленных.pdf

• Зимующие такие птицы.docx

• 2. Образцы заданий для оценивания в 6 классе Задания для суммативного оценивания за 1 четверть.doc