Файл: Отчет по практическим занятиям по дисциплине Теория упругости.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,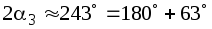 . Графический способ дает возможность проверить аналитическое решение, поэтому в расчетной работе следует рядом с кругом напряжений на отдельном рисунке показать положения главных площадок и напряжения на них.
. Графический способ дает возможность проверить аналитическое решение, поэтому в расчетной работе следует рядом с кругом напряжений на отдельном рисунке показать положения главных площадок и напряжения на них.
Площадке, по которой действует максимальное касательное напряжение, соответствует точка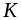 круга. Координаты точки
круга. Координаты точки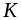 дают значения
дают значения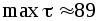 МПа,
МПа,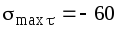 МПа.
МПа.
Найдем с помощью круга напряжений напряжения на наклонной площадке. Построим на круге точку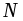 , соответствующую наклонной площадке. Для этого отложим от радиуса OX (соответствующего оси x)против часовой стрелки угол
, соответствующую наклонной площадке. Для этого отложим от радиуса OX (соответствующего оси x)против часовой стрелки угол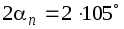 , либо от радиуса ОZ (соответствующего оси z) в том же направлении угол 215. Координаты точки
, либо от радиуса ОZ (соответствующего оси z) в том же направлении угол 215. Координаты точки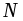 дают напряжения на наклонной площадке:
дают напряжения на наклонной площадке: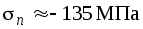 ,
,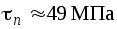 .
.
Полное представление о напряженном состоянии дают три круга напряжений. Точки каждого круга соответствуют площадкам, которые перпендикулярны одной из главных площадок. Круги строятся по главным напряжениям. Обычно изображение напряженного состояния в виде трех кругов Мора используется в качестве иллюстрации, а не в качестве способа вычисления, поэтому данный рисунок можно выполнить в меньшем масштабе и не обязательно на миллиметровке. Все три круга напряжений для рассматриваемого напряженного состояния показаны на рис. 5. Построенный на рис. 4 круг напряжений соответствует площадкам, перпендикулярным плоскости чертежа (перпендикулярным второй главной площадке). Из рис. 5 видно, что максимальное касательное напряжение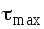 определяется по большему кругу.
определяется по большему кругу.
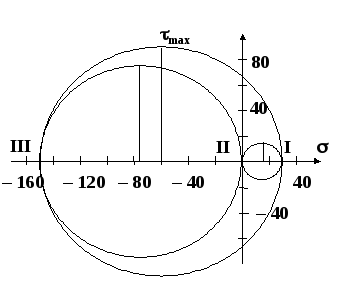
Рис. 5. Круги Мора,
изображающие объемное
напряженное состояние
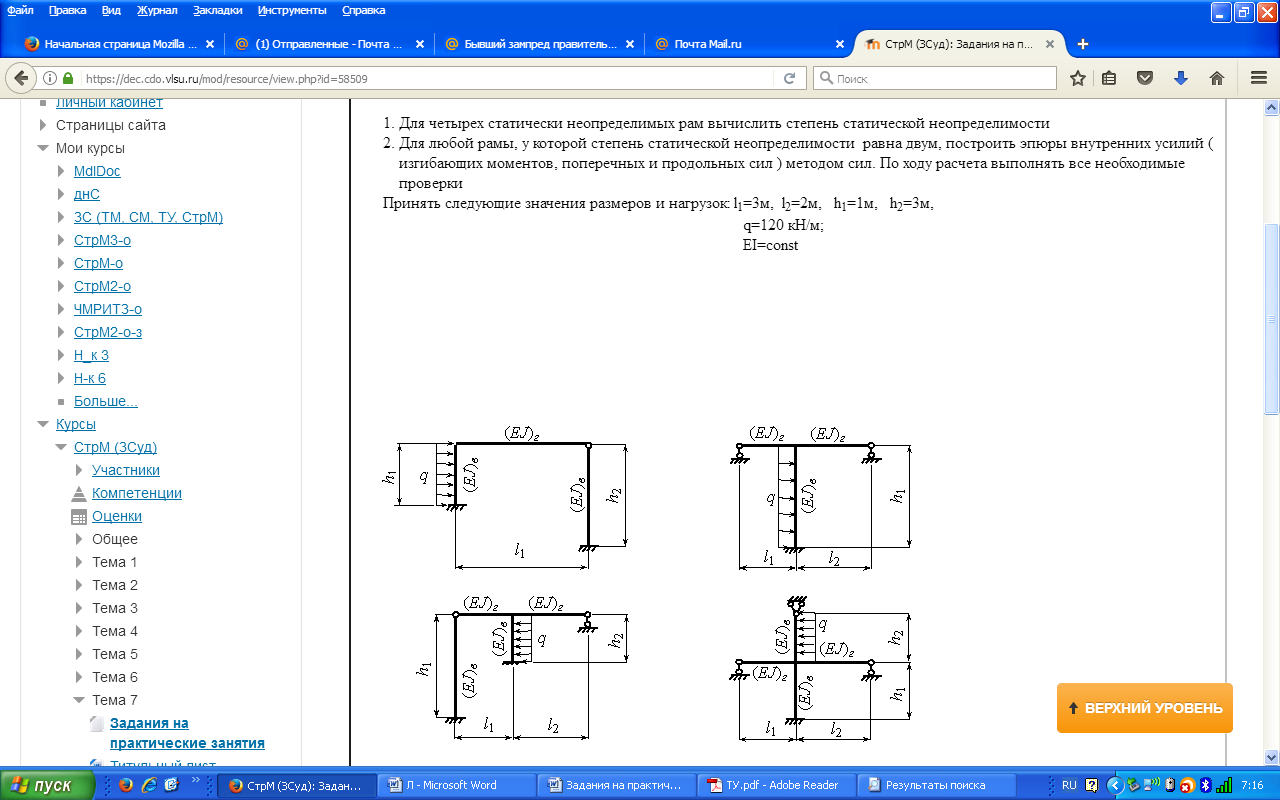
l1=3м, l2=2м, h1=1м, h2=3м, q=120 кН/м, EI=const.
Площадке, по которой действует максимальное касательное напряжение, соответствует точка
Найдем с помощью круга напряжений напряжения на наклонной площадке. Построим на круге точку
Полное представление о напряженном состоянии дают три круга напряжений. Точки каждого круга соответствуют площадкам, которые перпендикулярны одной из главных площадок. Круги строятся по главным напряжениям. Обычно изображение напряженного состояния в виде трех кругов Мора используется в качестве иллюстрации, а не в качестве способа вычисления, поэтому данный рисунок можно выполнить в меньшем масштабе и не обязательно на миллиметровке. Все три круга напряжений для рассматриваемого напряженного состояния показаны на рис. 5. Построенный на рис. 4 круг напряжений соответствует площадкам, перпендикулярным плоскости чертежа (перпендикулярным второй главной площадке). Из рис. 5 видно, что максимальное касательное напряжение

Рис. 5. Круги Мора,
изображающие объемное
напряженное состояние
-
Для четырех статически неопределимых систем вычислить степень статической неопределимости -
Для любой системы построить эпюры внутренних усилий
l1=3м, l2=2м, h1=1м, h2=3м, q=120 кН/м, EI=const.


