ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 127
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Гранулометрический состав грунта. Основные фракции частиц
Структурные связи между частицами грунта
Основные физические характеристики грунтов
Классификация глинистых грунтов:
Основные расчетные модели грунта
Водопроницаемость грунтов. Закон ламинарной фильтрации
Сопротивление грунтов сдвигу. Способы испытания грунтов на
Условие предельного равновесия грунтов
Определение напряжений в массиве грунтов. Распределение напряжений от собственного веса грунта
Определение напряжений от равномерно нагрузки, действующей по площади
Основные расчетные модели грунта
Выделяют общие принципы расчетов по предельным состояниям:
-по несущей способности (потеря устойчивости, хрупкое, вязкое или иного характера разрушение грунта, чрезмерные пластические деформации или деформации ползучести…)
-по деформациям (достижение состояния, затрудняющего нормальную эксплуатацию сооружения или снижающего его долговечность вследствие недопустимых перемещений – осадок, кренов…)
Сущность расчетов предельных состояний заключается в том, что:
-
по первой группе: расчетная нагрузка на основание не должна превышать силу предельного сопротивления грунтов основания -
по второй группе: совместная деформация сооружений и основания не должна превышать предельного значения для конструктивной схемы данного сооружения.
Модель теории линейного деформирования грунта
Используется для расчетов конечных напряжений и стабилизированных осадок.
Базируется на предположении, что при однократном нагружении зависимость между
напряжениями и деформациями в грунтах линейна. При нагружении рассматривается лишь общая деформация грунта без разделения ее на упругую и пластическую. Первое допущение
обеспечивает возможность использования для расчетов напряжений грунта аппарата теории
упругости, а второе - при известных напряжениях рассчитывать конечные деформации оснований Модель теории фильтрационной консолидации
Используется для расчетов развития осадок во времени.
Принимается, что полное напряжение, возникающее в грунте от приложенной нагрузки,
разделяется на напряжение в скелете грунта (эффективное напряжение) и напряжение в поровой воде (поровое давление).
В различных точках массива грунта под действием нагрузки возникают разные значения порового давления. Вследствие этого образуется разность напоров в поровой воде и происходит ее отжатие в менее нагруженные области массива. Одновременно под действием эффективных напряжений происходит перекомпановка частиц и уплотнение грунта
Модель теории предельного напряженного состояния грунта
Используется для расчетов несущей способности, прочности, устойчивости и давления грунтов на ограждения.
Рассматривает только предельное состояние грунта, т.е. такое напряженное состояние, когда в массиве грунта от действующих нагрузок сформировались значительные по размерам
замкнутые области, в каждой точке которых устанавливается состояние предельного равновесия. Поэтому теорию предельного напряженного состояния часто называют теорией предельного равновесия
-
Механические свойства грунтов. Компрессионная зависимость
Механические свойства грунтов – это их способность сопротивляться изменению объема и формы в результате физических воздействий
Различают свойства грунтов
-
Деформационные способность грунта сопротивляться развитию деформаций -
Прочностные способность грунта сопротивляться разрушению -
Фильтрационные способность грунта пропускать и отжимать воду из пор под действием нагрузки
Механические свойства грунтов определяются в соответствии с ГОСТами. ГОСТ 12248 и др Компрессионная зависимость
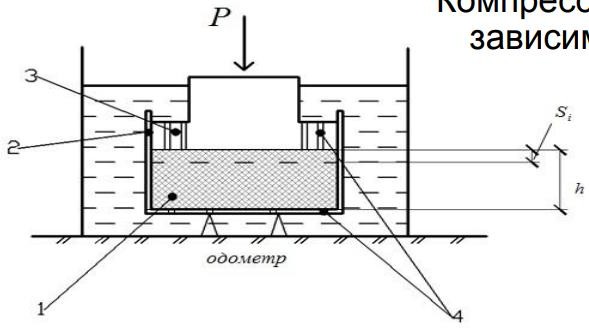
Полностью водонасыщенный образец грунта(1) помещают в
кольцо(2) и с помощью
поршня(3) прикладывают силу Р. Сжатие образца в одометре происходит за счет уменьшения объема пор ????пори отжатия воды через отверстия(4)
∆???? =
∆????пор

????
= ???? ∙ ????????
 ???? ∙ ℎ
???? ∙ ℎ= ????????
 ℎ
ℎИзменение пористости
????????
???? = ???? − (1 + ???? )
???? 0 0 ℎ
???????? – текущий коэффициент пористости А – площадь сечения, м2
????
 ???? =
???? =ℎ
h – первоначальная высота образца, мм
????0 – начальный коэффициент пористости
S – осадка грунта, мм
???? – относительная деформация сжатия
-
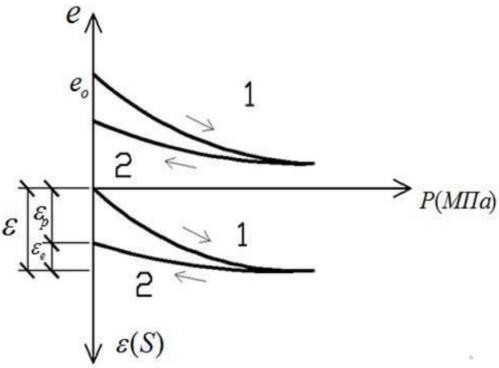
Компрессионная ветвь при приложении нагрузки отображает уменьшение пористости при возрастании нагрузки -
Декомпрессионная ветвь после удаления нагрузки отображает обратный процесс -
увеличение объема (V) т е набухание
Расположение ветви набухания ниже ветви сжатия свидетельствует о том что грунт обладает значительной остаточной (пластической) ???????? деформацией
Ветвь набухания обусловлена упругими деформациями ????????
???????? – упругая деформация
???????? – остаточная или пластическая деформация
???? – общая деформация
- 1 2 3 4 5 6 7 8 9 ... 14
Структурная прочность грунта
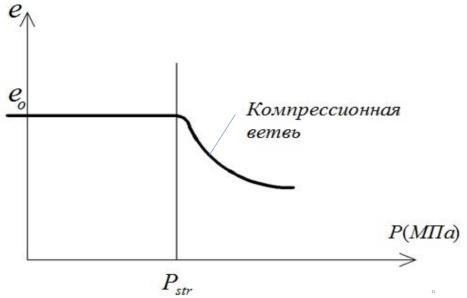
Многие грунты природного сложения, кроме скальных могут быть уплотнены, что
сопровождается возникновением в них хрупких кристаллизационных связей. Эти связи придают грунты некоторую прочность, которая называется структурной прочностью грунта.
При ???? < ???????????????? процесс уплотнения в грунте практически не развивается При ???? > ???????????????? происходит резкое уплотнение или разрушение грунта
Структурную прочность иногда используют для ограничения мощности сжимаемой толщи под подножием фундамента, полагая, что при напряжениях в основании не превышающих ???????????????? уплотнение грунта не происходит.
-
Способы определения модуля деформации грунта (с помощью
компрессионной кривой, испытанием статической нагрузкой, при помощи прессиометра)
Модуль деформации грунта - величина, характеризующая зависимость осадки от нагрузки
В качестве деформационной характеристики зависимости между напряжениями и деформациями используют модуль деформации Е, который является основной деформационной характеристикой
Определение модуля деформации с помощью компрессионной кривой

 ???? = ∆???? ∙ ℎ ∙ ????;???? = ???? (1+????0)
???? = ∆???? ∙ ℎ ∙ ????;???? = ???? (1+????0)∆????
????0
∆???? – приращение
нагрузки, Мпа
∆???? – приращение осадки, мм
h – первоначальная высота образца, мм
???? – коэффициент бокового расширения грунта.
Испытание статической нагрузкой
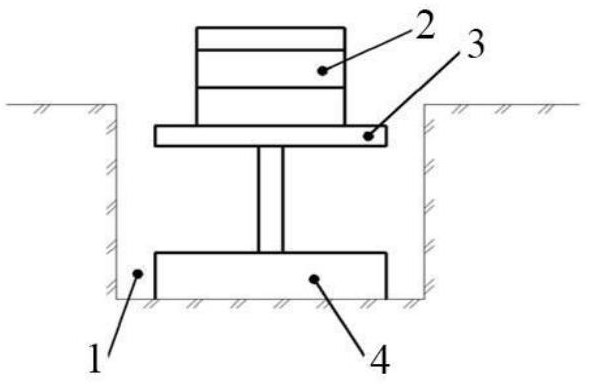
На дно шурфа(1) устанавливают штамп(4), к платформе(3) прикладывают ступенями нагрузку(2) и фиксируют осадку грунта
Шурф – жто углубление в грунте Формула Шлейхера
 ???? = ???? ∙ ????(1 − ????2) ∆????
???? = ???? ∙ ????(1 − ????2) ∆????∆????
???? – коэффициент, для круглых штампов равен 0,8
d – диаметр штампа, мм
V – коэффициент Пуассона
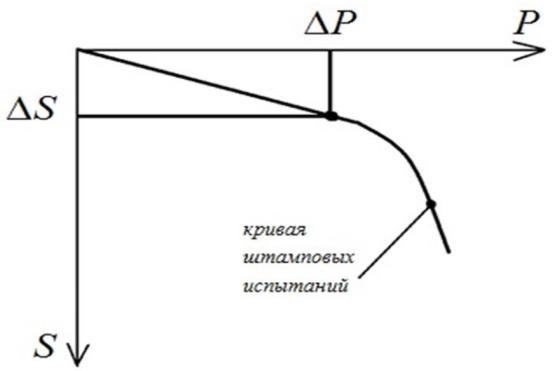
При помощи прессиометра
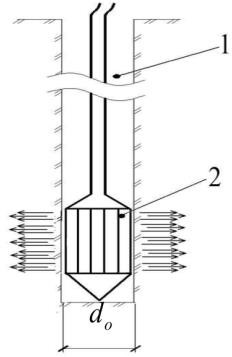
В скважину(1) опускают цилиндрический резиновый баллон заполненный жидкостью т.е
прессиометр(2). Давление жидкости в баллоне увеличивают оно передается на стенки скважины и уплотняет окружающий грунт. С помощью датчиков фиксируется давление и деформация грунта
∆????
 ???? = ∆???? ∙ (1 + ????)????0
???? = ∆???? ∙ (1 + ????)????0Применяется только для изотропных грунтов, когда свойства грунтов во всех направлениях одинаковы
- 1 2 3 4 5 6 7 8 9 ... 14

