ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 7
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание №
по учебному курсу « Теоретическая механика »
(наименование учебного курса)
Вариант П-9; Г-6; С-10 (при наличии)
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Бланк выполнения задания 3
| 1. Записываются данные задания |
| Коленчатый вал весом Р=13 кН с центром масс в точке С закреплен на подшипниках А и О. Колена вала расположены во взаимно перпендикулярных плоскостях. Силы 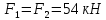 приложены в серединах колен соответственно в точках Т и W, направлены под углами приложены в серединах колен соответственно в точках Т и W, направлены под углами 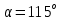 к плоскости хОу и к плоскости хОу и 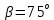 к вертикальной плоскости уОz. к вертикальной плоскости уОz.Найти реакции в опорах А и О, а так же силу 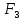 , которая паралелльна плоскости хОz и приложена в точке T, если угол наклона к прямой, параллельной оси Оz , которая паралелльна плоскости хОz и приложена в точке T, если угол наклона к прямой, параллельной оси Оz 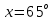 равен и равен и 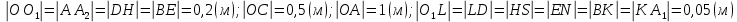 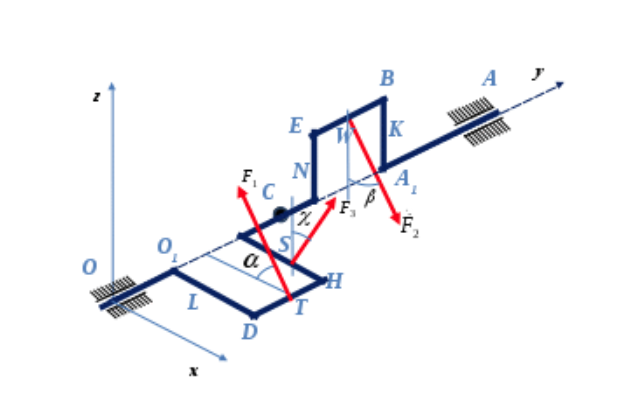 |
2. Рисунок, на котором показаны все реакции
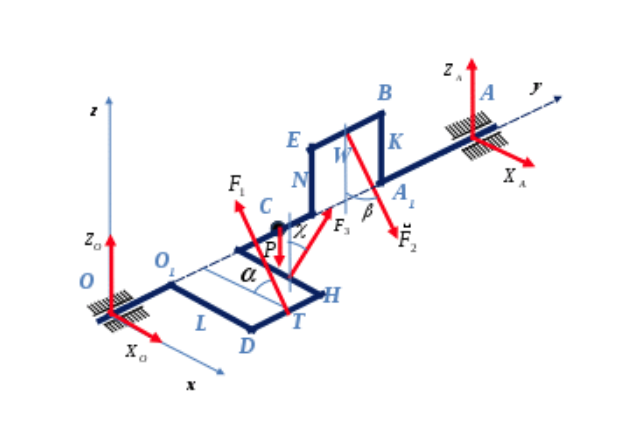
| 3. Записываются уравнения равновесия | ||
| Рассмотрим равновесие вала. На вал действуют заданные силы F1, F2, сила тяжести вала P, приложенная к точке С и неизвестная сила F3. Освободим вал от связей и приложим к нему реакции связей. XA, ZA – составляющие реакции цилиндрического подшипника А, расположенные в плоскости, перпендикулярной оси подшипника. X0, Z0 - составляющие реакции цилиндрического подшипника О, расположенные в плоскости, перпендикулярной оси подшипника.
| ||
| 4. Решаются уравнения равновесия | ||
| Из уравнения (4) получаем: 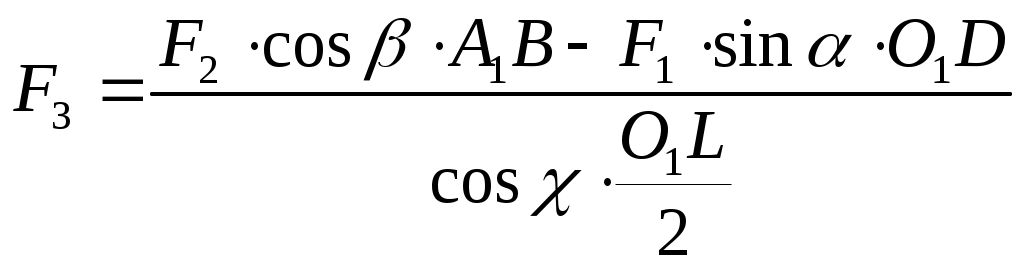 Из уравнения (5) Из уравнения (3) Из уравнения (2) Из уравнения (1) получим | ||
| 5. Записывается ответ | ||
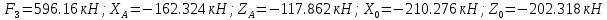 |

