ЛАБОРАТОРНАЯ РАБОТА

Вариант 37

Задание.

1. Из приложения взять выборку объема n=200. Выборку произвести серийным способом с номера, указанного преподавателем.

2. По выборке найти статистические оценки математического ожидания и среднего квадратического отклонения.

3. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона при уровне значимости  = 0,05.

4. Построить гистограмму опытных данных.

Таблица 1

Долговечность деталей, час.

926	888	568	933	794	741	972	824	832	1008
790	723	915	840	928	640	710	1093	629	690
848	812	546	706	836	775	1034	974	860	1075
1103	821	1040	1074	955	648	578	554	857	541
732	577	707	998	846	710	943	904	718	790
777	705	660	1153	1084	1172	883	870	811	1098
775	413	775	525	688	967	875	503	843	728
1054	970	799	781	1120	600	797	1240	510	908
717	973	866	938	786	921	610	690	785	986
502	405	1030	651	380	789	1058	1201	1024	803
627	329	405	756	947	961	830	840	1080	615
690	855	790	1011	985	596	723	1169	708	823
963	743	766	953	551	678	525	563	570	543
873	685	831	856	752	753	1003	1210	872	709
430	496	520	768	794	698	946	583	794	780
1180	609	671	1045	919	742	806	930	900	625
864	785	525	1023	520	765	589	903	403	764
796	1164	715	818	800	661	618	880	739	810
931	696	775	802	926	726	256	727	620	775
840	347	725	1132	809	930	1302	1142	1062	932

---

Решение:

Случайную величину (долговечность детали) обозначим Х. Найдем из таблицы 1 .

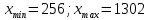Весь интервал, в которые попали статистические данные, разбиваем на ряд частичных интервалов.



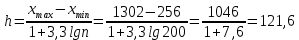
Нам удобно взять h=122

Левая границы первого интервала:



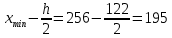
Подсчет числа опытных данных n_i, попавших в i-тый частичный интервал, приведен в табл.2.

Таблица 2

Число опытных данных, попавших в частичные интервалы

№ п/п	Интервалы	Подсчет опытных данных	n	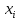– середины интервалов
1	195 – 317		1	256
2	317 – 439		8	378
3	439 – 561		14	500
4	561 – 683		24	622
5	683 – 805		59	744
6	805 – 927		41	866
7	927 – 1049		31	988
8	1049 – 1171		16	1110
9	1171 – 1293		5	1232
10	1293 – 1415		1	1354
∑	-	-	200	-

---

2. 
   По выборке определим оценки параметров нормального распределения.
   

Выборочное среднее:





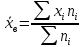
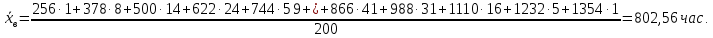
Исправленная дисперсия:





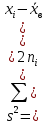
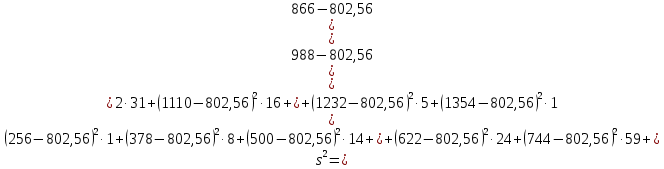
Исправленное среднее квадратическое отклонение:

2. 
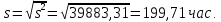
   Найдем теоретическое число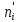 , попавшее в i – тый интервал согласно нормальному закону распределения.
   

Пронормируем X, т.е перейдем к случайной величине:



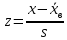
и вычислить концы интервала:



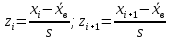
Причем наименьшее значение z, т. е. z₁ полагают равным -∞, а наибольшее, т. е. z_k+1, полагают равным ∞.

Теоретические частоты вычислим по формуле:



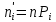
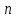– объем выборки (сумм всех частот)

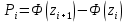– вероятности попадания X в интервалы .

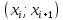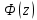– функция Лапласа

Расчет 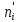приведен в таблице 3.

Таблица 3

Теоретическое число

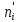
№ п/п	Границы интервала			Границы интервала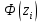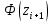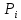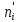
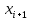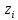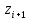1	195	317	- ∞		-2,43	-0,5	-0,4925		0,0075		1,5
2	317	439	-2,43		-1,82	-0,4925	-0,4657		0,0268		5,4
3	439	561	-1,82		-1,21	-0,4657	-0,3868		0,0789		15,8
4	561	683	-1,21		-0,60	-0,3868	-0,2253		0,1615		32,3
5	683	805	-0,60		0,01	-0,2253	0,0049		0,2302		46,0
6	805	927	0,01		0,62	0,0049	0,2334		0,2285		45,7
7	927	1049	0,62		1,23	0,2334	0,3914		0,1580		31,6
8	1049	1171	1,23		1,84	0,3914	0,4675		0,0761		15,2
9	1171	1293	1,84		2,46	0,4675	0,4930		0,0255		5,1
10	1293	1415	2,46		+∞	0,4930	0,5		0,0070		1,4
∑	-	-	-		-	-	-		1		200

---

Проверим согласие нормального закона по критерию Пирсона при уровне значимости α=0,05. Расчет 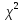сведен в таблице 4. Значения 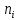взяты из таблицы 2, а - из таблицы 3.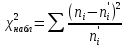



Интервалы, содержащие малочисленные эмпирические частоты (n_i<5), сложим.

Таблица 4

Нахождение

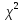
№ п/п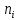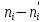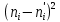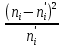
1	1	1,5	2,1	4,5	0,7
2	8	5,4
3	14	15,8	-1,8	3,2	0,20
4	24	32,3	-8,3	68,8	2,13
5	59	46,0	13,0	168,1	3,65
6	41	45,7	-4,7	22,1	0,48
7	31	31,6	-0,6	0,4	0,01
8	16	15,2	0,8	0,6	0,04
9	5	5,1	-0,5	0,3	0,00
10	1	1,4
∑	200	200	-	-	7,22

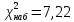
По таблице критических значений

---

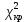при уровне значимости 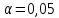и числе степеней свободы k = l – 3= 8– 3 =5 (l– число интервалов)найдем: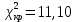



Так как 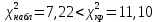, то нулевую гипотезу о нормальном распределении принимаем на данном уровне значимости, т. е. нормальный закон распределения согласуется с опытными данными.

2. 
   Построим гистограмму опытных данных.
   

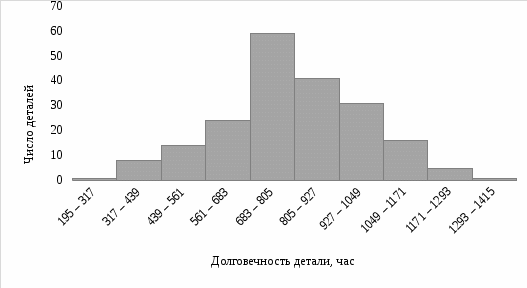
Рисунок 1. Гистограмма распределения деталей по долговечности

---

Смотрите также файлы

• Морали, но не все моральные нормы становятся.pdf

• Приобретение знаний о роли физической культуры в обеспечении здоровья, формирование умений применять полученные знания.docx

• Программа реабилитации или абилитации инвалида, выдаваемая федеральными государственными учреждениями медикосоциальной экспертизы.docx

• Лабораторная работа 2 Разработка моделей представления знаний в информационной среде их сопровождения Фамилия Денисенко.docx

• Кнтізбеліктаырыпты жоспар Дене шынытыру пні 8 Асынып Барлыы 102 саат, аптасына 3 саат.docx